3. Формула полной вероятности. Формула Бейеса.

Разделы литературы: [1] гл.4, §2, 3; [2] гл.2, §3, 4.

Вероятность события A, которое может наступить лишь при условии появления одного из несовместных событий H₁, H₂, ..., H_n, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A.

.

(7)

Эта формула называется формулой полной вероятности. События H₁, H₂, ..., H_n часто называют «гипотезами».

Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формулам Бейеса

.

(8)

Пример 5. В магазин поступили электрические лампочки одного типа, изготовленные на четырех ламповых заводах: с 1-го завода 250 шт., со 2-го – 525 шт., с 3-го – 275 шт. и с 4-го – 950 шт. Вероятность того, что лампочка прогорит более 1500 часов, для 1-го завода равна 0,15, для 2-го – 0,30, для 3-го – 0,20, для 4-го – 0,10. При раскладке по полкам магазина лампочки были перемешаны.

а) Какова вероятность того, что купленная лампочка прогорит более 1500 часов?

б) Купленная лампочка прогорела более 1500 часов. С какой вероятностью она была изготовлена 1-м заводом?

Решение.

а) Пусть A – событие, состоящее в том, что купленная лампочка прогорит более 1500 часов. Лампочка может быть изготовлена любым из четырёх заводов, поэтому возможны 4 гипотезы Н₁ – лампочка изготовлена 1-м заводом, Н₂, Н₃ и Н₄ – изготовлена соответственно 2-м, 3-м или 4-м заводом. Так как всего лампочек 250+525+275+950=2000 шт., то вероятности гипотез соответственно равны:

; ;;.

Условная вероятность того, что лампочка, изготовленная 1-м заводом, прогорит более 1500 часов равна . Условная вероятность того, что лампочка, изготовленная 2-м заводом, прогорит более 1500 часов равна. Аналогичнои(это следует из условия задачи).

Используя формулу полной вероятности, имеем

.

б) Так как событие А уже произошло, то искомую вероятность найдём по формуле Бейеса, т.е. переоценим вероятность гипотезы Н₁:

.

Ответ: а) вероятность того, что лампочка прогорит более 1500 часов равна 0,1725;

б) вероятность того, что лампа, прогоревшая 1500 часов, изготовлена 1-м заводом равна 0,11.

4, 5. Повторение испытаний.

Надо знать: независимые испытания (испытания Бернулли), формулы Бернулли и свойства вероятностей Бернулли, приближенные формулы для вероятностей Бернулли (формулы Муавра-Лапласа и Пуассона) и условия их применения. Надо уметь пользоваться таблицей значений функции Лапласа.

Разделы литературы: [1] гл.5, §1-3; [2] гл.3, §1,2.

Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0 < p < 1), событие наступит ровно k раз, равна

,

(9)

где q = 1 – p.

Если число независимых испытаний велико, то формулу Бернулли применять (технически) достаточно сложно. В этих случаях применяют локальную теорему Лапласа. Вероятности того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0 < p < 1), событие наступит ровно k раз, приближенно равна

,

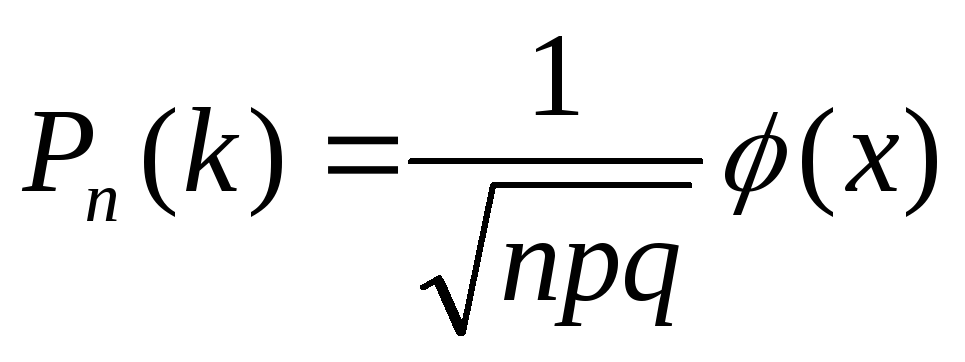(10)

где .

Функция обладает следующими свойствами:

1) функция является чётной, то есть;

2) функции монотонно убывает при положительных значениях аргумента;

3) для всех значений x > 5 значение функции .

Интегральная теорема Лапласа. Вероятности того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0 < p < 1), событие наступит не менее k₁ раз и не более k₂ раз, приближенно равна

,

(11)

где , .

Функция обладает следующими свойствами:

1) функция является нечетной, то есть;

2) функции – монотонно возрастающая;

3) для всех значений x > 5 значение функции .

Примечание.Таблицы значений функций иможно найти в приложениях любого учебника по теории вероятностей.

Пример 6. Вероятность того, что стрелок при одном выстреле попадет в мишень равна 0,8. Стрелок произвел 5 выстрелов. Найти вероятность того, что:

а) стрелок попадёт ровно 3 раза;

б) стрелок попадёт более 3 раз;

в) стрелок попадёт не менее 3 раз;

г) стрелок попадёт менее 3 раз.

Решение.

По условию имеем: n = 5 – число испытаний в эксперименте (число выстрелов), p = 0,8 – вероятность «успеха», q = 1 – p = 1 – 0,8 = 0,2 – вероятность «неудачи».

а) k = 3. Найти вероятность .

Так как число испытаний мало, то воспользуемся формулой Бернулли.

.

б) k > 3. Найти вероятность . Также воспользуемся формулой Бернулли.

.

в) k ≥ 3. Найти вероятность .

.

г) k < 3. Найти вероятность .

.

Ответ: а) 0,2048; б) 0,74; в) 0,94; г) 0,058.

Пример 7. В каждом из 700 независимых испытаний событие А происходит с постоянной вероятностью 0,35. Найти вероятность того, что событие А происходит:

а) точно 270 раз;

б) не меньше чем 230 раз и не больше чем 270;

в) больше чем 270 раз.

Решение.

Так как количество испытаний довольно велико, а вероятность не очень мала, то для вычисления искомых вероятностей можно использовать локальную и интегральную теоремы Лапласа.

a) Дано n = 700, p = 0,35, k = 270. Найти вероятность .

Воспользуемся локальной теоремой Лапласа. Подставляя исходные данные в формулу (10), получим

,

.

По таблице найдем значение функции .

Тогда искомая вероятность .

б) Дано: n = 700, p = 0,35, k₁ = 230, k₂ = 270. Найти вероятность . Воспользуемся интегральной теоремой Лапласа

Подставляя исходные данные в формулу (11), найдем

,

.

По таблице найдём значения функций:

, .

Тогда искомая вероятность равна

.

в) Дано: n = 700, p = 0,35, k > 270. Найти вероятность .

Для нахождения указанной вероятности также воспользуемся формулой (11). Так как k строго больше 270, то k₁ = 271, а всего испытаний 700, поэтому k₂ = 700.

Подставляя исходные данные, найдем

,

.

По таблице найдём значения функций:

, .

Тогда искомая вероятность равна

.

Ответ: а) 0,0045; б) 0,8591; в) 0,0197.