6. Дискретные случайные величины.

Надо знать: дискретная случайная величина (с.в.), законы распределения с.в., ряд распределения и функция распределения с.в., математическое ожидание и дисперсия дискретной с.в. – определение, смысл и свойства.

Разделы литературы: [1] гл.6, §1-8, гл. 7, §1-5, гл.8, §1-7; [2] гл.4, §1-3.

Законом распределения дискретной случайной величины называется соответствие между возможными значениями x₁, x₂, …, x_n этой случайной величины и соответствующими им вероятностями p₁, p₂, …, p_n.

Закон распределения дискретной случайной величины может быть задан таблично или аналитически, то есть с помощью формул.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности:

(12)

Математическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления события в одном испытании:

M(X) = n·p.

(13)

Дисперсией случайной величины X называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

(14)

Дисперсию удобно вычислять по формуле

(15)

Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и не появления события в одном испытании:

D(X) = n·p·q.

(16)

Пример 8. Стрелок производит три выстрела в цель. Вероятность попадания в цель при каждом выстреле равна 0,2. Составить закон распределения случайной величины X – числа попаданий в цель. Найти математическое ожидание M(X), дисперсию D(X).

Решение.

Случайная величина X может принимать следующие значения: x₁=0, x₂=1, x₃=2, x₄=3.

Для составления закона распределения случайной величины X найдем вероятности того, что случайная величина X примет соответствующие значения. В данной задаче испытания проводятся по схеме Бернулли. Действительно, число испытаний конечно. Каждое испытание является независимым. В каждом испытании наблюдается либо «успех» (попал в цель), либо «неуспех» (не попал в цель или промахнулся). Вероятность удачи в каждом испытании постоянна. Поэтому можно утверждать, что случайная величина X имеет биномиальное распределение и соответствующие вероятности вычисляются по формуле Бернулли:

Найдём их:

Тогда искомый закон распределения примет вид

X	0	1	2	3
p	0,512	0,384	0,096	0,008

Убедимся, что сумма вероятностей равна единице:

0,512 + 0,384 + 0,096 + 0,008 = 1.

Так как с.в. имеет биномиальный закон распределения, то M(X) = n·p = 3·0,2 = 0,6 и D(X) = n·p·q = 3·0,2·0,8 = 0,48.

Пример 9. Среди 9 изделий 6 – изделия высшего сорта. Наудачу выбрали три изделия. Случайная величина X – число изделий высшего сорта среди выбранных трех изделий. Составить закон распределения случайной величины X. Найти математическое ожидание M(X), дисперсию D(X).

Решение.

Так как из 9 изделий 6 высшего сорта и выбирается из них 3 изделия, то случайная величина X может принимать следующие значения: .

В данном примере с.в. X имеет гипергеометрическое распределение. Вероятности того, что случайная величина X примет соответствующие значения найдем по формуле 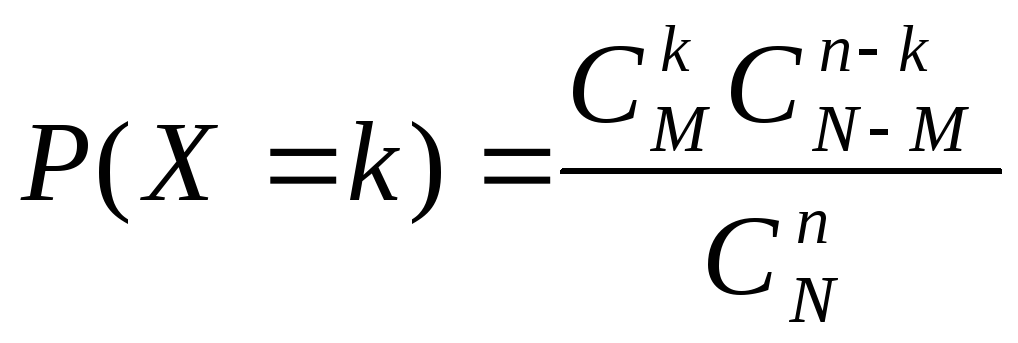. В нашем случаеN = 9, n = 6, M = 3. Предварительно вычислим число сочетаний из 9 по 3 (число способов которыми можно из 9 изделий извлечь 3):