7. Непрерывные случайные величины.

Надо знать: функция распределения и плотность непрерывных случайных величин и их свойства; характеристики непрерывных случайных величин.

Разделы литературы: [1] гл.10, §1-3, гл. 11, §1-3, гл.12, §1; [2] гл.6, §1-3.

Пример 10. Случайная величина задана интегральной функцией F(x). Найти дифференциальную функцию f(x) (функцию плотности), математическое ожидание, дисперсию, построить графики.

Решение.

По определению плотность распределения вероятностей непрерывной случайной величины есть первая производная от функции распределения:

Найдем математическое ожидание случайной величины X. Так как случайная величина X является непрерывной, то ее математическое ожидание найдем по формуле

.

.

Найдем дисперсию случайной величины X по формуле (16). Для этого найдём математическое ожидание квадрата с.в. X

.

.

Тогда дисперсия .

Графики дифференциальной и интегральной функций:

8. Нормальное распределение.

Надо знать: определение нормального распределения и смысл его параметров; график плотности нормального распределения; свойства нормального распределения, правило трех сигм.

Разделы литературы: [1] гл.12, §2-7; [2] гл.6, §5.

Пример 11. Фасовка муки происходит автоматически. По стандарту масса мешка должна отклонятся от 25 кг не более чем на 0,05кг. Найти среднее квадратическое отклонение, если 6% мешков имеют нестандартную массу. Предполагается, что массы мешков распределены по нормальному закону.

Решение.

По условию задачи 6% мешков имеют нестандартную массу, следовательно, 94% мешков стандартной массы. Значит, вероятность того, что отклонение с.в. от математического ожидания а = 25 по абсолютной величине меньше равна ,0,94.

Так как , то,. По таблице значений функцииФ(x) находим что . Следовательно,. Откуда=0,05/1,88=0,03.

Ответ: =0,03.

Математическая статистика

9. Статистическое распределение выборки. Эмпирическая функция распределения. Полигон и гистограмма. Числовые характеристики выборки.

Разделы литературы: [1] гл.15, §6-8,гл. 16; [2] гл.9, §1-3, гл.10, §1.

Пример 12. Путем опроса получено значений признакаX.

6	9	5	1	8	1	2	5	3	6	9	8	5	2	3	6	7
2	5	8	4	6	9	4	8	5	7	3	6	4	2	5	6	4
7	8	5	9	9	1	2	4	1	6	9	5	1	8	1	2

Требуется:

1. построить дискретный и интервальный вариационные ряды распределения частот и относительных частот наблюдаемых значений X;

2. построить полигон и гистограмму относительных частот X;

3. найти эмпирическую функцию распределения и построить ее график;

4. вычислить числовые характеристики выборки: выборочное среднее 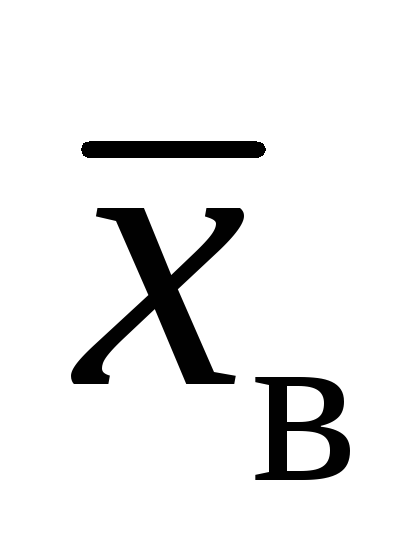; выборочнуюи исправленную дисперсию; выборочное среднее квадратическое отклонение.

Решение.

1) Для составления дискретного вариационного ряда отсортируем данные опроса по величине и расположим их в порядке возрастания

1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 4 4 4 4 4 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 7 7 7 8 8 8 8 8 8 9 9 9 9 9 9

Примечание.Указанную процедуру, как и большинство расчетов по математической статистике, можно выполнять, используя электронные таблицы, например, Microsoft Excel.

Посчитаем сколько раз встречается каждое из наблюдаемых значений признака X. Эти данные можно представить в виде статистического распределения выборки (в виде таблицы, в которой первая строка – варианты (наблюдаемые значение), вторая строка – частоты появления этих вариант). Найдём относительные частоты , гдеn – объём выборки, которые будем вычислять с одинаковой точностью.

Дискретный ряд распределения частот (n_i) и относительных частот ().

Таблица 1

	1	2	3	4	5	6	7	8	9
ni	6	6	3	5	8	7	3	6	6	50
	0,12	0,12	0,06	0,1	0,16	0,14	0,06	0,12	0,12	1

Для построения интервального вариационного ряда разобьём выборку, например, на 4 интервала. Вычислим шаг . Для каждого частичного интервала найдём сумму частот вариант, попавших в интервал. Найдём относительные частоты.

Таблица 2

Частичный интервал	Сумма частот вариант интервала ni	Относительные частоты wi	Плотность относительной частоты wi/h
1-3	15	0,3	0,15
3-5	13	0,26	0,13
5-7	10	0,2	0,1
7-9	12	0,24	0,12
	50	1

2) Полигон относительных частот – ломаная линия, соединяющая точки с координатами .

Гистограмма – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению (). Для построения гистограммы относительных частот найдём плотности относительных частот(см. 3-й столбец в таблице 2). На оси абсцисс отложим частичные интервалы, а над ними проведём отрезки, параллельные оси абсцисс на расстоянии.

3) Эмпирическую функцию распределения найдем, используя следующую формулу:

Для нашего примера

Эмпирическая функция распределения:

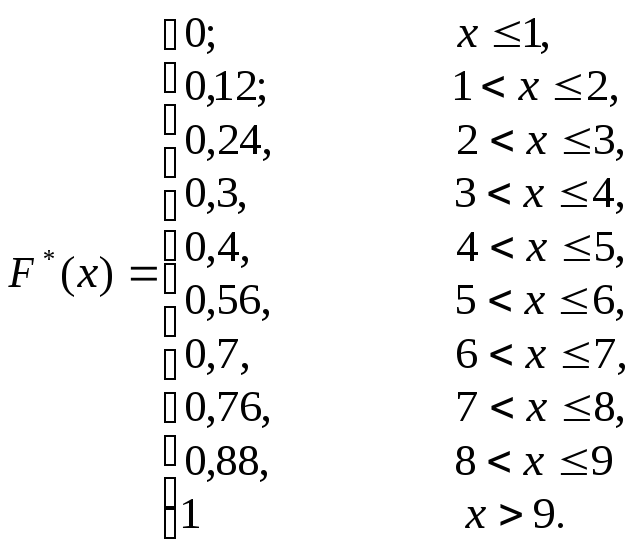
График эмпирической функции распределения:

4) Найдем основные числовые характеристики вариационного ряда: для этого составим расчётную таблицу:

	ni
1	6	6	16,3216	97,9296
2	6	12	9,2416	55,4496
3	3	9	4,1616	12,4848
4	5	20	1,0816	5,408
5	8	40	0,0016	0,0128
6	7	42	0,9216	6,4512
7	3	21	3,8416	11,5248
8	6	48	8,7616	52,5696
9	6	54	15,6816	94,0896
Сумма	50	252		335,92

Выборочное среднее найдем как среднее арифметическое взвешенное

Величина характеризует среднее значение признакаX.

Выборочная дисперсия

Исправленная дисперсия

Выборочное среднее квадратическое отклонение

.

Среднее квадратическое отклонение описывает абсолютный разброс значений показателя X и в данном случае составляет 2,6.