2. Свойства энтропии

1. Как следует из формулы (4.4), только в двух случаях:

• когда вероятность какого-либо исхода равна 1, поэтому вероятности остальных исходов равны 0, то есть один из исходов достоверен, поэтому общий итог опыта перестает быть случайным;

• все , то есть никакие из рассматриваемых исходов опыта невозможны. Во всех остальных случаях .

2. Очевидным следствием формулы (4.1) будет утверждение, что для двух независимых опытов и

. (4.5)

Энтропия сложного опыта, состоящего из нескольких независимых опытов, равна сумме энтропий отдельных опытов.

Приведем доказательство формулы (4.5).

Пусть опыт имеет исходов , , …, , которые реализуются с вероятностями , , …, , а опыт имеет исходов , , …, с вероятностями , , …, . Сложный опыт имеет исходов типа , где , . Поэтому (см. (4.4)):

. (4.6)

Поскольку опыты инезависимы, то независимыми окажутся события в любой паре. Поэтому:

, на основании чего

Таким образом, формулу (4.6) перепишем так:

;

;

.

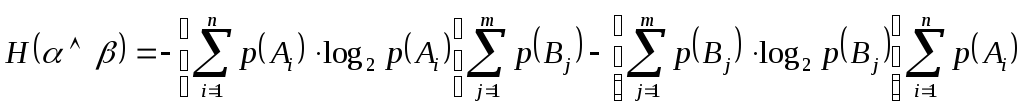Известно, что по условию нормировки вероятностей

и ,

Из формулы (4.4) следует, что

и .

Поэтому окончательно имеем:

,

что и требовалось доказать.

Теперь рассмотрим ситуацию, когда имеются два опыта с одинаковым числом исходов , в одном случае () они равновероятны, а в другом () – нет. Каково соотношение энтропий этих опытов? Примем без доказательства следующее утверждение:

. (4.7)

При прочих равных условиях наибольшую энтропию имеет опыт с равновероятными исходами.

Другими словами, энтропия максимальна в опытах, где все исходы равновероятны.

Кстати, результат, полученный в рассмотренном выше примере 1, иллюстрирует справедливость формулы (4.7).

Здесь усматривается аналогия (имеющая глубинную первооснову!) с понятием энтропии, используемым в физике. Впервые понятие энтропии было введено в 1865 году немецким физиком Рудольфом Клаузиусом: энтропия – это функция состояния термодинамической системы, описывающая направленность самопроизвольных процессов в системе. Клаузиус сформулировал II начало термодинамики. В частности, он показал, что энтропия достигает максимума в состоянии равновесия системы. Позднее, в 1872 году Людвиг Больцман, развивая статистическую теорию, связал энтропию системы с вероятностью ее (системы) состояния, дал статистическое (вероятностное) толкование II-му началу теормодинамики. В частности, Больцман показал, что вероятность максимальна у полностью разупорядоченной (равновесной) системы (аналогия с опытом, имеющим равновероятные исходы). Энтропия и термодинамическая вероятность тоже связаны логарифмической зависимостью. В физике энтропия  мера беспорядка в системе. При этом беспорядок понимается как отсутствие знания о характеристиках объекта (например, координат и скорости молекулы газа); с ростом беспорядка в системе возрастает энтропия, то есть возрастает наше незнание о системе, другими словами, уменьшаются наши знания о системе.

3. Условная энтропия

Найдем энтропию сложного опыта в том случае, если опыты не являются независимыми, то есть если на исход опыта оказывает влияние результат опыта . Например, пусть в ящике всего два разноцветных шара и опыт состоит в извлечении первого, а опыт – в извлечении второго из них. В этом случае результат опыта полностью снимает неопределенность сложного опыта , то есть оказывается, что , но не . Сумма проявляется лишь для независимых событий!

Связь между зависимыми опытами и состоит в том, что какие-то из исходов могут оказывать влияние на исходы , то есть некоторые пары событий и не являются независимыми. Вернемся к формуле (4.6) для энтропии сложного опыта:

.

В случае зависимых событий: , где – это вероятность наступления исхода опыта при условии, что в опытеимел место исход.

В этом случае по свойству логарифма:

.

После подстановки в формулу (4.6) получаем:

;

;

Устанавливаем порядок суммирования, по аналогии с интегрированием:

В этой формуле:

, так как какое-то из событий обязательно произойдет после того, как произошло событие , поэтому:

;

, в результате

.

,

таким образом,

;

Величины

(4.8)

имеют смысл энтропии опыта при условии, что в опыте реализовался исход . Величину будем называть условной энтропией.

Величина

(4.9)

имеет смысл средней условной энтропии опыта при выполнении опыта . Окончательно получаем для энтропии сложного опыта при условии, что в нем могут быть зависимые исходы:

. (4.10)

Полученное выражение представляет собой общее правило нахождения энтропии сложного опыта. Совершенно очевидно, что выражение (4.5) является частным случаем формулы (4.10) при условии независимости опытов и .

Относительно условной энтропии можно сделать следующие утверждения:

1. Условная энтропия является величиной неотрицательной. 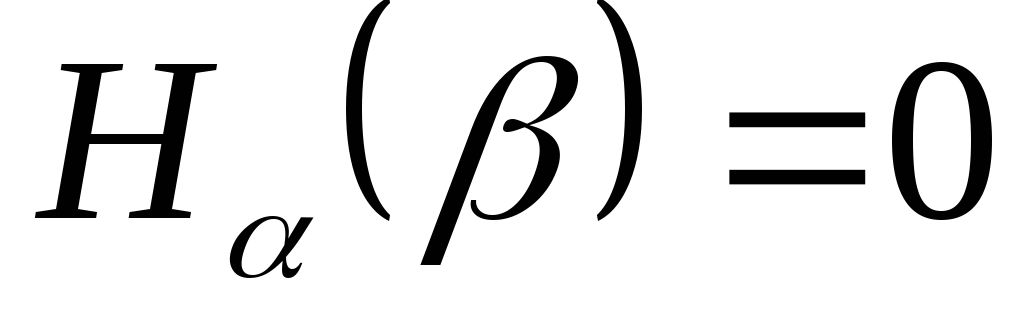только в том случае, если любой исход опыта полностью определяет исход опыта (как в рассмотренном выше примере с двумя разноцветными шарами), то есть при . В этом случае .

2. Если опыты и независимы, то 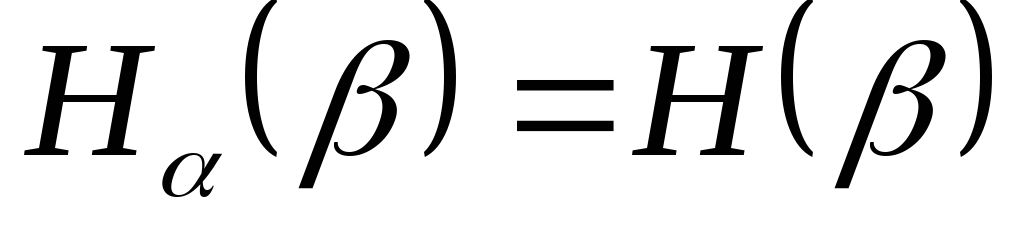, причем

. (4.11)

Другими словами, опыт может либо не оказывать никакого влияния на энтропию опыта(если опыты независимы), либо может понижать энтропию опыта(то есть повысить определенность, повысить наше знание об исходах опыта). Таким образом, условная энтропия не превосходит безусловную.

3. Из соотношений (4.10) и (4.11) следует, что

, (4.12)

причем равенство реализуется только при независимости опытов и.

Пример. В ящике имеются 2 белых и 4 черных шара. Из ящика извлекают последовательно два шара без возврата. Найти энтропию, связанную с первым и вторым извлечениями, а также энтропию обоих извлечений.

Будем считать опытом извлечение первого шара. Он имеет два исхода. Первый исход– вынут белый шар; его вероятность. Второй исход –– вынут черный шар; его вероятность. По формуле (4.4) сразу находим:

.

Опыт – также имеет два исхода.– вынут белый шар,– вынут черный шар, однако вероятности этих исходов зависят от того, каким был исход опыта. Именно,

При :и;

При :и.

Итак, энтропия, связанная со вторым опытом, является условной, и, согласно, формуле (4.8), получаем:

;

.

По формуле (4.9) получаем:

.

По формуле (4.10) получаем:

.

Ответ: ,, .