7. Общая формула для вероятности суммы событий

Обобщим формулу для вероятности наступления суммарного события (3.5) на ситуацию, когда отдельные события имогут оказаться совместными, то есть происходить одновременно. В этом случае получается, что .

Пусть событие выполняется приисходах изравновероятных возможных исходов опыта, а событиевыполняется приисходах из тех жевозможных исходов опыта. Однако из-за того, что возможно совместное выполнение событийи, исходыимогут оказаться не полностью различимыми, то есть среди них могут быть одни и те же исходы. Тогда суммарное количество благоприятных исходов (когда выполняетсяили). Следовательно,

,

то есть получаем .

Определим конкретное значение величины .

Пусть среди исходов иимеютсяобщих исходов, то есть таких, когда событияинаступают одновременно. Вероятностьсовместногособытия (одновременного наступленияи) равна

. (3.15)

Общее количество различныхблагоприятных исходов равно. Тогда вероятность равна

. (3.16)

Таким образом, окончательно получаем:

. (3.17)

В частном случае, когда события инесовместны, , и вместо (3.16) или (3.17) мы получаем формулу (3.5).

Пример. Какова вероятность вынуть из колоды 36 карт козыря или туза, если одна из мастей объявлена козырной? Событие– получение козыря – имеет вероятность, поскольку карт одной масти в колоде имеется 9. Событие– получение туза – имеет вероятность, поскольку тузов 4. Однако один туз является козырным (то есть событияиреализуются одновременно, а такой вариант по условию задачи мынерассматриваем как благоприятное событие); вероятность его появления равна. Тогда, согласно формуле (3.17), получаем:.

С учетом формул (3.14) и (3.16) можно получить самое общее правило сложения вероятностей:

. (3.18)

Лекция 3. Понятие энтропии

1. Энтропия как мера неопределенности

2. Свойства энтропии

3. Условная энтропия

1. Энтропия как мера неопределенности

Случайные события могут быть описаны с использованием понятия «вероятность». Соотношения теории вероятностей позволяют найти (вычислить) вероятности как одиночных случайных событий, так и исходов сложных опытов, объединяющих несколько независимых или связанных между собой событий. Однако описать случайные события можно не только в термнах вероятностей.

То, что событие случайно, означает отсутствие полной уверенности в его наступлении. Это создает неопределенность в исходах опытов, в результате которых данное событие может произойти. Безусловно, степень неопределенности различна для разных ситуаций. Например, если опыт состоит в определении возраста случайно выбранного студента 1-го курса дневного отделения ВУЗа, то с большой степенью уверенности можно лишь утверждать, что он окажется менее 30 лет. При этом с меньшей уверенностью можно утверждать, что возраст произвольно выбранного студента окажется менее 17 лет. Таким образом, существует неопределенность в исходе опыта, который состоит в проверке возраста случайно выбранного студента.

Для практики важно иметь возможность произвести численную оценку неопределенности исходов разных опытов. Попробуем ввести такую количественную меру неопределенности.

Начнем с простой ситуации, когда опыт имеет равновероятных исходов. Очевидно, что неопределенность каждого из них зависит от, то есть мера неопределенности является функцией числа исходов.

Можно сразу указать некоторые свойства этой функции:

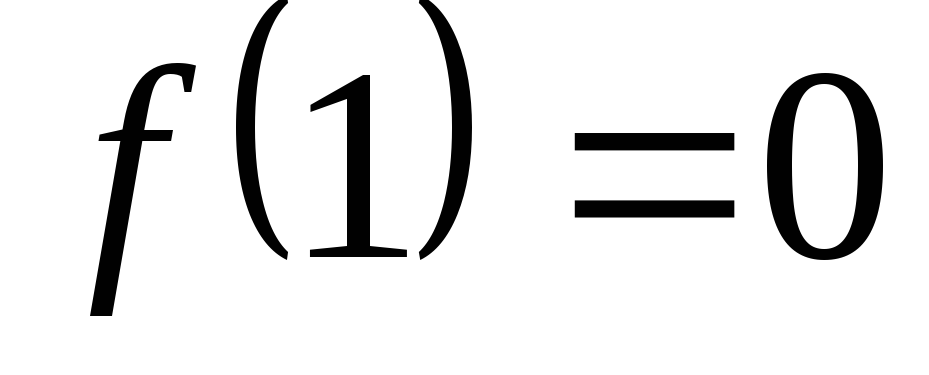• , поскольку при исход опыта не является случайным и, следовательно, неопределенность отсутствует;

• возрастает с ростом , поскольку чем больше число возможных исходов, тем более затруднительным становится предсказание результата опыта.

Попробуем определить явный вид функции . Будем обозначатьопытысо случайными исходами маленькими греческими буквами,и так далее, а отдельныеисходыопытов (события) – латинскими заглавными буквами,и так далее

Рассмотрим два независимыхопытаис количествами равновероятных исходов соответственнои.

Пусть имеет место сложныйопыт, который состоит в одновременном выполнении опытови. Число возможных равновероятных его исходов равно. Очевидно, неопределенность исхода такого сложного опытабудет больше неопределенности опыта, поскольку к ней добавляется неопределенность опыта. Естественно обозначить неопределенность этого сложного опытакак. С другой стороны, меры неопределенности отдельных опытовисоставляют соответственнои. В случае сложного опытапроявляется общая (суммарная) неопределенность совместных событий. Однако из независимостииследует, что в сложном опыте неопределенности каждого изиникак не могут повлиять друг на друга. Следовательно, мера суммарной неопределенности должна быть равна сумме мер неопределенности каждого из опытов, то естьмера неопределенности аддитивна:

. (4.1)

Теперь задумаемся о том, каким может быть явный вид функции , чтобы она удовлетворяла следующим свойствам:

• ;

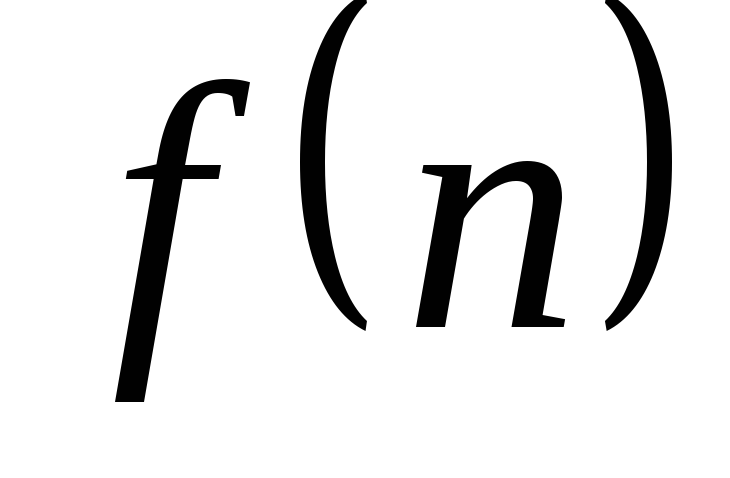• возрастает с ростом ;

• .

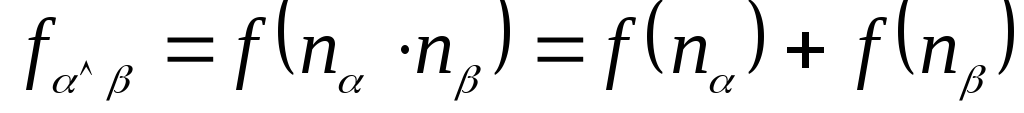Легко увидеть, что такому набору свойств удовлетворяет логарифмическая функция, причем доказано, что онаединственнаяиз всех существующих классов функций.

Таким образом,

За меру неопределенности опыта с равновероятными исходами принимается число.

Отметим, что выбор основания логарифма в данном случае принципиального значения не имеет, так как в силу известной формулы преобразования логарифма от одного основания к другому:

.

Изменение значения основания логарифма связано с выбором единицы измерения неопределенности. Удобным основанием оказывается число 2. В этом случае за единицу измерения неопределенности принимается неопределенность, содержащаяся в опыте, имеющем лишь два равновероятных исхода: , поэтому.

Единица измерения неопределенности называется бит.

1 бит – это неопределенность, заключенная в опыте с двумя равновероятными исходами.

Таким образом, нами установлен явный вид функции, описывающей меру неопределенности исхода опыта, имеющего равновероятных исходов:

. (4.2)

Величина меры неопределенности получила название энтропия. Будем ее обозначатьH.

Вновь рассмотрим опыт с равновероятными исходами. Поскольку каждый исход случаен, он вносит свой вклад в неопределенность всего опыта. Но так как всеисходов равновероятны, разумно допустить, что каждый из этих исходов вносит в опыт одинаковую долю неопределенности. Из свойства аддитивности неопределенности, а также из свойства (4.2) следует, что неопределенность, вносимая одним исходом равна

,

где – вероятность любого из отдельных исходов.

Таким образом, неопределенность, вносимая каждым из равновероятных исходов, равна:

. (4.3)

Теперь обобщим формулу (4.3) на ситуацию, когда исходы опытанеравновероятны и имеют вероятности, где.

Тогда неопределенность, вносимая -м исходом равна

.

По свойству аддитивности неопределенности (энтропии) общая неопределенность опыта равна

. (4.4)

Введенная таким образом величина (4.4), как уже было сказано, называется энтропией опыта .

Энтропия является мерой неопределенности результата опыта, в котором проявляются случайные события, и равна средней неопределенности всех возможных его исходов.

Для практики формула (4.4) важна тем, что позволяет сравнить неопределенности различных опытов со случайными исходами.

Пример 1. Имеются два ящика, в каждом из которых по 12 шаров. В первом – 3 белых, 3 черных и 6 красных; во втором – каждого цвета по 4. Опыты состоят в вытаскивании по одному шару из каждого ящика. Что можно сказать относительно неопределенностей исходов этих опытов? Согласно формуле (4.4) находим энтропии обоих опытов:

;

;

Таким образом, , то есть неопределенность результата в опытевыше, и, следовательно, предсказать его исход можно с меньшей долей уверенности, чем результат опыта.