4. Перевод p  q дробных чисел

Пусть необходимо перевести в Q-ичную систему счисления дробьX, заданную вP-ичной системе счисления. Так как, то числоXвQ-ичной системе можно представить в виде полинома:

, (11.13)

где – искомые коэффициентыQ-ичного разложения числаX.

Определим коэффициент.

Умножим равенство (11.13) по правилам P-ичной арифметики наQ:

. (11.14)

Так как , то в (11.14) можно выделить целую и дробную части:

;

.

Теперь определим коэффициент.

. (11.15)

Умножим обе части (11.15) на Q:

. (11.16)

Теперь в (11.16) выделим целую и дробную части:

;

,

и так далее.

Таким образом, «просматривается» процедура нахождения коэффициентов с помощью следующихрекуррентных формул:

; (11.17)

, (11.18)

где , а также принято.

Процесс нахождения коэффициентов с помощью формул (11.17), (11.18) прожолжается до тех пор, пока не достигается.

Пример. Перевести числов двоичную систему счисления.

Применение формул (11.17), (11.18) приводит к последовательности действий:

, поэтому;

, поэтому;

, поэтому;

, поэтому;

, поэтому;

, поэтому;

, поэтому;

, поэтому;

и так далее, то есть получаем бесконечную периодическую дробь.

Таким образом, в результате перевода точной десятичной дроби получаем бесконечную периодическую двоичную дробь:

, где в скобках указан период полученной дроби.

6. Перевод чисел между 2-ичной, 8-ричной и 16-ричной системами счисления

Интерес к двоичной системе счисления вызван тем, что именно эта система используется для представления чисел в компьютере. Однако двоичная запись оказывается громоздкой по сравнению с другими системами, и, кроме того, она плохо воспринимается и запоминается человеком из-за зрительной однородности (все числа состоят из нулей и единиц). Поэтому в нумерации ячеек памяти компьютера, в записи кодов команд, нумерации регистров и устройств и пр. используются системы счисления с основаниями 8 и 16. Выбор последних обусловлен тем, что переход от них к двоичной системе и обратно осуществляется, как будет показано ниже, весьма простым способом.

Напомним соответствие цифр различных систем счисления (табл. 18).

Табл. 18. Соответствие цифр различных систем счисления

Представление чисел в различных системах счисления
10-ная	2-ичная	8-ричная	16-ричная
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

Для перевода чисел между системами инадо пользоваться следующими правилами:

Правило 1

Для преобразования числа из системыQ в систему (l – целое положительное число) достаточно целую часть данного числа разбить на группы поl цифр справа налево от точки и дробную часть числа разбить на группы поl цифр слева направо от точки, дописывая при необходимости недостающее (до l) количество незначащих нулей в крайней слева и в крайней справа группах цифр. После этого каждую из полученных групп цифр независимо перевести в P-ичную систему счисления.

Пример. Перевести числов 8-ричную систему счисления.

, поэтому. Таким образом,.

Правило 2

Для преобразования числа из системы(l – целое положительное число) в систему Q достаточно каждую цифру числа представить в видеl-разрядного Q-ичного числа, дополняя его при необходимости незначащими нулями слева до группы в l цифр.

Пример. Перевести числов 2-ичную систему счисления.

, поэтому. Таким образом, каждую 16-ричную цифру числанадо представить в виде 4-разрядного 2-ичного числа:.

Переводы , очевидно, удобно осуществлять через промежуточный переход к двоичной системе счисления.

Пример. .

Докажем приведенные выше правила. Очевидно, что оба правила взаимно однозначны, обратимы. Поэтому достаточно доказать правило 2.

Рассмотрим P-ичное число, сокращенная запись которого имеет вид

. (11.19)

Это означает, что

.

(11.20)

Так как , то (11.20) перепишем так:

. (11.21)

Представим в Q-ичной системе каждый из коэффициентов:

, (11.22)

где .

Подставим (11.22) в (11.21):

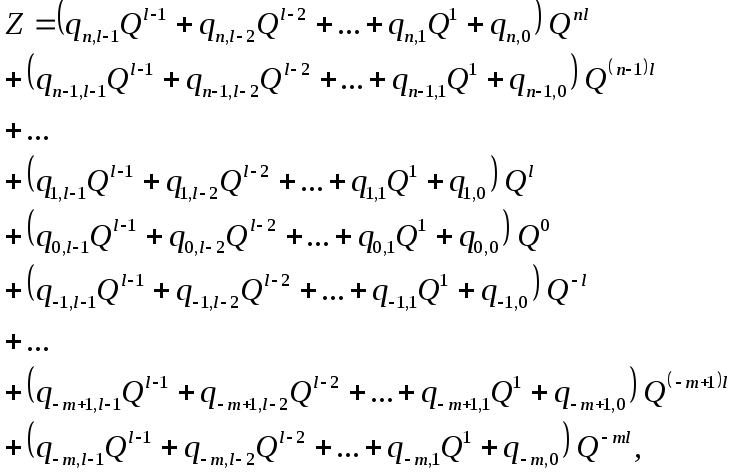(11.23)

или, после элементарных преобразований,

(11.24)

Каждая скобка в (11.23) соответствует P-ичной цифреиз (11.19), причем каждая эта цифрапредставлена вQ-ичной системе в видеQ-ичного числа

,

содержащего lQ-ичных разрядов.

Всего в искомом Q-ичном представлении числаZбудетQ-ичных разрядов (цифр).