
- •Предисловие
- •Лекция 1. Информация. Начальные понятия и определения
- •1. Информация и данные
- •2. Адекватность и формы адекватности информации
- •3. Качество информации
- •4. Понятие об информационном процессе
- •5. Формы представления информации
- •6. Преобразование сообщений
- •Лекция 2. Необходимые сведения из теории вероятностей
- •1. Понятие вероятности
- •2. Сложение вероятностей независимых несовместных событий
- •3. Умножение вероятностей независимых совместных событий
- •4. Нахождение среднего для значений случайных независимых величин
- •5. Понятие условной вероятности
- •6. Общая формула для вероятности произведения событий
- •7. Общая формула для вероятности суммы событий
- •Лекция 3. Понятие энтропии
- •1. Энтропия как мера неопределенности
- •2. Свойства энтропии
- •3. Условная энтропия
- •Лекция 4. Энтропия и информация
- •1. Объемный подход к измерению количества информации
- •2. Энтропийный подход к измерению количества информации
- •Лекция 5. Информация и алфавит
- •Лекция 6. Постановка задачи кодирования. Первая теорема Шеннона.
- •Лекция 7. Способы построения двоичных кодов. Алфавитное неравномерное двоичное кодирование сигналами равной длительности. Префиксные коды.
- •1. Постановка задачи оптимизации неравномерного кодирования
- •00100010000111010101110000110
- •2. Неравномерный код с разделителем
- •3. Коды без разделителя. Условие Фано
- •00100010000111010101110000110
- •00100010000111010101110000110
- •4. Префиксный код Шеннона–Фано
- •5. Префиксный код Хаффмана
- •Лекция 8. Способы построения двоичных кодов. Другие варианты
- •1. Равномерное алфавитное двоичное кодирование. Байтовый код
- •2. Международные системы байтового кодирования текстовых данных. Универсальная система кодирования текстовых данных
- •3. Алфавитное кодирование с неравной длительностью элементарных сигналов. Код Морзе
- •4. Блочное двоичное кодирование
- •101010111001100010000000001000000000000001
- •5. Кодирование графических данных
- •6. Кодирование звуковой информации
- •Лекция 9. Системы счисления. Представление чисел в различных системах счисления. Часть 1
- •1. Системы счисления
- •2. Десятичная система счисления
- •3. Двоичная система счисления
- •4. 8- И 16-ричная системы счисления
- •5. Смешанные системы счисления
- •6. Понятие экономичности системы счисления
- •Лекция 10. Системы счисления. Представление чисел в различных системах счисления. Часть 2.
- •1. Задача перевода числа из одной системы счисления в другую
- •2. Перевод q p целых чисел
- •3. Перевод p q целых чисел
- •4. Перевод p q дробных чисел
- •6. Перевод чисел между 2-ичной, 8-ричной и 16-ричной системами счисления
- •Лекция 11. Кодирование чисел в компьютере и действия над ними
- •1. Нормализованные числа
- •2. Преобразование числа из естественной формы в нормализованную
- •3. Преобразование нормализованных чисел
- •4. Кодирование и обработка целых чисел без знака
- •5. Кодирование и обработка целых чисел со знаком
- •6. Кодирование и обработка вещественных чисел
- •Лекция 12. Передача информации в линии связи
- •1. Общая схема передачи информации в линии связи
- •2. Характеристики канала связи
- •3. Влияние шумов на пропускную способность канала
- •Лекция 13. Обеспечение надежности передачи информации.
- •1. Постановка задачи обеспечения надежности передачи
- •2. Коды, обнаруживающие одиночную ошибку
- •3. Коды, исправляющие одиночную ошибку
- •Лекция 14. Способы передачи информации в компьютерных линиях связи
- •1. Параллельная передача данных
- •2. Последовательная передача данных
- •3. Связь компьютеров по телефонным линиям
- •Лекция 15. Классификация данных. Представление данных в памяти компьютера
- •1. Классификация данных
- •2. Представление элементарных данных в озу
- •Лекция 16. Классификация структур данных
- •1. Классификация и примеры структур данных
- •2. Понятие логической записи
- •Лекция 17. Организация структур данных в оперативной памяти и на внешних носителях
- •1. Организация структур данных в озу
- •2. Иерархия структур данных на внешних носителях
- •3. Особенности устройств хранения информации
- •Контрольные вопросы
- •Список литературы
4. Нахождение среднего для значений случайных независимых величин
Рассмотрим ситуацию, когда случайное
явление – это числовое значение
![]() некоторой величины. Например, число,
указанное на грани игрального кубика;
сумма выигрыша в лотерею и так далее
Пусть этих значений
некоторой величины. Например, число,
указанное на грани игрального кубика;
сумма выигрыша в лотерею и так далее
Пусть этих значений
![]() и они образуют дискретный ряд
и они образуют дискретный ряд
![]() ,
,
![]() ,
…,
,
…,
![]() .
Среди этих значений могут оказаться
одинаковые. Пусть таких групп одинаковых
значений имеется
.
Среди этих значений могут оказаться
одинаковые. Пусть таких групп одинаковых
значений имеется
![]() .
Очевидно, что
.
Очевидно, что
![]() .
Спрашивается, каково среднее значение
величины
.
Спрашивается, каково среднее значение
величины
![]() ?
(Например, сколько в среднем очков
выпадет при одном броске кубика?)
?
(Например, сколько в среднем очков
выпадет при одном броске кубика?)
Будем исходить из определения среднего значения:
![]() . (3.11)
. (3.11)
Однако эта же сумма может быть получена,
если провести суммирование по группам
одинаковых значений. Пусть в каждой
группе одинаковых значений по
![]() .
Тогда:
.
Тогда:
![]() .
.
Так как
![]() – вероятность появления результата из
группы
– вероятность появления результата из
группы![]() ,
то получаем:
,
то получаем:
![]() . (3.12)
. (3.12)
Пример. Найти среднее количество очков, выпадающее при однократном броске игральной кости (кубика).
Так как все
![]() ,
а количество очков
,
а количество очков![]() принимает значения
принимает значения![]() ,
по формуле (3.12) получаем:
,
по формуле (3.12) получаем:
![]() .
.
Величина (3.12) – это взвешенное среднеедля выборки
![]() ,
,
![]() ,
…,
,
…,
![]() .
.
5. Понятие условной вероятности
Отметим, что события
![]() и
и![]() могут бытьзависимыми– это наиболее
общий случай. Зависимость случайных
событий означает, что одно из них
оказывает влияние на другое.
могут бытьзависимыми– это наиболее
общий случай. Зависимость случайных
событий означает, что одно из них
оказывает влияние на другое.
Например, Вы случйно встретили знакомого
на вечеринке (событие
![]() );
однако Ваше появление на этой вечеринке
также событие, строго говоря, случайное
(событие
);
однако Ваше появление на этой вечеринке
также событие, строго говоря, случайное
(событие![]() ).
Таким образом, случайное событие
).
Таким образом, случайное событие![]() оказывается следствием случайного
события
оказывается следствием случайного
события![]() .
.
Заметим, что вероятность любого случайного
события зависит от каких-то условий,
при которых возможно его наступление
или ненаступление. Например, условием
того, что вероятность выпадения всех
цифр игральной кости одинакова и равна
![]() ,
является ее правильная геометрическая
форма и однородность материала. Если
условия изменятся (например, форма будет
не куб, а параллелепипед), то изменится
и вероятность.
,
является ее правильная геометрическая
форма и однородность материала. Если
условия изменятся (например, форма будет
не куб, а параллелепипед), то изменится
и вероятность.
Вероятность события
![]() при условии, что влияющее на него событие
при условии, что влияющее на него событие![]() имело место, называетсяусловной
вероятностью.
имело место, называетсяусловной
вероятностью.
Обозначать условную вероятность будем
![]() .
.
Вероятность событий, для которых условия не изменяются в различных сериях опытов, называется безусловной.
Случайные
события
![]() и
и![]() независимы,
если их условные вероятности равны
безусловным, то есть
независимы,
если их условные вероятности равны
безусловным, то есть
![]() и
и![]() . (3.13)
. (3.13)
Перечислим некоторые свойства условной вероятности:
Если
 и
и несовместны,
то
несовместны,
то
 и
и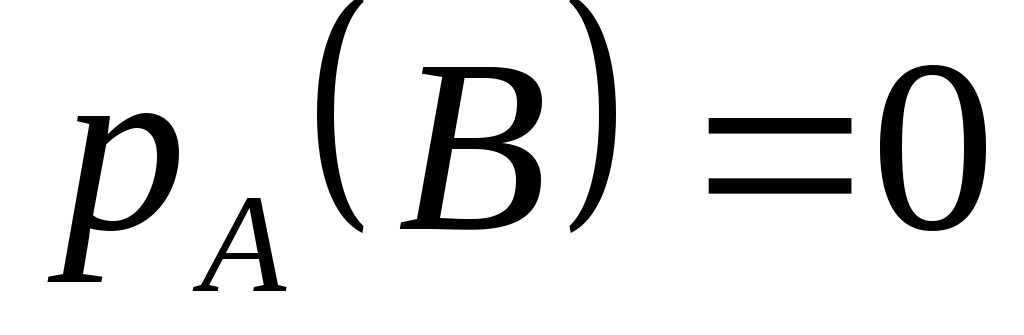 ;
;Для дополнительных событий
 ;
;Если
 и
и
 несовместны, то
несовместны, то
 ,
а также
,
а также
 ;
;Если
 с необходимостью влечет за собой
с необходимостью влечет за собой
 ,
то есть
,
то есть
 ,
то
,
то
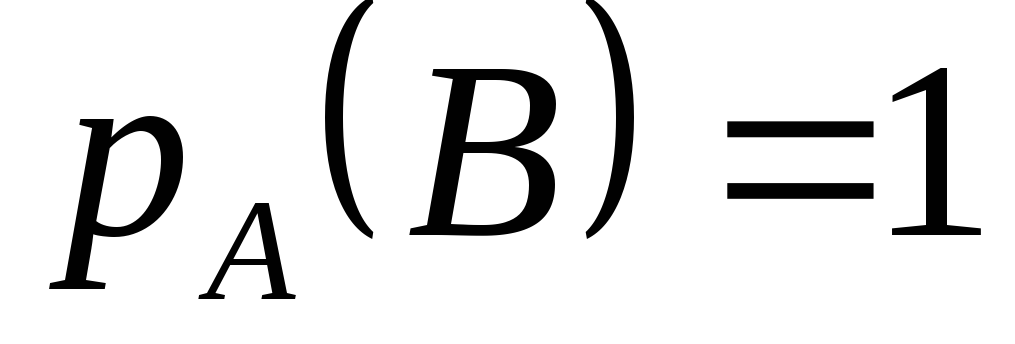 ;
;
6. Общая формула для вероятности произведения событий
Теперь при нахождении вероятности
произведения событий
![]() рассмотрим наиболее общий случай, когда
события
рассмотрим наиболее общий случай, когда
события![]() и
и![]() могут бытьзависимыми.
могут бытьзависимыми.
Пусть
из
![]() равновероятных исходов опыта событие
равновероятных исходов опыта событие
![]() реализуется
реализуется![]() способами. Из этих
способами. Из этих![]() исходов
исходов![]() исходов являются благоприятными для
наступления события
исходов являются благоприятными для
наступления события![]() ,
связанного с событием
,
связанного с событием![]() .
Тогда
.
Тогда![]() .
.
Пример. Имеется 3 урны, содержащие белые и черные шары. В первой урне 2 белых и 4 черных шара, во второй – 3 белых и 3 черных, в третьей – 4 белых и 2 черных. Из одной из урн (неизвестно, из какой) наугад вынут шар. Какова вероятность того, что вынут из первой урны при условии, что шар оказался белым?
Пусть событие
![]() – вытаскивание белого шара, а
– вытаскивание белого шара, а![]() – то, что он вынут из первой урны. Из
всех имеющихся шаров событию
– то, что он вынут из первой урны. Из
всех имеющихся шаров событию![]() благоприятствуют
благоприятствуют![]() шаров; из них лишь
шаров; из них лишь![]() шара благоприятствуют событию
шара благоприятствуют событию![]() .
Таким образом, получаем:
.
Таким образом, получаем:![]() .
.
Вероятность
совместного выполнения событий
![]() и
и![]() равна
равна
![]() .
.
Итак, окончательно получаем:
![]() . (3.14)
. (3.14)
Выражение (3.14) является наиболее общим
правилом умножения вероятностей. В
частном случае независимости событий
![]() и
и![]() из формулы (3.14) при условии (3.13) получаем
формулу (3.9).
из формулы (3.14) при условии (3.13) получаем
формулу (3.9).
Пример. На карточках отдельными буквами написано слово «ПАПАХА». Карточки переворачивают, перемешивают и случайным образом открывают 4 из них. Какова вероятность получить таким путем слово «ПАПА»?
Пусть событие
![]() – извлечение первой «П», событие
– извлечение первой «П», событие![]() – извлечение второй «А»,
– извлечение второй «А»,![]() – третьей «П» и
– третьей «П» и![]() – четвертной «А». Тогда интересующее
нас событие можно записать как
– четвертной «А». Тогда интересующее
нас событие можно записать как![]() .
Его вероятность можно найти, применяя
несколько раз формулу (3.14).
.
Его вероятность можно найти, применяя
несколько раз формулу (3.14).
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Итак, получаем:
![]() .
.
