
- •Предисловие
- •Лекция 1. Информация. Начальные понятия и определения
- •1. Информация и данные
- •2. Адекватность и формы адекватности информации
- •3. Качество информации
- •4. Понятие об информационном процессе
- •5. Формы представления информации
- •6. Преобразование сообщений
- •Лекция 2. Необходимые сведения из теории вероятностей
- •1. Понятие вероятности
- •2. Сложение вероятностей независимых несовместных событий
- •3. Умножение вероятностей независимых совместных событий
- •4. Нахождение среднего для значений случайных независимых величин
- •5. Понятие условной вероятности
- •6. Общая формула для вероятности произведения событий
- •7. Общая формула для вероятности суммы событий
- •Лекция 3. Понятие энтропии
- •1. Энтропия как мера неопределенности
- •2. Свойства энтропии
- •3. Условная энтропия
- •Лекция 4. Энтропия и информация
- •1. Объемный подход к измерению количества информации
- •2. Энтропийный подход к измерению количества информации
- •Лекция 5. Информация и алфавит
- •Лекция 6. Постановка задачи кодирования. Первая теорема Шеннона.
- •Лекция 7. Способы построения двоичных кодов. Алфавитное неравномерное двоичное кодирование сигналами равной длительности. Префиксные коды.
- •1. Постановка задачи оптимизации неравномерного кодирования
- •00100010000111010101110000110
- •2. Неравномерный код с разделителем
- •3. Коды без разделителя. Условие Фано
- •00100010000111010101110000110
- •00100010000111010101110000110
- •4. Префиксный код Шеннона–Фано
- •5. Префиксный код Хаффмана
- •Лекция 8. Способы построения двоичных кодов. Другие варианты
- •1. Равномерное алфавитное двоичное кодирование. Байтовый код
- •2. Международные системы байтового кодирования текстовых данных. Универсальная система кодирования текстовых данных
- •3. Алфавитное кодирование с неравной длительностью элементарных сигналов. Код Морзе
- •4. Блочное двоичное кодирование
- •101010111001100010000000001000000000000001
- •5. Кодирование графических данных
- •6. Кодирование звуковой информации
- •Лекция 9. Системы счисления. Представление чисел в различных системах счисления. Часть 1
- •1. Системы счисления
- •2. Десятичная система счисления
- •3. Двоичная система счисления
- •4. 8- И 16-ричная системы счисления
- •5. Смешанные системы счисления
- •6. Понятие экономичности системы счисления
- •Лекция 10. Системы счисления. Представление чисел в различных системах счисления. Часть 2.
- •1. Задача перевода числа из одной системы счисления в другую
- •2. Перевод q p целых чисел
- •3. Перевод p q целых чисел
- •4. Перевод p q дробных чисел
- •6. Перевод чисел между 2-ичной, 8-ричной и 16-ричной системами счисления
- •Лекция 11. Кодирование чисел в компьютере и действия над ними
- •1. Нормализованные числа
- •2. Преобразование числа из естественной формы в нормализованную
- •3. Преобразование нормализованных чисел
- •4. Кодирование и обработка целых чисел без знака
- •5. Кодирование и обработка целых чисел со знаком
- •6. Кодирование и обработка вещественных чисел
- •Лекция 12. Передача информации в линии связи
- •1. Общая схема передачи информации в линии связи
- •2. Характеристики канала связи
- •3. Влияние шумов на пропускную способность канала
- •Лекция 13. Обеспечение надежности передачи информации.
- •1. Постановка задачи обеспечения надежности передачи
- •2. Коды, обнаруживающие одиночную ошибку
- •3. Коды, исправляющие одиночную ошибку
- •Лекция 14. Способы передачи информации в компьютерных линиях связи
- •1. Параллельная передача данных
- •2. Последовательная передача данных
- •3. Связь компьютеров по телефонным линиям
- •Лекция 15. Классификация данных. Представление данных в памяти компьютера
- •1. Классификация данных
- •2. Представление элементарных данных в озу
- •Лекция 16. Классификация структур данных
- •1. Классификация и примеры структур данных
- •2. Понятие логической записи
- •Лекция 17. Организация структур данных в оперативной памяти и на внешних носителях
- •1. Организация структур данных в озу
- •2. Иерархия структур данных на внешних носителях
- •3. Особенности устройств хранения информации
- •Контрольные вопросы
- •Список литературы
Лекция 4. Энтропия и информация
Объемный подход к измерению количества информации
Энтропийный подход к измерению количества информации
1. Объемный подход к измерению количества информации
Объем
данных
![]() в сообщении измеряется количеством
символов (разрядов) в этом сообщении. В
различных системах счисления один
разряд имеет различный вес. Также в
различных системах счисления различны
единицы измерения объема данных.
в сообщении измеряется количеством
символов (разрядов) в этом сообщении. В
различных системах счисления один
разряд имеет различный вес. Также в
различных системах счисления различны
единицы измерения объема данных.
В двоичной системе счисления единица измерения количества информации – бит (bit – binary digit – двоичная цифра, двоичный разряд). В десятичной системе счисления единица измерения – дит (десятичный разряд).
Создатели компьютеров отдают предпочтение именно двоичной системе счисления потому, что в техническом устройстве наиболее просто реализовать два противоположных физических состояния. Имеется в виду некоторый физический элемент, имеющий два различных состояния: намагниченность в двух противоположных направлениях; прибор, пропускающий или не пропускающий электрический ток; конденсатор, заряженный или незаряженный; и т.п.
В компьютере бит является наименьшей возможной единицей информации. Объем данных, записанных двоичными знаками в памяти компьютера или на внешнем носителе информации, подсчитывается просто по количеству требуемых для такой записи двоичных символов. При этом, естественно, невозможно нецелое число битов.
Для удобства использования введены и более крупные, чем бит, единицы количества информации:
8 бит = 1 байт;
1024 байта = 1 килобайт (Кбайт);
1024 килобайта = 1 мегабайт (Мбайт);
1024 магабайта = 1 гигабайт (Гбайт);
Кроме объемного подхода к измерению количества информации (в этом случае уместно говорить о количестве данных) существует вероятностный подход к измерению количества информации.
2. Энтропийный подход к измерению количества информации
Как выяснено в предыдущей лекции,
предшествующий опыт
![]() может уменьшить количество исходов
последующего опыта
может уменьшить количество исходов
последующего опыта![]() и, следовательно, уменьшить его
неопределенность.Разностьвеличин
и, следовательно, уменьшить его
неопределенность.Разностьвеличин![]() и
и![]() ,
очевидно, показывает, какие новые
сведения относительно опыта
,
очевидно, показывает, какие новые
сведения относительно опыта![]() мы получаем, произведя опыт
мы получаем, произведя опыт![]() .
Эта величина называетсяинформацией
относительно опыта
.
Эта величина называетсяинформацией
относительно опыта
![]() ,
содержащейся в опыте
,
содержащейся в опыте![]() :
:
![]() . (5.1)
. (5.1)
Данное выражение открывает возможность численного измерения количества информации, поскольку оценивать энтропию мы уже умеем. Из формулы (5.1) легко получить ряд следствий:
Следствие 1. Поскольку единицей измерения энтропии является бит, то в этих же единицах может быть измерено количество информации.
Следствие 2. Пусть опыт![]() ,
то есть просто произведен опыт
,
то есть просто произведен опыт![]() сам по себе. Поскольку результат его
несет полную информацию о себе самом,
неопределенность исхода этого опыта
полностью снимается, то есть
сам по себе. Поскольку результат его
несет полную информацию о себе самом,
неопределенность исхода этого опыта
полностью снимается, то есть![]() .
Тогда из (5.1) следует:
.
Тогда из (5.1) следует:![]() .
.
Тогда можно считать, что энтропия опыта равна той информации, которую мы получаем в результате его осуществления.
Отметим ряд свойств информации:
 ,
причем
,
причем тогда и только тогда, когда опыты
тогда и только тогда, когда опыты и
и независимы. При этом опыты не несут
никакой информации друг относительно
друга.
независимы. При этом опыты не несут
никакой информации друг относительно
друга.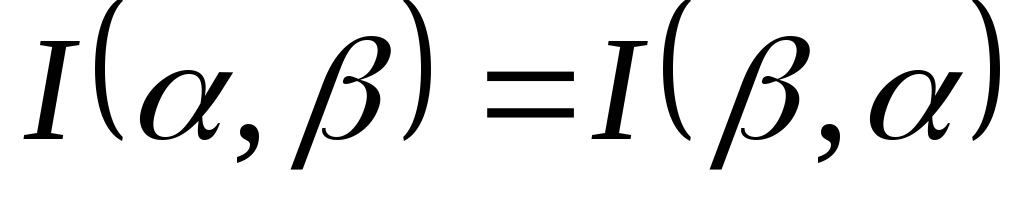 ,
то есть информация симметрична
относительно последовательности
опытов.
,
то есть информация симметрична
относительно последовательности
опытов.Из Следствия 2, которое гласит
 ,
а также из представления энтропии в
виде
,
а также из представления энтропии в
виде (формула (4.4) из предыдущей лекции)
следует, что
(формула (4.4) из предыдущей лекции)
следует, что
![]() . (5.2)
. (5.2)
Таким образом, информация опыта равна среднему значению неопределенности, содержащейся в каком-либо одном его исходе).
Пример. Какое количество информации требуется, чтобы узнать исход броска монеты?
По формуле (5.2):
![]() ;
;
![]() – вероятность выпадения герба;
– вероятность выпадения герба;
![]() – вероятность выпадения решки;
– вероятность выпадения решки;
![]() .
.
Пример. Игра. Некто задумал целое число в интервале от 0 до 3. Наш опыт состоит в угадывании этого числа. На наши вопросы Некто может отвечать лишь «Да» или «Нет» (то есть давать бинарные ответы). Какое количество информации должны мы получить, чтобы узнать задуманное число, то есть полностью снять начальную неопределенность? Как правильно построить процесс угадывания?
Исходами (их всего 4) в данном случае
являются:
![]() – задуман 0;
– задуман 0;![]() – задумана 1;
– задумана 1;![]() – задумана 2;
– задумана 2;![]() – задумана 3. Конечно, предполагается,
что вероятности быть задуманными у всех
чисел одинаковы, поэтому
– задумана 3. Конечно, предполагается,
что вероятности быть задуманными у всех
чисел одинаковы, поэтому![]() ,
где
,
где![]() .
.
![]() .
.
По формуле (5.2):
![]() .
.
Таким образом, для полного снятия неопределенности опыта (для угадывания задуманного числа) нам необходимо 2 бит информации.
Выясним, какие вопросы необходимо задать, чтобы процесс угадывания был оптимальным, то есть содержал минимальное число вопросов. Здесь удобно воспользоваться так называемым выборочным каскадом (рис. 1):

Рис. 1. Выборочный каскад
Таким образом, для решения этой задачи оказалось достаточно двух вопросов. Совпадение между количеством информации и числом вопросов с бинарными ответами неслучайно.
Количество информации численно равно количеству вопросов с равновероятными бинарными вариантами ответов, которые необходимо задать, чтобы полностью снять неопределенность задачи.
В рассмотренном примере два полученных ответа в выборочном каскаде полностью сняли начальную неопределенность. Подобная процедура позволяет определить количество информации в любой задаче, интерпретация которой может быть сведена к парному выбору. Данное утверждение перестает быть справедливым в том случае, если каждый из двух возможных ответов имеет разную вероятность – такая ситуация будет рассмотрена позднее.
Получим следствие формулы (5.2) для случая,
когда все
![]() исходов опыта
исходов опыта
![]() равновероятны. Именно такие опыты и
рассматривались в примерах 1 и 2. В этом
случае все
равновероятны. Именно такие опыты и
рассматривались в примерах 1 и 2. В этом
случае все
![]() ,
,
и, следовательно, формулу (5.2) можно переписать так:
![]() .
.
Таким образом,
![]() . (5.3)
. (5.3)
Эта формула была выведена в 1928 году
инженером Р.Хартли (США) и носит
его имя. Онасвязывает количество
равновероятных состояний
![]() и количество информации
и количество информации![]() в сообщении о том, что какое-то из этих
состояний реализовалось.
в сообщении о том, что какое-то из этих
состояний реализовалось.
Смысл формулы: если некоторое множество
сожержит
![]() элементов и
элементов и![]() принадлежит этому множеству, то для его
выделения (однозначной идентификации)
среди прочих требуется количество
информации, равное
принадлежит этому множеству, то для его
выделения (однозначной идентификации)
среди прочих требуется количество
информации, равное![]() (см. приведенные выше примеры с броском
монеты и с угадыванием задуманного
числа из некоторого интервала).
(см. приведенные выше примеры с броском
монеты и с угадыванием задуманного
числа из некоторого интервала).
Частным случаем применения формулы
(5.3) является ситуация, когда число
![]() возможных состояний (исходов опыта)
можно представить в виде
возможных состояний (исходов опыта)
можно представить в виде![]() .
Именно эта ситуация реализовалась в
рассмотренных выше двух примерах.
Подставляя
.
Именно эта ситуация реализовалась в
рассмотренных выше двух примерах.
Подставляя![]() в формулу (5.3), получаем:
в формулу (5.3), получаем:
![]() . (5.4)
. (5.4)
Анализируя результаты решения задач в
примерах, можно прийти к выводу, что
число
![]() как раз равно количеству вопросов с
бинарными равновероятными ответами.
Число этих вопросов и определяет
количество информации об опыте (о
результате (исходе) опыта).
как раз равно количеству вопросов с
бинарными равновероятными ответами.
Число этих вопросов и определяет
количество информации об опыте (о
результате (исходе) опыта).
Пример. Случайным образом вынимается карта из колоды в 32 карты. Какое количество информации требуется, чтобы угадать, что это за карта?
Для данной ситуации возможных исходов
![]() .
Значит,
.
Значит,![]() ,
следовательно,
,
следовательно,![]() .
.
Попытаемся понять смысл полученных в данном разделе результатов. Необходимо выделить ряд моментов.
Выражение (5.2) является статистическимопределением понятия «информация», поскольку в него входят вероятности возможных исходов опыта. По сути, формулой (5.2) даетсяоперационноеопределение величины информации, то есть устанавливаетсяпроцедура(способ)измерениявеличины. В науке именно такой метод введения новых понятий (величин) считается предпочтительным, поскольку то, что не может быть измерено, не может быть проверено, и, следовательно, заслуживает меньшего доверия (или не заслуживает доверия вовсе).
Выражение (5.1) можно интерпретировать следующим образом. Если начальная энтропия опыта равна
 ,
а в результате сообщения информации
,
а в результате сообщения информации энтропия становится равной
энтропия становится равной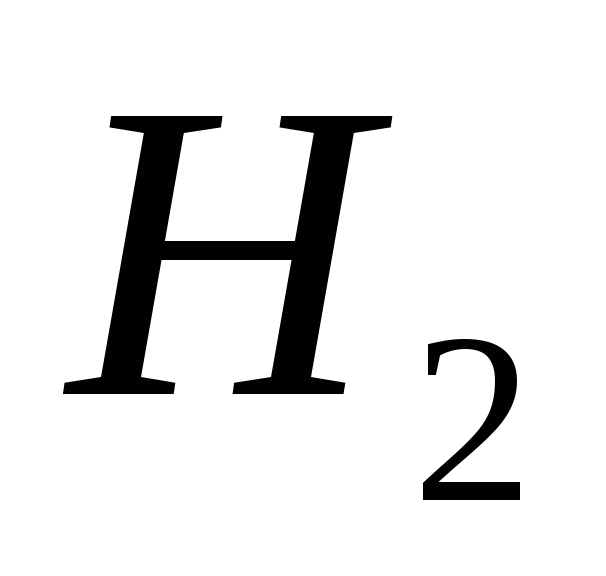 (очевидно, что
(очевидно, что ),
то ясно, что формулу (5.1) можно переписать
так:
),
то ясно, что формулу (5.1) можно переписать
так:
![]() ,
,
то есть информация равна убыли энтропии.
В частном случае, если изначально
равновероятных исходов в опыте было
![]() ,
а в результате передачи информации
,
а в результате передачи информации![]() неопределенность в исходе (результате)
опыта уменьшилась, и число исходов стало
неопределенность в исходе (результате)
опыта уменьшилась, и число исходов стало![]() (очевидно, что
(очевидно, что![]() ),
то из (5.1) получается:
),
то из (5.1) получается:
![]() .
.
Таким образом, можно дать следующее определение понятия информации:
Информация – это содержание сообщения, понижающего неопределенность некоторого опыта с неоднозначным исходом; убыль связанной с этим опытом энтропии является количественной мерой информации.
В случае равновероятных исходов некоторого опыта информация равна логарифму (по основанию 2) отношения числа возможных исходов этого опыта до и после получения информации.
Как уже ранее было сказано, в статистической механике энтропия характеризует неопределенность, связанную с недостатком информации о состоянии системы. Наибольшей оказывается энтропия у равновесной полностью беспорядочной системы – о ее состоянии наша осведомленность минимальна. Упорядочение системы (наведение какого-то порядка) связано с получением некоторой дополнительной информации и уменьшением энтропии.
В теории информации энтропия также отражает неопределенность, однако, это неопределенность иного рода – она связана с незнанием результата опыта с набором случайных возможных исходов.
Таким образом, между энтропией в физике и информатике много общего. Однако необходимо осознавать и различие. Совершенно очевидно, что в дальнейшем в данном курсе мы будем использовать понятие энтропии в аспекте теории информации.
Следствием аддитивности энтропии независимых опытов (см. формулу (4.5) из предыдущей лекции) является аддитивность информации.
Докажем это.
Пусть с выбором одного из элементов
![]() множества
множества![]() ,
содержащего
,
содержащего![]() элементов, связано
элементов, связано![]() информации, а с выбором одного из
элементов
информации, а с выбором одного из
элементов![]() множества
множества![]() ,
содержащего
,
содержащего![]() элементов, связано
элементов, связано![]() информации. Пусть второй выбор никак
не связан с первым, тогда при объединении
множеств число возможных состояний
(вариантов общего выбора) будет
информации. Пусть второй выбор никак
не связан с первым, тогда при объединении
множеств число возможных состояний
(вариантов общего выбора) будет![]() .
Тогда для определения (отбора) определенной
(конкретной) комбинации элементов
.
Тогда для определения (отбора) определенной
(конкретной) комбинации элементов![]() потребуется количество информации:
потребуется количество информации:
![]() ,
,
что и требовалось доказать.
Вернемся к утверждению о том, что количество информации (в битах) численно равно количеству вопросов с двумя равновероятными вариантами ответа. Означает ли это, что информация
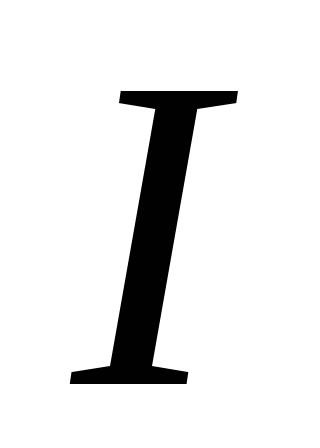 должна быть всегда величиной целой? Из
формулы Хартли (5.3) следует, что
должна быть всегда величиной целой? Из
формулы Хартли (5.3) следует, что (
( – целое число бит) только в случае
– целое число бит) только в случае .
А в остальных ситуациях? Например, если
нужно угадать число от 0 до 6 (всего 7
равновероятных исходов), необходимо
получить
.
А в остальных ситуациях? Например, если
нужно угадать число от 0 до 6 (всего 7
равновероятных исходов), необходимо
получить информации. Поэтому для угадывания
числа от 0 до 7 нужно задать 3 (три) вопроса,
поскольку число вопросов, естественно,
может быть только целым.
информации. Поэтому для угадывания
числа от 0 до 7 нужно задать 3 (три) вопроса,
поскольку число вопросов, естественно,
может быть только целым.
Однако представим, что мы одновременно угадываем шесть целых чисел, каждое из которых находится в интервале от 0 до 6 включительно. Таким образом, необходимо отгадать одну из возможных комбинаций, которых в этой ситуации всего
![]() ,
где
,
где![]() .
.
Но полученное число комбинаций
![]() меньше, чем
меньше, чем![]() (хотя и больше, чем
(хотя и больше, чем![]() ).
Следовательно, для угадывания всей
шестизначной комбинации требуется
).
Следовательно, для угадывания всей
шестизначной комбинации требуется![]() информации, то есть нужно задать 17
вопросов. В среднем на угадывание одного
из элементов (чисел), входящих в эту
шестизначную комбинацию, приходится
информации, то есть нужно задать 17
вопросов. В среднем на угадывание одного
из элементов (чисел), входящих в эту
шестизначную комбинацию, приходится![]() вопроса, что близко к значению
вопроса, что близко к значению![]() .
.
Таким образом, величина
![]() ,
определяемая описанным выше способом,
показывает, сколько в среднем необходимо
сделать парных выборов (задать вопросов
с равновероятными бинарными ответами)
для установления результата опыта
(полного снятия неопределенности), когда
число возможных исходов велико (
,
определяемая описанным выше способом,
показывает, сколько в среднем необходимо
сделать парных выборов (задать вопросов
с равновероятными бинарными ответами)
для установления результата опыта
(полного снятия неопределенности), когда
число возможных исходов велико (![]() ).
).
Необходимо понимать также, что не всегда с каждым из ответов на вопрос, имеющий только два варианта ответа (мы называем такие вопросы бинарными), связан ровно 1 бит информации.
Рассмотрим опыт, реализующийся посредством
двух случайных событий. Поскольку их
(этих случайных событий) всего два,
очевидно, что они являются дополнительнымидруг другу. Если эти события равновероятны,
то их вероятности![]() ,
поэтому информация, связанная с опытом,
в результате которого появляется одно
из этих событий, равна
,
поэтому информация, связанная с опытом,
в результате которого появляется одно
из этих событий, равна![]() ,
как следует из (5.2) и из формулы Хартли.
Однако, если вероятности этих событий
различны (
,
как следует из (5.2) и из формулы Хартли.
Однако, если вероятности этих событий
различны (![]() ,
,![]() ),
то из формулы (5.2) получаем функцию:
),
то из формулы (5.2) получаем функцию:
![]() .
.
На рис. 2представлен
график функции![]() .
.
Видно, что при
![]() и при
и при![]() функция
функция![]() .
В частности, кривая
.
В частности, кривая![]() симметрична относительно прямой
симметрична относительно прямой![]() и достигает максимума
и достигает максимума![]() .
.
|
|
Рис. 2. График функции I(p).
Если теперь считать, что событие «1» – это утвердительный ответ на бинарный вопрос, а событие «2» – это отрицательный ответ на этот бинарный вопрос, то приходим к следующему заключению:
Ответ на бинарный вопрос может содержать не более 1 бит информации. При этом информация равна 1 бит только в случае равновероятных бинарных ответов; в остальных случаях информация меньше 1 бит.
Пример. При угадывании результата броска игральной кости задается вопрос: «Выпало 6?» Какое количество информации содержит ответ?
Утвердительный ответ имеет вероятность
![]() .
.
Отрицательный ответ имеет вероятность
![]() .
.
Таким образом, по формуле (5.2):
![]() ;
;
![]() ;
;
![]() .
.
Формула (5.2) приводит еще к одному выводу. Предположим, что некоторый опыт имеет два исхода:
 и
и ,
причем пусть
,
причем пусть ,
а
,
а .
С исходом
.
С исходом связана неопределенность
связана неопределенность ,
поэтому, чтобы снять такую неопределенность,
то есть узнать, что произойдет именно
это событие, надо получить информацию
,
поэтому, чтобы снять такую неопределенность,
то есть узнать, что произойдет именно
это событие, надо получить информацию .
С исходом
.
С исходом связана неопределенность
связана неопределенность ,
поэтому, чтобы снять такую неопределенность,
надо получить информацию
,
поэтому, чтобы снять такую неопределенность,
надо получить информацию .
.
Таким образом, больше неопределенности(необходимой для ее снятия информации)
связано с теми событиями (исходами
опыта), которые менее вероятны.
Действительно, то, что произойдет именно![]() ,
мы почти наверняка знали и до опыта;
поэтому реализация этого исхода добавляет
мало к нашей осведомленности о результате
опыта. Наоборот, исход
,
мы почти наверняка знали и до опыта;
поэтому реализация этого исхода добавляет
мало к нашей осведомленности о результате
опыта. Наоборот, исход![]() – весьма редкий (трудноожидаемый);
неопределенности с ним связано больше,
поэтому и информации надо получить
больше, чтобы узнать, что произойдет
именно событие
– весьма редкий (трудноожидаемый);
неопределенности с ним связано больше,
поэтому и информации надо получить
больше, чтобы узнать, что произойдет
именно событие![]() .
Однако при многократных повторах опыта
такое количество информации мы получать
не будем, так как событие
.
Однако при многократных повторах опыта
такое количество информации мы получать
не будем, так как событие![]() маловероятно и будет происходить редко.
Среднее же количество информации на
один исход, то есть информация об опыте,
согласно формуле (5.2) равна
маловероятно и будет происходить редко.
Среднее же количество информации на
один исход, то есть информация об опыте,
согласно формуле (5.2) равна![]() .
.
Обратим внимание на соотношение понятий «информация» и «знание». На бытовом уровне, а также в науках социальной направленности, понятие «информация» отождествляется с «информированностью», то есть человеческим знанием, которое связано с оценкой смысла информации. В теории информации же, напротив, информация является мерой нашего незнания (неопределенности)чего-либо (например, исхода опыта, который (исход) в принципе может произойти с какой-либо вероятностью); как только опыт произведен и мы узнаем результат опыта, неопределенность, связанная с уже произошедшим исходом, исчезает. Нам не нужна информация о том, что мы знаем, то есть, говоря формально, нам нужна нулевая информация о том, что мы знаем. Другими словаим, состоявшееся событие не несет информации, поскольку пропадает связанная с ним неопределенность, и поэтому в такой ситуации
 .
.

