1.1.2. Операции над множествами

Два множества А и В равны (А = В), если они состоят из одних и тех же элементов.

Например, если A = {1, 2, 3, 4}, B = {3, 1, 4, 2}, то А = В.

Объединением (суммой) множеств А и В называется множество А  В, элементы которого принадлежат хотя бы одному из этих множеств.

Например, если A = {1, 2, 4}, B = {3, 4, 5, 6}, то А  В = {1, 2, 3, 4, 5, 6}.

Если объединяются n множеств, то записывают .

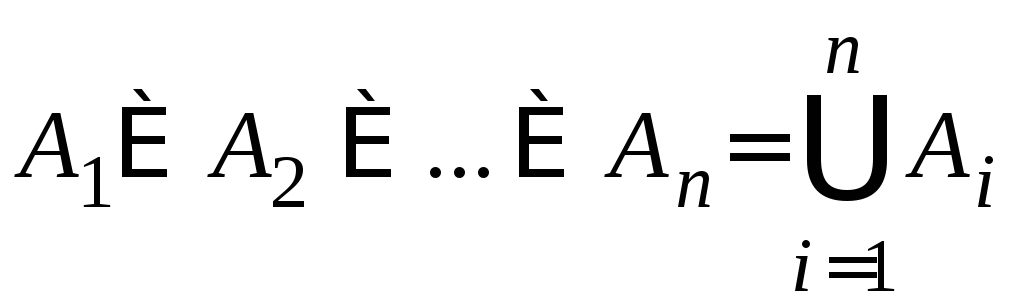Пересечением (произведением) множеств А и В называется множество А  В, элементы которого принадлежат как множеству А, так и множеству В.

Например, если A = {1, 2, 4}, B = {3, 4, 5, 2}, то А  В = {2, 4}.

Если множество является пересечением n множеств, то записывают .

Разностью множеств А и В называется множество А \ В, элементы которого принадлежат множеству А, но не принадлежат множеству В.

Например, если A = {1, 2, 3, 4}, B = {3, 4, 5}, то А \ В = {1, 2}.

Симметрической разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств А \ В и В \А , т. е.

А Δ В = (А \ В)  (В \А).

Например, если A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, то А Δ В = {1, 2}{5, 6}= = {1, 2, 5, 6}.

1.1.3. Свойства операций над множествами

1. Свойство перестановочности (коммутативность) для объединения и пересечения множеств, т. е. А  В = В  А; А  В = В  А.

2. Сочетательное свойство (ассоциативность) для объединения и пересечения множеств, т. е. (А  В)  С= А  (В  С); (А  В)  С= А (ВС).

3. Распределительное свойство (дистрибутивность) для объединения и пересечения множеств:

1) (А  В)  С= (А  С)  (В  С);

2) А  (В  С) = (А  В)  (А  С);

3) (А  В)  С= (А  С)  (В  С);

4) А  (В  С) = (А  В)  (А  С).

Разность множеств не обладает этими свойствами.

Если множество В содержится в множестве D (В  D), то разность D \ В

называется дополнением множества В до множества D. Записывают . Для дополнений множеств справедливзакон Моргана:

1) ; 2).

1.1.4. Декартово произведение множеств

Декартовым произведением множеств называется множество точек. В частном случае, если,, то.

1.1.5. Модуль числа, его свойства

По определению

1) ;

2) ;

3) или;

4) .

1.1.6. Грани числовых множеств

Число К называется верхней гранью множества А, если .

Если С > 0, то К + С также является верхней гранью этого множества.

Число k называется нижней гранью множества А, если . ЕслиС > 0, то k  С также является нижней гранью этого множества.

Аксиома отделимости. Если и, то существует такое числос, что и.

Среди множества верхних граней K + С множества А существует наименьшая верхняя грань M, которая называется точной верхней гранью или «супремум» М = sup (A). Также среди множества нижних граней k  С для множества А существует наибольшая нижняя грань m, которая называется точной нижней гранью или «инфимум» m = inf (A).

Например: 1) если А = [0; 1], то sup (A) = 1, inf (A) = 0; 2) если А = (0; 1), то sup (A) = 1, inf (A) = 0.

1.1.7. Счетные и несчетные множества

Для того, чтобы сравнить два каких-либо множества А и В, между их элементами устанавливают соответствие.

Если это соответствие взаимнооднозначное, то множества называются эквивалентными или равномощными, А  В или А  В.

Примеры:

1. Множества А = {1, 2, 3, …, n, …} и являются равномощными, т. к. между их элементами можно установить взаимнооднозначное соответствие: 1 , 2 , 3 , …,n  , ….

2. Множество точек катета BC и гипотенузы AC треугольника ABC являются равномощными (рис. 1).

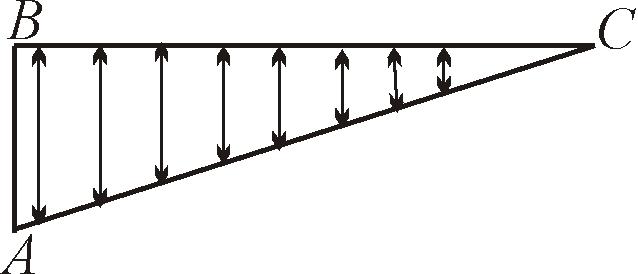
Рис. 1

3. Можно установить взаимнооднозначное соответствие между точками отрезка [0; 1] и множеством точек всей числовой прямой (∞; +∞). Построим полуокружность радиуса r = 0,5 с центром в точке С (0,5; 0,5) (рис. 2).

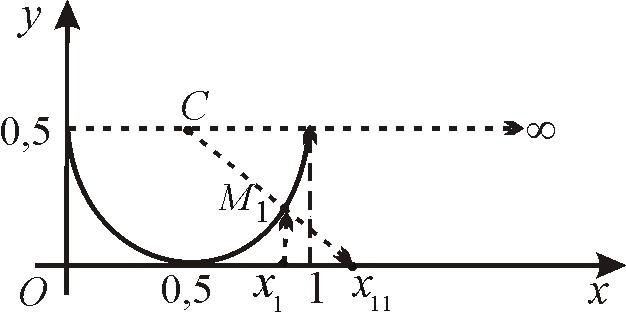
Рис. 2

Через точку , принадлежащую отрезку [0; 1], проведем прямую параллельно осиOy до пересечения с полуокружностью в точке . Через точкиС и проведем прямую до пересечения с осьюOx в точке . Следовательно, точкесоответствует точкаи наоборот. Таким образом, можно установить соответствие между любой точкой отрезка [0; 1] и точкой множества точек числовой прямой (∞; +∞). В частности, если = 0,5, то= 0,5; если= 1, то=. Следовательно, эти множества равномощные, [0; 1]  (∞; ∞).

Последовательностью называется множество чисел, перенумерованных с помощью натуральных чисел и расставленных в порядке возрастания их номеров .

Счетным множеством называется множество эквивалентное множеству натуральных чисел.

Следовательно, любая последовательность является счетным множеством.

Предложение 1. Для того, чтобы множество было счетным, необходимо и достаточно, чтобы его можно было представить в виде последовательности.

Предложение 2. Декартово произведение конечного или счетного числа счетных множеств является счетным множеством.

Предложение 3. Любое подмножество счетного множества является либо конечным, либо счетным.

Таким образом, счетное множество является наименее мощным из бесконечных множеств.

Более мощным, чем счетное множество, является множество действительных чисел . Его мощность называют мощностьюконтинуума. Так как [0; 1]  R, то множество точек отрезка [0; 1] обладает также мощностью континуума.