
- •В. Г. Шершнев математический анализ
- •Часть I. Дифференциальное исчисление
- •Оглавление
- •Календарно-тематический план Распределение часов по темам и видам работ
- •Глава I. Введение в математический анализ
- •1.1. Множества
- •1.1.1. Определение множества
- •1.1.2. Операции над множествами
- •1.1.3. Свойства операций над множествами
- •1.1.4. Декартово произведение множеств
- •1.1.5. Модуль числа, его свойства
- •1.1.6. Грани числовых множеств
- •1.1.7. Счетные и несчетные множества
- •1.2. Функции, их классификация
- •1.3. Предел последовательности
- •1.4. Предел функции
- •1.4.1. Определение предела функции
- •1.4.2. Геометрический смысл предела
- •1.4.3. Односторонние пределы. Необходимое и достаточное условия существования предела функции
- •1.5. Бесконечно малые и бесконечно большие функции
- •1.5.1. Определение бесконечно малой и бесконечно большой функций
- •1.5.2. Свойства бесконечно малых функций
- •1.6. Теоремы о представлении функции в виде суммы предела и бесконечно малой функции
- •1.7. Теоремы о пределах (свойства пределов)
- •1.8. Замечательные пределы
- •1.8.1. Первый замечательный предел
- •1.8.2. Второй замечательный предел
- •1.8.3. Применение второго замечательного предела в финансовых вычислениях
- •1.9. Сравнение бесконечно малых функций
- •1.10. Непрерывность функции в точке и на отрезке
- •1.10.1. Определение непрерывности функции
- •1.10.2. Действия над непрерывными функциями
- •1.10.3. Непрерывность элементарных функций
- •1.10.4. Свойства непрерывных функций
- •1.10.5. Точки разрыва функций
1.6. Теоремы о представлении функции в виде суммы предела и бесконечно малой функции
Теорема
1.3. Если
функция имеет предел
![]() ,
то ее можно представить в виде суммы
предела и бесконечно малой функции,
т.е.
,
то ее можно представить в виде суммы
предела и бесконечно малой функции,
т.е.![]() ,
где
,
где![]() при
при![]() .
.
Д
о к а з а т е л ь с т в о. По определению
предела
![]()
![]()
![]() .
Отсюда следует, что
.
Отсюда следует, что
![]() при
при![]() ,
т. е.
,
т. е.![]() .
.
Теорема
1.4. Если
функция
![]() равняется сумме постояннойb
и бесконечно малой функции
равняется сумме постояннойb
и бесконечно малой функции
![]() ,
т. е.
,
т. е.![]() ,
где
,
где![]() при
при![]() ,
то эта постоянная является ее пределом,
т. е.
,
то эта постоянная является ее пределом,
т. е.![]() .
.
Д
о к а з а т е л ь с т в о. Пусть
![]() ,
,![]() .
.
Отсюда
следует
![]() .
В самом деле
.
В самом деле![]()
![]() ,
т. е.
,
т. е.
![]() .
.
1.7. Теоремы о пределах (свойства пределов)
Теорема 1.5. Предел суммы конечного числа функций равен сумме пределов этих функций, т. е.
![]() .
.
Д о к а з а т е л ь с т в о. Используем теорему 1.3.
![]() ,
,
![]() ,
,
………………………………………..
![]() ,
,
где
![]()
бесконечно малые функции при
бесконечно малые функции при
![]() .
.
Сумму левых частей равенств приравняем сумме правых частей, получим
![]() .
Так как сумма
.
Так как сумма
![]() является постоянной, а сумма конечного
числа бесконечно малых функций
является постоянной, а сумма конечного
числа бесконечно малых функций![]()
бесконечно малой функцией по первому
свойству бесконечно малых функций, то
по теореме 1.4
бесконечно малой функцией по первому
свойству бесконечно малых функций, то
по теореме 1.4
![]()
![]()
![]() .
.
Теорема
1.6. Предел
произведения функций равен произведению
пределов этих функций, т. е.
![]() .
.
Д
о к а з а т е л ь с т в о. Пусть существуют
пределы
![]() и
и
![]() .
По теореме 1.3
.
По теореме 1.3
![]() ,
,![]() ,
где
,
где![]()
постоянные величины,
постоянные величины,![]()
бесконечно малые функции при
бесконечно малые функции при
![]() .
Тогда
.
Тогда![]()
![]() .
.
Так
как сумма
![]() является постоянной величиной, а
является постоянной величиной, а![]() является бесконечно малой функцией по
свойствам 1 и 2 бесконечно малых функций,
то по теореме 1.4
является бесконечно малой функцией по
свойствам 1 и 2 бесконечно малых функций,
то по теореме 1.4
![]() .
.
Следствие 1. Постоянную величину можно выносить за знак предела, т.е.
![]() .
.
Следствие
2. Предел
степени функции равен степени предела
функции, т. е.
![]() .
.
Теорема 1.7. Предел частного функций равен частному пределов функций, если предел функции, стоящей в знаменателе, отличен от нуля, т. е.
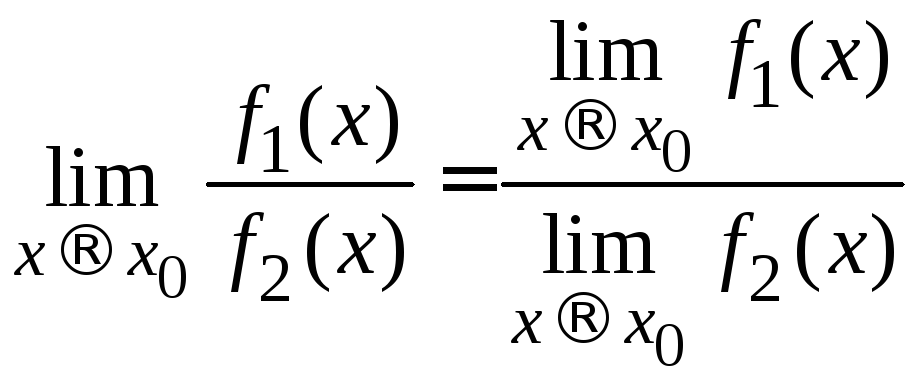 .
.
Д
о к а з а т е л ь с т в о. Пусть
![]() ,
,![]() ,
,![]() .
.
На
основании теоремы 1.3 имеем
![]() ,
,![]() .
.
Найдем
разность функции
![]() и постоянной
и постоянной![]() .
.
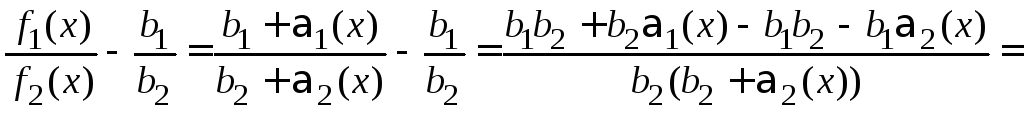
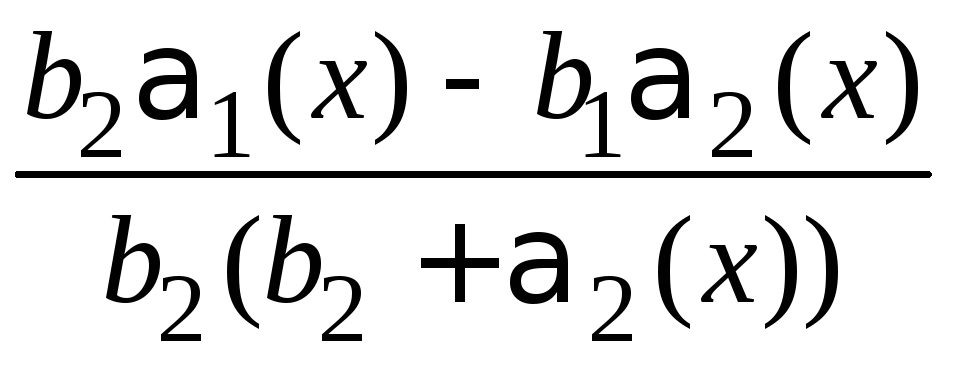 .
.
Согласно
свойствам бесконечно малых функций
данная разность является бесконечно
малой функцией, следовательно, по теореме
1.4 предел функции
![]() равняется постоянной
равняется постоянной![]() ,
т. е.
,
т. е.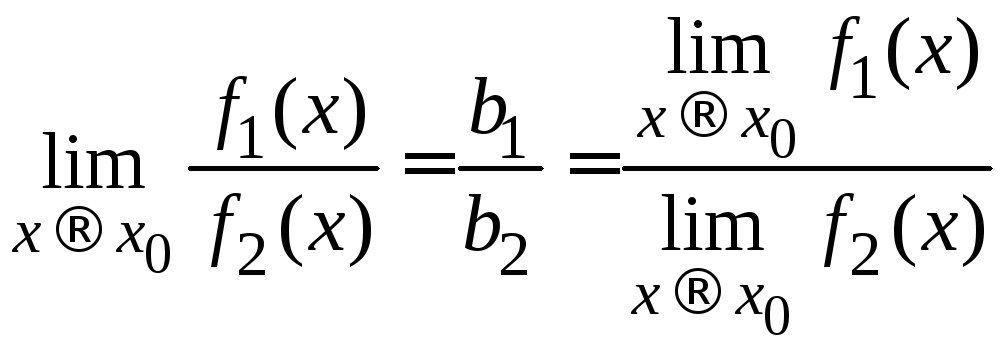 .
.
1.8. Замечательные пределы
При
нахождении пределов от функций, являющихся
частным двух других функций, часто
возникают случаи, когда предел и
числителя, и знаменателя равняется нулю
или бесконечности. Данные случаи
называются неопределенностями типа
частного вида
![]() и
и![]() .
При нахождении пределов могут также
встречаться неопределенности типа
степени. Например, таких видов:
.
При нахождении пределов могут также
встречаться неопределенности типа
степени. Например, таких видов:![]() .
В этих случаях нельзя сразу с помощью
подстановки предельного значения
независимой переменной в функцию найти
предел или утверждать, что этот предел
не существует. Необходимо применять
специальные приемы и формулы. Замечательные
пределы служат для раскрытия
неопределенностей типа частного
.
В этих случаях нельзя сразу с помощью
подстановки предельного значения
независимой переменной в функцию найти
предел или утверждать, что этот предел
не существует. Необходимо применять
специальные приемы и формулы. Замечательные
пределы служат для раскрытия
неопределенностей типа частного![]() и специального вида неопределенности
типа степени
и специального вида неопределенности
типа степени![]() .
.
1.8.1. Первый замечательный предел
Теорема 1.8 о промежуточной функции.
Если
в некоторой -окрестности
точки
![]()
![]() значения функции
значения функции![]() заключены между значениями функций
заключены между значениями функций![]() и
и![]() ,
т. е.
,
т. е.![]()
![]()
![]() и при этом
и при этом![]() =b,
то
=b,
то
![]() .
.
Д
о к а з а т е л ь с т в о. Пусть
![]() .
.
Тогда
![]()
![]()
![]() ,
,
![]()
![]()
![]() .
.
Выберем
![]() ,
тогда
,
тогда

![]() .
.
Теорема 1.9 о первом замечательном пределе.
Для
любой бесконечно малой функции
![]() предел отношения
предел отношения равен единице, т. е.
равен единице, т. е.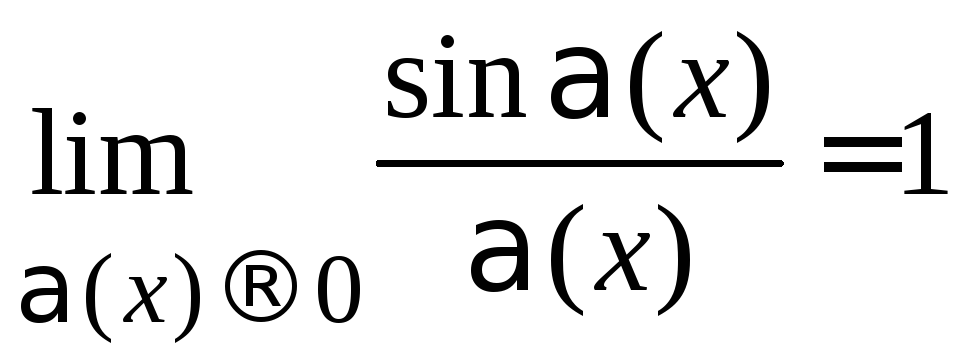 .
(1.1)
.
(1.1)
Д о к а з а т е л ь с т в о. Рассмотрим окружность радиуса R с центром в точке О, сектор OAB с углом и треугольники OAB, OAС, (АС – касательная к окружности) (рис. 8).
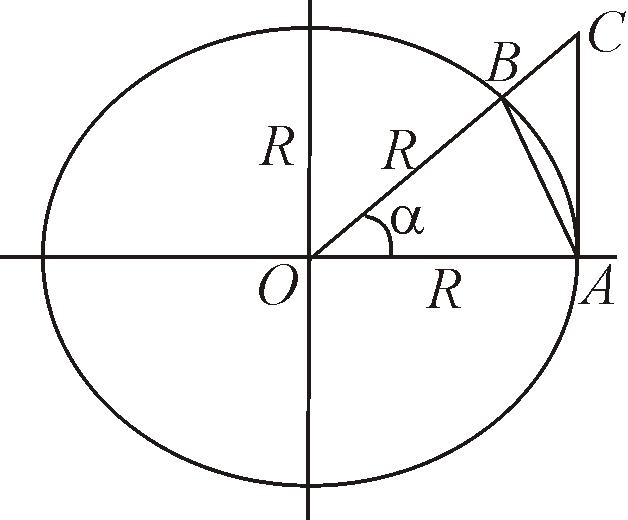
Рис. 8
Очевидно, для площадей этих фигур справедливо соотношение
![]() .
.
Площади треугольников и сектора найдем по известным формулам, получим
![]() .
.
Умножим
данное неравенство на
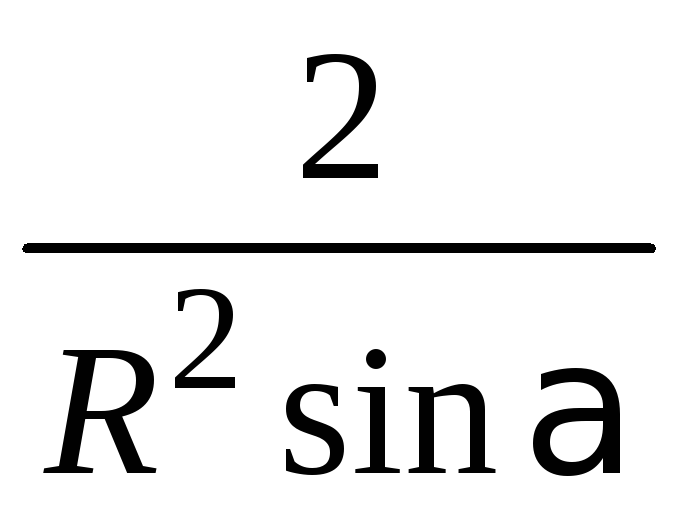 ,
имеем
,
имеем![]() .
.
Для обратных величин этого неравенства справедливо соотношение
![]() .
.
Так
как
![]() ,
то по теореме о промежуточной функции
,
то по теореме о промежуточной функции
![]() .
.
Бесконечно
малые функции, предел отношения которых
равен единице, называются эквивалентными.
Записывают
![]()
.
.
Пример
1.5.
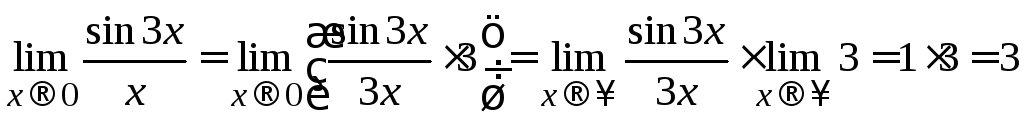 .
.
Пример
1.6.
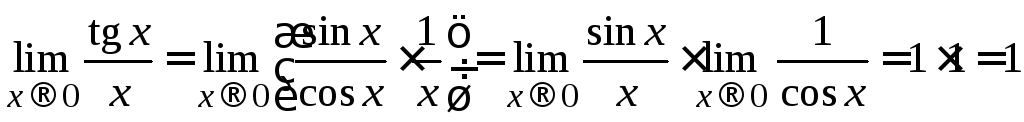 .
.
Это значит, что tgx и х являются эквивалентными функциями (tgx х).
Пример 1.7.
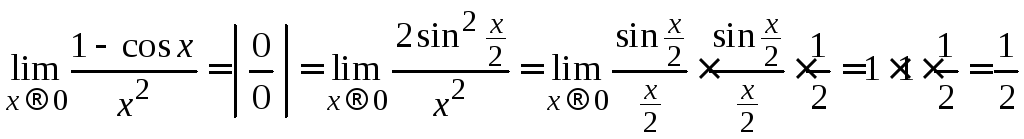 .
.
