1.2. Функции, их классификация

Одним из основных понятий математического анализа является функция.

Зачатки определения функции имелись у П. Ферма и Б. Паскаля. Впервые слово функция употребил Лейбниц в 1692 г.

Определение функции, наиболее близкое к современному, дал И. Бернулли в 1718 г.

До недавнего времени наиболее распространенным было следующее определение функции.

Переменная величина y называется функцией переменной величины x, если каждому значению х соответствует единственное определенное значение y. Записывается .

В настоящее время обычно употребляют определение функции, основанное на теории множеств.

Переменная величина y называется функцией переменной величины x с областью определения D и множеством значений E, если для любого значения х, принадлежащего множеству D ( x  D) существует единственное значение y, принадлежащее множеству Е (y  E) (рис. 3), т. е.

.

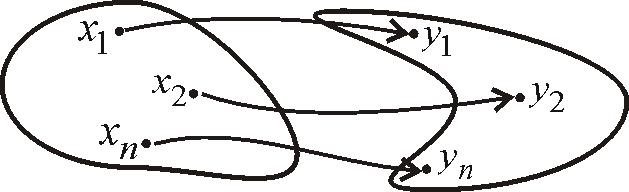
Рис. 3

Например, найти область определения и множество значений функции 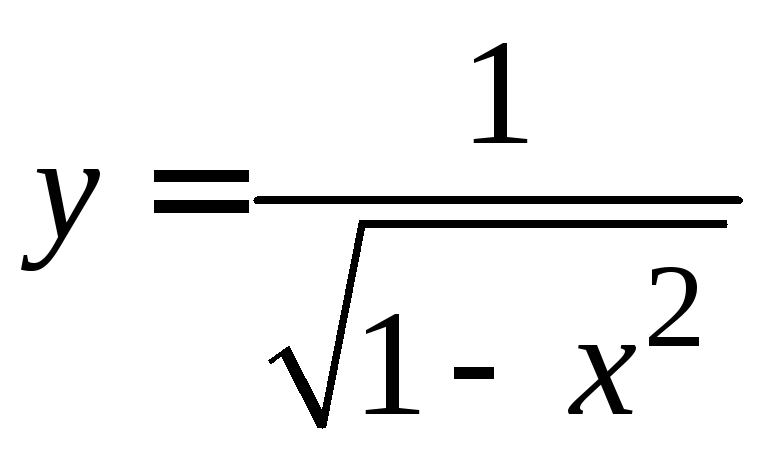. Получаем,.

Если между множествами D и E можно установить взаимно однозначное соответствие, то существует обратная функция или.

Если аргумент функции является в свою очередь функцией переменной величиных , тоназываетсясложной функцией.

Здесь функции иназываются составляющими функциями.

Например, сложная функция, ее составляющие функциии.

Основными элементарными функциями являются следующие:

1)  степенная функция;

2)  показательная функция;

3)  логарифмическая функция;

4)  тригонометрические функции;

5)  обратные тригонометрические функции.

Функция называется элементарной, если она образована из основных элементарных с помощью конечного числа алгебраических действий: сложения, вычитания, умножения, деления, возведения в рациональную степень.

Например, .

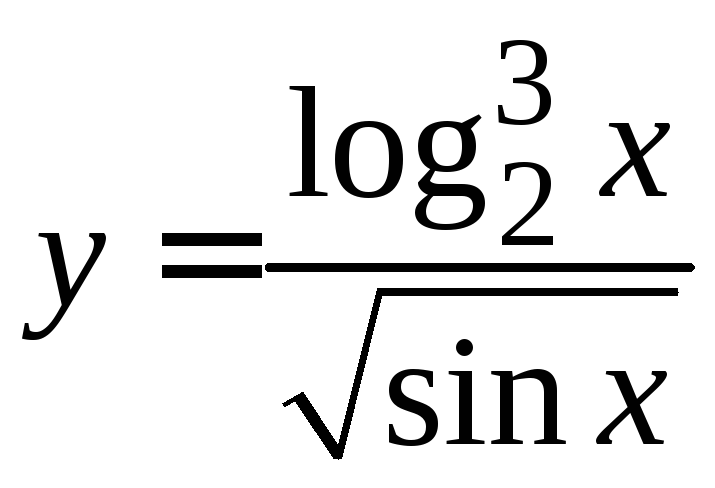Функция называется алгебраической, если она образована из независимой переменной x с помощью конечного числа алгебраических действий: сложения, вычитания, умножения, деления, возведение в степень с рациональным показателем.

Функция называется трансцендентной, если она не является алгебраической.

Алгебраическая функция называется иррациональной, если она содержит операцию извлечение корня.

Функция называется рациональной, если она является алгебраической и не содержит корней независимой переменной.

Простейшей рациональной функцией является многочлен вида

,

где – числовые коэффициенты,х – независимая переменная, n – целое положительное число.

Любую рациональную функцию можно представить в виде отношения двух многочленов

,

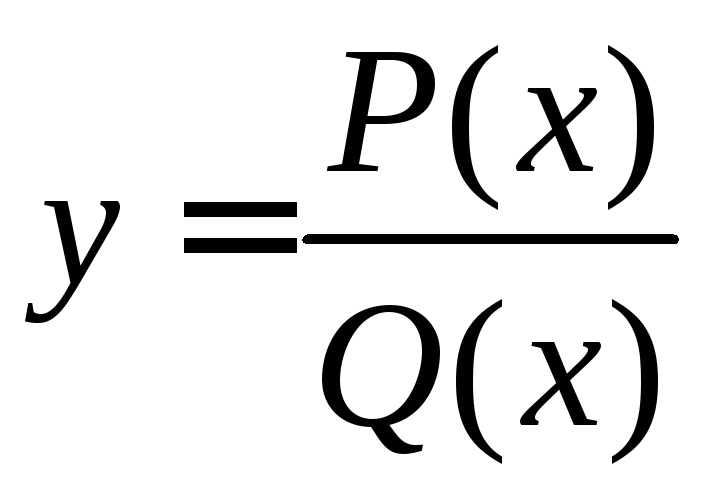где ,– числовые коэффициенты,m – целое положительное число.

1.3. Предел последовательности

Окрестностью точки называется любой интервал, содержащий эту точку.

-окрестностью точки называется интервал длиной 2 с центром в этой точке.

В математическом анализе обычно рассматривается -окрестность точки , которая не содержит точку(рис. 4).

Кратко записывается

или .

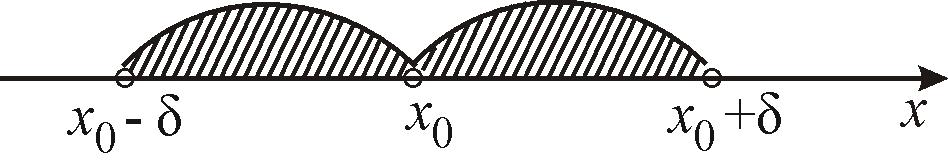
Рис. 4

Пусть в некоторой области D имеется предельная точка .

Точка называется предельной, если любая, сколь угодно малая, ее окрестность содержит бесконечное множество точек этого множества. Из любого бесконечного множества точек можно выбрать бесконечное счетное множество, т.е. последовательность . Пусть эта последовательность такая, что с увеличением номераn члены последовательности неограниченно приближаются к, но никогда не достигают его. Так что расстояние от точких до точки становится сколь угодно мало, но никогда не становится равным нулю. В этом случае говорят, что члены последовательностистремятся к. Стремятся к– значит неограниченно приближаются, но не достигают(рис. 5).

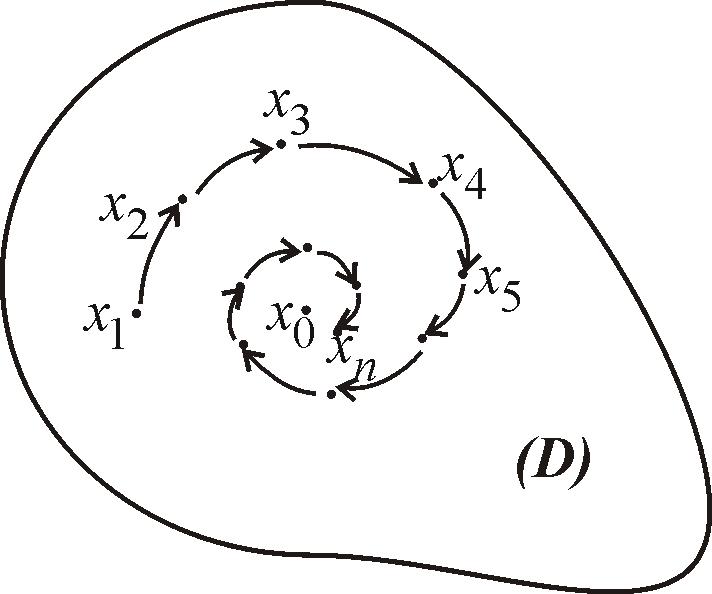
Рис. 5

Определение предела последовательности. Число b называется пределом последовательности (), если для любого, сколь угодно малого, положительного существует такое положительное число N, что если номер члена последовательности n > N, то принадлежит-окрестности числа b ().

Кратко с помощью кванторов можно записать

.

Например, доказать, что . Запишем последнее соотношение из определения предела и преобразуем его, учитывая, что, аb = 0. Получим . Отсюда следует, что для того, чтобы член последовательностиотличался от пределаb = 0 меньше, чем на  = 0,001, его номер n должен быть больше (n > 1000). При  = 0,0001 N() равняется и т. д. Таким образом, для любого можно выбрать N() такое, что , если толькоn > N(). Следовательно, предел этой последовательности равен нулю.

Теорема Больцано-Коши (без доказательства). Для того, чтобы последовательность имела предел, необходимо и достаточно, чтобы для любого > 0 существовало N()> 0 такое, что если n > N, m > N, то .

Теорема Вейерштрасса (без доказательства). Если последовательность монотонно возрастает (убывает) и ограничена сверху (снизу), то она имеет предел.

Последовательность называется монотонно возрастающей (убывающей), если для любогоn  N ().