
- •В. Г. Шершнев математический анализ
- •Часть I. Дифференциальное исчисление
- •Оглавление
- •Календарно-тематический план Распределение часов по темам и видам работ
- •Глава I. Введение в математический анализ
- •1.1. Множества
- •1.1.1. Определение множества
- •1.1.2. Операции над множествами
- •1.1.3. Свойства операций над множествами
- •1.1.4. Декартово произведение множеств
- •1.1.5. Модуль числа, его свойства
- •1.1.6. Грани числовых множеств
- •1.1.7. Счетные и несчетные множества
- •1.2. Функции, их классификация
- •1.3. Предел последовательности
- •1.4. Предел функции
- •1.4.1. Определение предела функции
- •1.4.2. Геометрический смысл предела
- •1.4.3. Односторонние пределы. Необходимое и достаточное условия существования предела функции
- •1.5. Бесконечно малые и бесконечно большие функции
- •1.5.1. Определение бесконечно малой и бесконечно большой функций
- •1.5.2. Свойства бесконечно малых функций
- •1.6. Теоремы о представлении функции в виде суммы предела и бесконечно малой функции
- •1.7. Теоремы о пределах (свойства пределов)
- •1.8. Замечательные пределы
- •1.8.1. Первый замечательный предел
- •1.8.2. Второй замечательный предел
- •1.8.3. Применение второго замечательного предела в финансовых вычислениях
- •1.9. Сравнение бесконечно малых функций
- •1.10. Непрерывность функции в точке и на отрезке
- •1.10.1. Определение непрерывности функции
- •1.10.2. Действия над непрерывными функциями
- •1.10.3. Непрерывность элементарных функций
- •1.10.4. Свойства непрерывных функций
- •1.10.5. Точки разрыва функций
1.5. Бесконечно малые и бесконечно большие функции
1.5.1. Определение бесконечно малой и бесконечно большой функций
Определение
бесконечно малой функции.
Функция (x)
называется бесконечно малой функцией
при
![]() ,
если для любого сколь угодно малого
положительного числа
существует такое положительное число
,
зависящее от ,
что для любого x,
принадлежащего
-окрестности
,
если для любого сколь угодно малого
положительного числа
существует такое положительное число
,
зависящее от ,
что для любого x,
принадлежащего
-окрестности
![]()
![]() (x)
находится в -окрестности
начала координат (x)
(x)
находится в -окрестности
начала координат (x)![]() ,
т.е.
,
т.е.![]() .
.
В краткой записи на языке « » данное определение имеет вид
![]()
![]()
![]() .
.
Ни
какое малое число (например,
![]() и
т. д.) не является бесконечно малой
величиной, кроме числа
и
т. д.) не является бесконечно малой
величиной, кроме числа![]() .
.
Определение
бесконечно большой функции.
Функция
![]() называется бесконечно большой при
называется бесконечно большой при![]() ,
если для любого сколь угодно большого
положительного числаN
существует такое положительное число
,
если для любого сколь угодно большого
положительного числаN
существует такое положительное число
![]() ,
зависящее отN,
что если x
принадлежит -окрестности
числа
,
зависящее отN,
что если x
принадлежит -окрестности
числа
![]() (
(![]() ),
то абсолютная величина значения
функции больше числаN
(
),
то абсолютная величина значения
функции больше числаN
(
![]() ),
т.е.
),
т.е.![]() .
.
Иначе, можно кратко записать
![]()
![]()
![]() .
.
Теорема 1.2. Функция, обратная по величине к бесконечно малой функции является бесконечно большой и, наоборот, функция, обратная по величине к бесконечно большой, является бесконечно малой функцией.
Д о к а з а т е л ь с т в о.
1.
Пусть (x)
бесконечно малая функция, т. е.
![]() .
Докажем, что
.
Докажем, что![]() является бесконечно большой, т. е.
является бесконечно большой, т. е.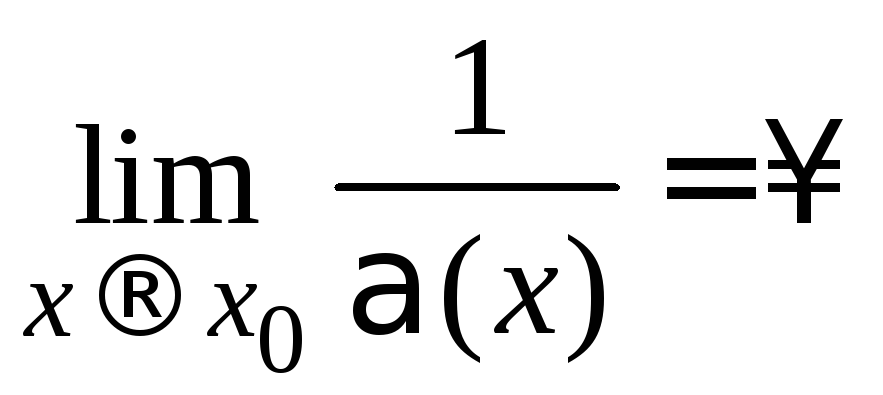 .
ПустьN
произвольно выбранное сколь угодно
большое положительное число. Так как
.
ПустьN
произвольно выбранное сколь угодно
большое положительное число. Так как
![]() ,
то для любого,
в том числе и для
,
то для любого,
в том числе и для
![]() >0,
существует такая-окрестность
>0,
существует такая-окрестность
![]() ,
что
,
что![]()
![]() ,
т. е.
,
т. е.![]() .
Однако,
.
Однако,![]() равносильно
равносильно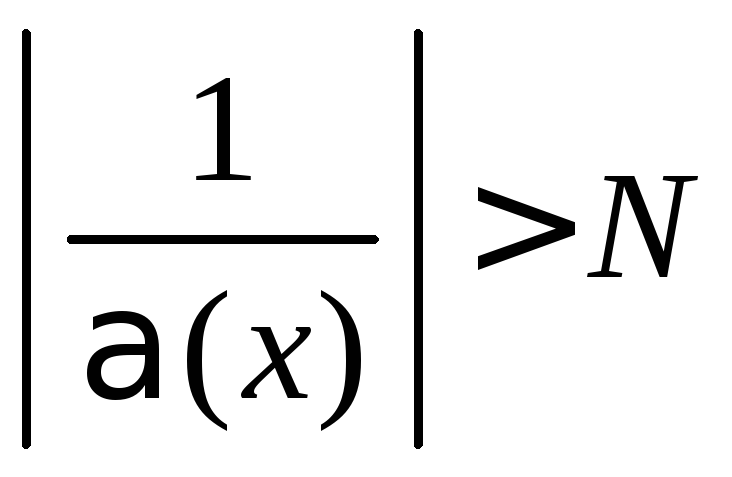 .
Следовательно, для значенийх,
принадлежащих таким образом выбранной
окрестности
.
Следовательно, для значенийх,
принадлежащих таким образом выбранной
окрестности
![]() ,
функция
,
функция![]() по абсолютной величине больше произвольно
выбранного сколь угодно большого числаN,
а это означает, что
по абсолютной величине больше произвольно
выбранного сколь угодно большого числаN,
а это означает, что
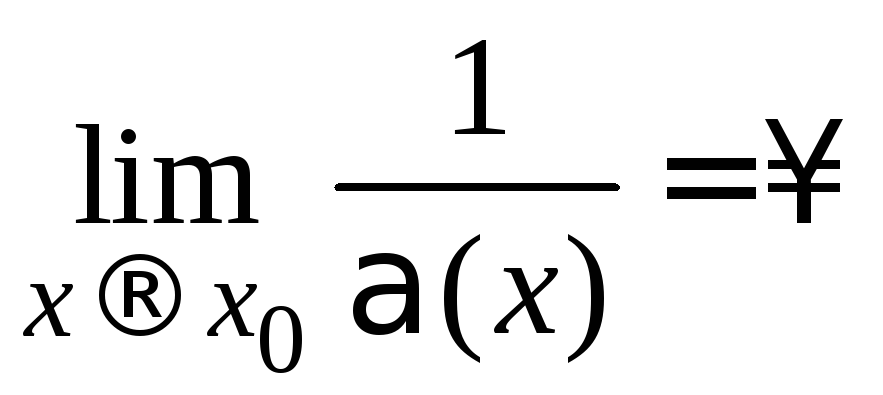 .
.
2.
Пусть
![]() .
Докажем, что
.
Докажем, что![]() является бесконечно малой функцией,
т.е.
является бесконечно малой функцией,
т.е.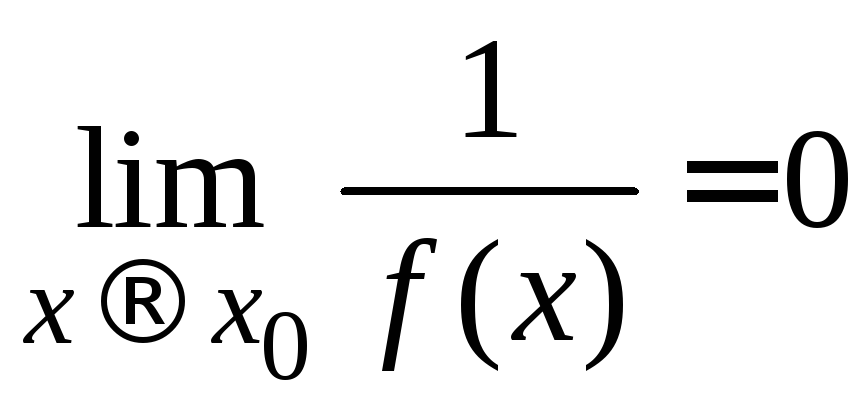 .
Так как
.
Так как![]() ,
то для любогоN,
в том числе и для
,
то для любогоN,
в том числе и для
![]() >0,
где
произвольно выбранное сколь угодно
малое положительное число, существует
такая -окрестность
>0,
где
произвольно выбранное сколь угодно
малое положительное число, существует
такая -окрестность
![]() ,
что
,
что![]()
![]() .
Однако,
.
Однако,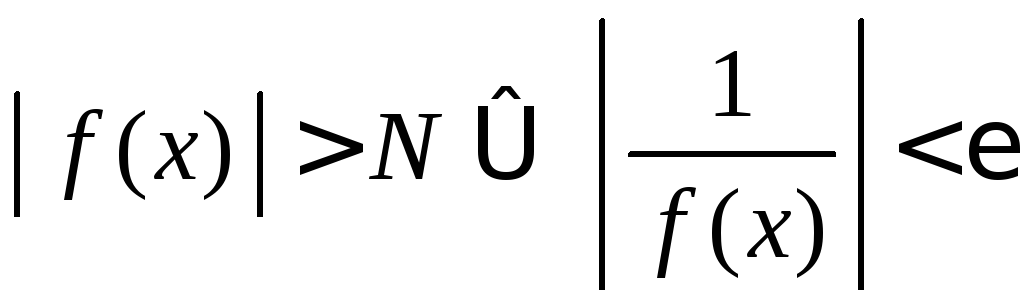 .
Следовательно, для значенийх,
принадлежащих таким образом выбранной
окрестности
.
Следовательно, для значенийх,
принадлежащих таким образом выбранной
окрестности
![]() ,
функция
,
функция![]() по абсолютной величине меньше произвольно
выбранного числа,
а это означает, что
по абсолютной величине меньше произвольно
выбранного числа,
а это означает, что
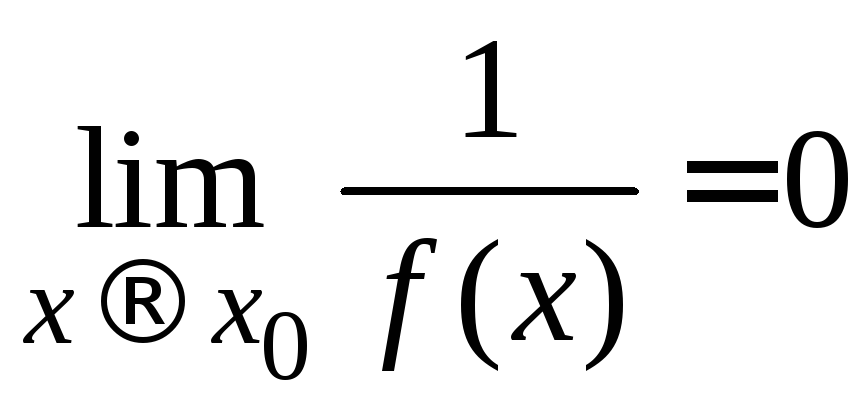 .
.
Например,
если
![]() ,
то
,
то![]() ,
и наоборот, если
,
и наоборот, если![]() ,
то
,
то![]() .
.
Данная теорема часто используется при нахождении пределов дробно-рациональных функций.
1.5.2. Свойства бесконечно малых функций
Свойство 1. Сумма конечного числа бесконечно малых функций является бесконечно малой функцией.
Д о к а з а т е л ь с т в о.
Пусть![]() бесконечно малые
функции при
бесконечно малые
функции при
![]() .
.
По определению для этих бесконечно малых функций запишем:

![]() ;
;
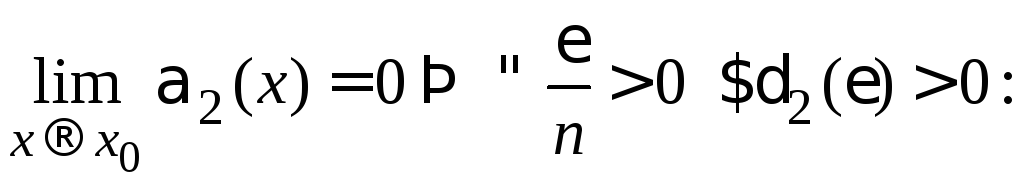
![]() ;
;
………………………………………………………………………………………..
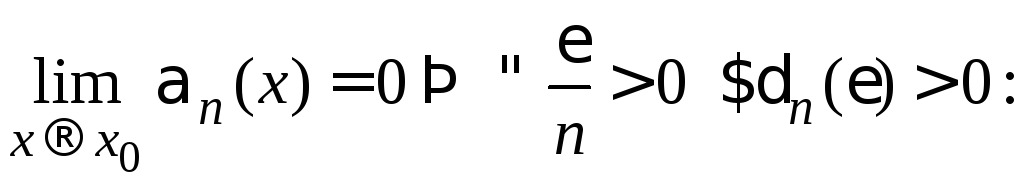
![]() .
.
Если
принять
![]() ,
то
,
то![]() имеет место неравенство:
имеет место неравенство:
![]() ,
,
т.
е. сумма бесконечно малых функций ![]() является бесконечно
малой функцией.
является бесконечно
малой функцией.
Свойство
2. Произведение бесконечно малой функции
![]() на ограниченную функцию
на ограниченную функцию![]() является бесконечно малой функцией.
является бесконечно малой функцией.
Д
о к а з а т е л ь с т в о. Пусть (х)
бесконечно малая функция, т. е.
![]() ,
а функцияf(x)
в окрестности точки
,
а функцияf(x)
в окрестности точки
![]() ограничена, т. е.
ограничена, т. е.
![]() ,
где
,
где![]() .
Так как
.
Так как![]()
бесконечно малая функция, то как бы
мало ни было число ,
в том числе и равное
бесконечно малая функция, то как бы
мало ни было число ,
в том числе и равное
![]() ,
существует такая-окрестность
,
существует такая-окрестность
![]() ,
что
,
что![]() .
.
Поэтому
![]()
![]() .
.
Следствие
1. Произведение
бесконечно малой функции
![]() на постоянную величинуС
является бесконечно малой функцией, т.
е.
на постоянную величинуС
является бесконечно малой функцией, т.
е.
![]() .
.
Следствие
2. Произведение
бесконечно малых функций
![]() и
и![]() является бесконечно малой функцией.
является бесконечно малой функцией.
Свойство
3. Частное от деления бесконечно малой
функции
![]() на функцию
на функцию![]() ,
предел которой отличен от нуля (
,
предел которой отличен от нуля (![]() )
является бесконечно малой функцией.
)
является бесконечно малой функцией.
Д о к а з а т е л ь с т в о. Пусть (x) бесконечно малая функция, т. е.
![]() и
и
![]() .
Докажем, что
.
Докажем, что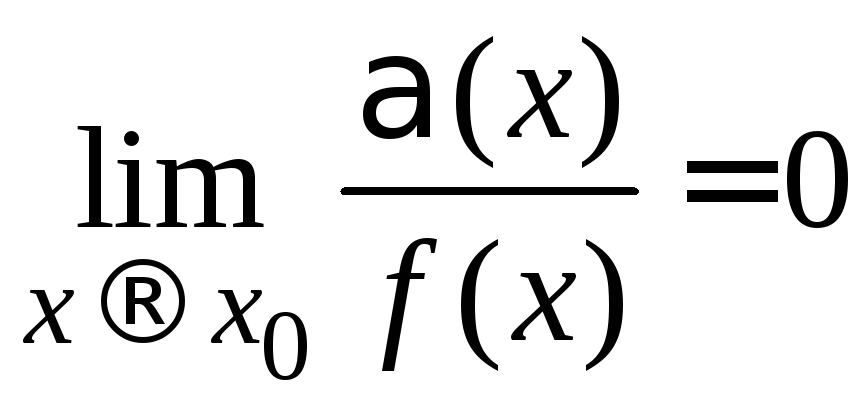 .
.
Так
как
![]() ,
то существует такая-окрестность
,
то существует такая-окрестность
![]() ,
что
,
что![]()
![]() ,
а следовательно
,
а следовательно .
Это значит, что в-окрестности
точки
.
Это значит, что в-окрестности
точки
![]() функция
функция![]() ограничена. По свойству 2 произведение
бесконечно малой(x)
на ограниченную функцию
ограничена. По свойству 2 произведение
бесконечно малой(x)
на ограниченную функцию
![]() является бесконечно малой, т. е.
является бесконечно малой, т. е.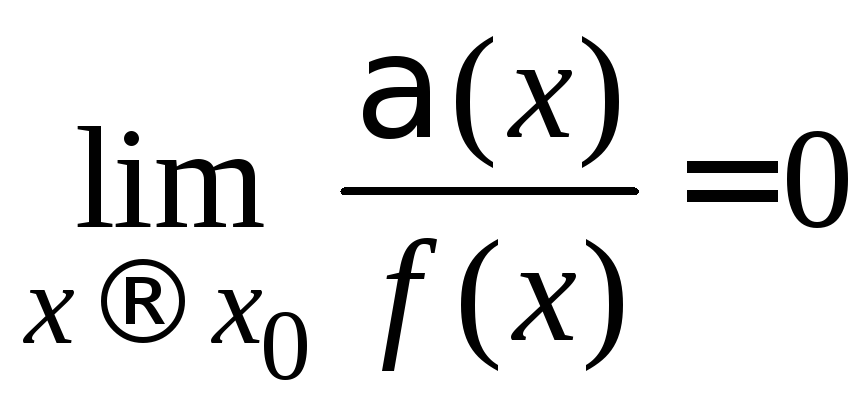 .
.
