xi+1 = xi + h

,

Следующие расчетные формулы приводятся без вывода.

y

y(x)

У

y1

A

П

y0

o

α

Т

B

Н .

y(x −

x)

h

α

И

x0

x

x1

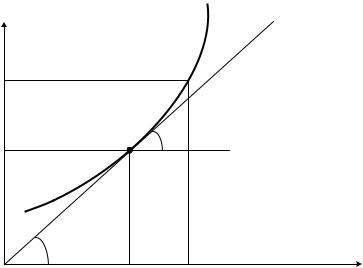
Рис. 2.4. Графический вид метода Эйлера

Н

.

Э

И

Ю

Модифицированный метод Эйлера ( ариант 1)

у О= у + hf(x +h / 2,вy +hf(x ,y

) / 2),

i+1

i

i

i

i i

Э

о

xi+1= xi+h.

МодифицировП

н

нный метод Эйлера (вариант 2)

Э

с

уi+1 = уi+(h/2)[f(xi,yi)+f(xi+h,yi+hf(xi,yi))],

а

.

xi+1=xi+h.

ц

р

К

1.3.2. Метод Рунге-Кутта

о

Метод Рунге-Кутта третьего порядка

уi+1=уi+(k1+4k2+k3)/6,

11

k1=hf(xi, yi),

,

k2=hf(xi+h/2, yi+k1/2),

У

k3=hf(xi+h, yi+2k2 - k1),

П

Т

xi+1=xi+h.

Метод Рунге-Кутта четвертого порядка

.

Н

уi+1=уi+(k1+2k2+2k3+k4)/6,

И

k1=hf(xi,yi),

Ю

Н

k2=hf(xi+h/2, yi+k1/2),

.

Э

k3=hf(xi+h/2, yi+k2/2),

k4=hf(xi+h, yi+k3),

И

xi+1=xi+h,

где у

П

функции

т чках x

, x

соответственно,

с

i+1

i

в i+1

i

индекс i показывает номер шага

тегрир вания, h – шаг интегрирова-

ния. НачальныеЭусловия при чи

омле интегрировании учитываются

Э

а

на нулевом шаге: i = 0, x = x0, y = y0.

.

2

ц

Пример

Численно и аналитически решить дифференциальное уравнение

о

dy/dx=x

при y|

=1. Определить значение функции при x

= 1, h = 1.

x=р0

k

РешениеКзадачи

dy/dx = x2

y

x

∫dy = ∫x2dx.

1

0

12