БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ВОЕНМЕХ» им. Д. Ф. УСТИНОВА

Кафедра систем обработки информации и управления

В.Ю. Емельянов

УПРАВЛЕНИЕ В ТЕХНИЧЕСКИХ СИСТЕМАХ

Конспект лекций

Санкт-Петербург

2008

	СОДЕРЖАНИЕ		стр.
	Лекция 1. Основные понятия теории автоматического управления, виды
задач управления, фундаментальные принципы управления. Показатели
качества управления. Базовый пример системы управления . . . .			3
Лекция 2. Передаточные функции и частотные характеристики динами-
ческих звеньев и систем . . . . . . . . . . . . . .			7
Лекция 3. Структурно-динамическая схема системы. Типовые соедине-
ния динамических звеньев. Передаточные функции замкнутых систем			9
Лекция 4. Основные положения теории устойчивости. Алгебраические
методы анализа устойчивости линейных систем управления		. . .	13
Лекция 5. Частотные методы анализа устойчивости систем управления			15
Лекция 6. Оценка точности систем управления. Понятия астатизма и ин-
вариантности . . . . . . . . . . . . . . . .			21
Лекция 7. Назначение, принципы построения и основные особенности
компьютерных систем управления . . . . . . . . . . .			23
Лекция 8. Математическая модель импульсного элемента. Решетчатые
функции и разностные уравнения . . . . . . . . . . .			26
Лекция 9. Дискретные преобразования и их свойства . . . . .			29
Лекция 10. Передаточные функции импульсных звеньев и систем . .			34
Лекция 11. Анализ устойчивости и качества импульсных систем . .			37
Лекция 12. Особенности построения математических моделей компью-
терных систем управления. Методы линеаризации . . . . . .			43
Лекция 13. Передаточные функции компьютерных систем управления			48
Лекция 14. Синтез системы управления. Обеспечение точности системы			52
Лекция 15. Синтез системы управления. Обеспечение запаса устойчиво-
сти системы . . . . . . . . . . . . . . . . .			55
Лекция 16. Синтез системы управления. Обеспечение запаса устойчиво-
сти системы (продолжение) . . . . . . . . . . . . .			59
Лекция 17. Применение типовых ЛАХ при синтезе цифровых систем
управления . . . . . . . . . . . . . . . . .			62
.
Лекция 18. Непрерывные корректирующие звенья . . . . . .			65
Лекция 19. Синтез непрерывных корректирующих средств . . . .			71
Лекция 20. Синтез компьютерного управления . . . . . . .			72
Лекция 21. Постановка задачи оптимального управления . . . .			76
Лекция 22. Синтез оптимального управления на основе вариационного
исчисления . . . . . . . . . . . . . . . . .			79
Лекция 23. Синтез линейного регулятора, оптимального по квадратич-
ному критерию . . . . . . . . . . . . . . . .			83
Лекция 24. Каноническая форма уравнений Эйлера. Принцип максиму-
ма	. . . . . . . . . . . . . . . . . . .		86
.

2

Лекция 25. Синтез системы стабилизации, оптимальной по быстродей-

ствию . . . . . . . . . . . . . . . . . . . 89

.

3

Лекция 1. Основные понятия теории автоматического управления, виды задач управления, фундаментальные принципы управления. Показатели качества управления. Базовый пример системы управления

Управление - это воздействие на объект с целью обеспечения требуемого течения процесса в объекте или требуемого изменения его состояния.

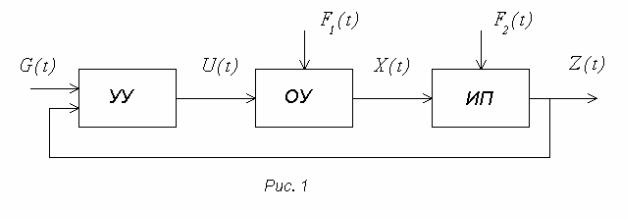
На рис. 1: ОУ - объект управления, УУ - устройство управления (регуля- тор), ИП - измерительная подсистема, G - задающее воздействие (требуемое состояние ОУ), X - текущее состояние ОУ (вектор переменных состояния), Z - измеренный вектор состояния, U - сигнал управления (вектор управления), F1 - вектор возмущающих воздействий, F2 - вектор шумов (помех) измерения.

Основные виды задач управления:

-стабилизация (регулирование) G=const;

-программное управление G=G( t);

-слежение (сопровождение, наведение) G = X ц (t), где X ц (t) - состояние

другого объекта (цели);

-терминальное управление - требуется обеспечить заданное состояние объекта в определенный (конечный) момент времени T;

-экстремальное управление - в процессе управления требуется обеспе- чить максимум или минимум некоторых характеристик, например, при про- граммном управлении обеспечить минимальный расход топлива.

Решение указанных задач управления основано на использовании в раз- ных вариантах двух фундаментальных принципов: принципа обратной связи и принципа компенсации возмущений.

Принцип обратной связи состоит в сравнении текущего состояния объек- та управления X с требуемым G и формировании сигнала управления на основе различия между ними. Основной и простейший вариант реализации данного принципа - единичная отрицательная обратная связь (рис. 2). На входе УУ

формируется разность x(t) = g(t) − y(t), где y - выходной сигнал системы, характеризующий ее состояние, x - сигнал ошибки. Другие варианты обратной

4

связи: неединичная, гибкая, положительная применяются для повышения каче- ства процесса управления.

Принцип компенсации возмущений состоит в формировании сигнала управления с учетом как величины задающего воздействия, так и

величины возмущающих воздействий (рис. 3).

Благодаря этому может быть обеспечена высокая точность системы управления, но реализация

этого принципа затруднена необходимостью точного измерения произвольно из-

меняющихся возмущающих воздействий. На практике данный принцип применя- ется, как правило, в сочета-

нии с принципом обратной связи.

В теории управления рассматриваются два ос- новных класса задач: зада-

чи анализа и синтеза систем управления. Задачи анализа сводятся к оценке устойчивости и качества системы. Задачи синтеза - к обеспе-

чению у проектируемой системы указанных свойств.

Показатели качества систем управления можно разделить на четыре ос- новные группы:

-показатели точности,

-показатели быстродействия,

-показатели запаса устойчивости,

-комплексные показатели качества.

В конкретных практических задачах могут вводиться другие виды пока- зателей качества.

Рассмотрим пример системы самонаведения летательного аппарата (ЛА). На рис. 4: Xц = (xц , yц ,zц ) - вектор линейных координат цели (Ц); К - коор-

динатор, формирующий сигнал самонаведения σ; УУ - устройство управления (автопилот и рулевые машины), формирующее вектор управляющих сигналов

для ЛА δ = (δв ,δн ,δэ ) на основе σ и вектора измеренных координат ЛА Z; X - вектор линейных и угловых координат ЛА; ИП - измерительная подсистема.

5

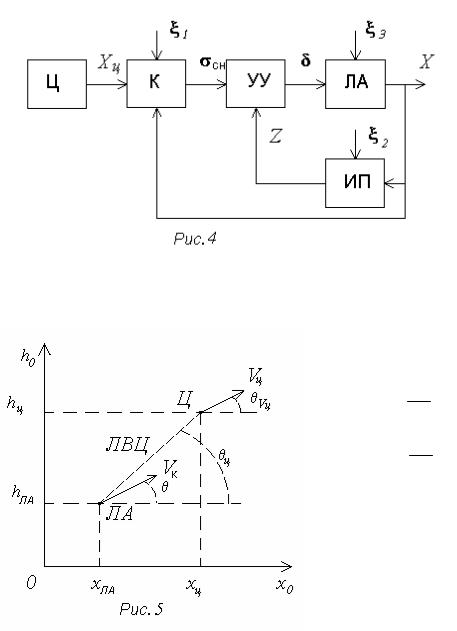
Отметим, что в процессе управления ЛА необходимо параллельно решать две задачи управления: обеспечивать стабилизацию углового положения ЛА и наведение на цель. Соответственно на рис. 4 показаны два контура управления.

Задачи управ- ления здесь прихо- дится решать при на-

личии возмущающих воздействий: ξ1 - ес-

тественные и органи-

зованные помехи для

координатора;

ξ 2 -

шумы измерений для информационной

подсистемы;

ξ 3 -

внешние силы и мо-

менты, действующие на ЛА (ветер и др.).

Составим математическую модель системы, ограничиваясь вертикальной плоскостью (рис. 5). Текущие значения линейных координат ЛА можно опре- делить из дифференциальных уравнений:

dxdt = V cos θ + ux , dydt = V sin θ + uy ,

где V - скорость ЛА, θ - угол наклона траектории ЛА, ux , uy - составляющие

скорости ветра. Аналогичные уравнения можно записать для координат цели.

Угол наклона траектории,

характеризующий направление движения ЛА, формируется в процессе его углового движения, описываемого уравнениями равновесия сил и момен-

тов:

	mV	dθ	= Psin α + N − G cosθ ,	J z	d 2υ	= Mz ,
		dt			dt 2

где m - масса ЛА, P - сила тяги двигателя (рис. 6), N - подъемная (нормальная) сила, G - сила веса ЛА, υ - угол тангажа, α = υ − θ − угол атаки, Jz - момент инерции ЛА,

6

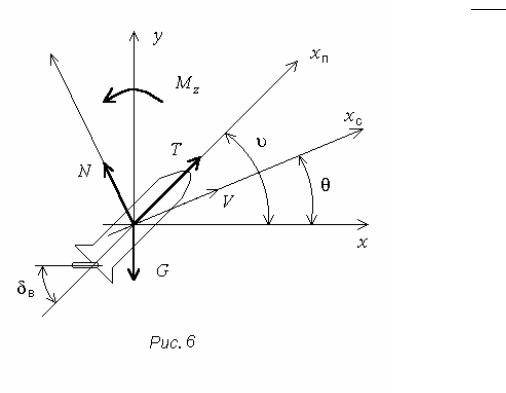
Mz = Mz æçèa,dв ,u. ö÷ø - вращающий момент, обеспечиваемый рулями высоты.

Повороты рулей высоты в первом приближении можно описать уравнением:

Tр• dδВ + dВ = kр•s, dt

где kрп , Tрп - постоянная

времени и коэффициент пере- дачи рулевого привода. Сигнал управления σ включает в себя две составляющие:

σ = σс н + σс т, сигнал стаби-

.

лизации: σс т = i1υ + i2 υ, i1,i2 - коэффициенты закона

стабилизации, сигнал самона- ведения σс н формируется в

зависимости от текущих зна-

чений координат ЛА и цели в соответствии с выбранным за- коном.

На основе рассматривае- мой впоследствии процедуры линеаризации и с учетом гипотезы о малых зна- чениях угловых координат модель рассматриваемой системы может быть полу- чена в виде следующей системы дифференциальных уравнений:

dθ

= KJ - Kq,

σ = σ

с т

+ σ

,

dt

с н

dϑ

= w

z

,

σ

с т

= i ϑ + i ω

z

,

dt

1

2

dωz

= Lq - LJ - Mw

z

- Nd

в

,

s

с н

= -k

(q

ц

- q),

dt

с н

kрп

yц − yла

dd

в

=

s -

1

dв

,

qц =

,

Tрп

Tрп

D

dt

dyц

dyла

= Vq,

= V

,

dD

= V

-V ,

dt

dt

цy

dt

цx

где ω z - скорость изменения угла тангажа ЛА, D - горизонтальная проекция

дальности "ЛА-цель", K,L,M,N - аэродинамические коэффициенты, kсн - коэф- фициент самонаведения (используется метод погони), θц - измеренный коор-

динатором угол наклона линии визирования цели.

7