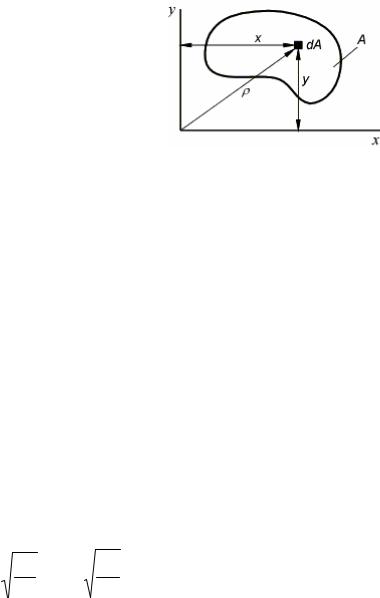
Осевыми моментами инерции сечения называются интегралы

Jx = ∫ y2dA J y = ∫ x2dA			(4.1)
A	,	A
Центробежным моментом инерции называется интеграл
Jxy	= ∫ xydA		(4.2)
	A
Полярным моментом инерции называется интеграл
Jρ	= ∫ ρ 2dA		(4.3)
	A
Так как ρ 2 = x2 + y2 , то
Jρ	= Jx	+ J y ,

т.е. полярный момент инерции сечения относительно заданной точки равен сумме осевых моментов инерции относительно двух взаимно перпендикулярных осей, проходящих через эту точку.

4.1.4. Радиусы инерции

Величины, определяемые по формулам:

ix =	J	x	; iy =	J y	, – называются радиусами инерции относительно осей x и y
				A
	A

соответственно

4.2. Основные теоремы о моментах инерции

4.2.1. Теорема о моментах инерции относительно осей, параллельных центральным

Осевой момент инерции сечения относительно произвольной оси равен моменту инерции относительно центральной оси параллельной данной плюс произведение квадрата расстояния между осями на площадь сечения.

Центробежный момент инерции сечения относительно произвольных осей координат равен центробежному моменту инерции относительно центральных осей параллельных данным плюс произведение площади сечения на расстояния между осями.

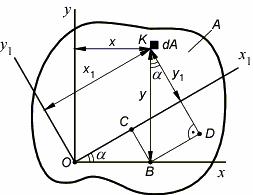
Рассмотрим сечение произвольной формы площадью A. Пусть оси x и y являются центральными (т.е. проходящими через центр тяжести сечения), и известны моменты инерции

Jx, Jy, Jxy. Требуется определить моменты инерции Jx1 , J y1 , Jx1y1 относительно осей x1 и y1, смещенных параллельно центральным осям на расстояния a и b соответственно.

44

Координаты элементарной площадки dA в системе координат (x1, y1): x1=x+b; y1=y+a.

По определению осевого момента инерции (4.1)

Jx1 = ∫( y + a)2 dA = Jx + 2a∫ ydA + a2 A ,

A A

где ∫ ydA = Sx = 0 .

A

Таким образом,

J	x1	= J	x	+ a2 A	(4.4)

Рассуждая аналогичным образом, можно получить

J	y1	= J	y	+ b2 A	(4.5)

По определению центробежного момента инерции (4.2):

Jx y		= ∫ x1 y1dA = ∫( y + a)(x + b)dA = Jxy + abA.
1	1		A
		A

4.2.2. Вычисление моментов инерций простейших фигур

Прямоугольник.

Сначала определим моменты инерции прямоугольника относительно осей x1 и y1.

Выделим на расстоянии y1 от оси x1 элементарную площадку dA высотой dy1 и шириной, равной ширине прямоугольника:

По определению осевого момента инерции (4.1)

Jx1 = ∫ y12dA.

A

Заменим интеграл по площади интегралом по высоте

h		3			h		3
Jx1 = ∫ y12bdy1	= b	y1				= bh	.
0	3				0	3

Аналогично

45

Jy1 = hb33 .

Моменты инерции относительно центральных осей x и y определим, пользуясь теоремой о моментах инерции относительно осей, параллельных центральным (4.4):

Jx = Jx1 −	h 2		bh =			bh3		bh3	bh3
		2				3	−	4 =	12 .
Аналогично
		J		=	hb3		.
			y		12

Круг.

Определим полярный момент инерции круга. Выделим на расстоянии ρ от центра круга элементарный слой dA толщиной dρ .

По определению полярного момента инерции (4.3)

Jρ	= ∫ ρ 2dA .
	A
Заменим интеграл по площади интегралом по радиусу
Jρ = d∫/ 2 ρ 2 2πρdρ = 2π d∫/ 2 ρ 3dρ = 2π		ρ 4			d / 2	=	πd 4 .
		4
0	0				0		32

Так как Jp=Jx+Jy и для круга Jx=Jy, то осевой момент инерции

	J		=	J	ρ	=	πd 4	.
		x		2			64

Прямоугольный треугольник.

Определим момент инерции треугольника относительно оси x1, совпадающей с его нижней стороной.

46

Выделим на расстоянии y1 от оси x1 элементарную площадку dA высотой dy1. Ширина площадки из подобия треугольников:

by

= b

h − y1

.

1

h

Момент инерции

h

b(h − y

)

y3

h

b y4

h

bh3

bh3

bh3

J x1 = ∫ y12dA = ∫ y12

1

dy1 = b

1

−

1

=

−

=

.

h

3

h 4

3

4

12

A

0

0

0

Относительно центральной оси

Jx

= Jx

h 2

bh

=

bh3

−

bh3

=

bh3

−

2

12

18

36

.

1

3

Аналогично для второй оси

J y

=

hb3

; J y =

hb3

.

12

36

1

4.2.3. Теорема о моментах инерции при повороте осей координат

Рассмотрим сечение произвольной формы площадью A. Пусть известны моменты инерции относительно осей x и y: Jx, Jy, Jxy. Требуется определить моменты инерции Jx1 , J y1 , Jx1y1

относительно осей x1 и y1, повернутых по отношению к осям x и y на угол α. Выделим в окрестности точки K с координатами x и y элементарную площадку dA.

Координаты площадки dA в повернутой системе координат:

x1 = OC + BD = x cosα + y sinα , y1 = KD − CB = y cosα − x sinα .

Осевые моменты инерции:

J x1 = ∫ y12dA = ∫( y cosα − x sinα )2 dA = Jx cos2 α + J y sin2 α − Jxy sin 2α ,

	A	A
J y1	= ∫ x12dA = ∫(x cosα + y sinα )2 dA = J ycos2 α + Jx sin2 α + Jxy sin 2α .
	A	A

Сложив попарно левые и правые части полученных уравнений, найдем:

J x1 + J y1 = J x + J y .

Таким образом, сумма моментов инерции относительно осей прямоугольной системы координат не изменяется при их повороте. Как было показано выше, эта сумма равна полярному моменту инерции относительно начала координат.

47