2.2. Числовые характеристики случайных величин

2.2.1. Математическое ожидание случайной величины

Закон распределения случайной величины является наиболее полной ее характеристикой. Он одновременно указывает и на значение случайной величины и на его вероятность. Однако часто в теории вероятностей и в ее приложениях большую роль играют постоянные числа, которые можно получить, используя законы распределения. В этом параграфе рассмотрим математическое ожидание или среднее значение случайной величины.

Пусть  обозначает дискретную случайную величину с рядом распределения

x_i x₁ x₂ ,…, x_n,…

p_i p₁ p₂ ,…, p_n,…

Определение. Математическим ожиданием дискретной случайной величины  называется сумма произведений возможных значений x_i на соответствующие им вероятности p_i. Будем обозначать математическое ожидание как M(). Тогда можно написать, что математическое ожидание вычисляется по формуле

M()=x₁ p₁ +x₂ p₂ +… x_n p_n +…= , (2.15)

если числовой ряд сходится абсолютно. Если числовой ряд (2.15) расходится или сходится условно, то в этом случае математическое ожидание случайной величины  не существует.

Пример 2.6. Найдем среднее число очков при одном подбрасывании правильного кубика. Используя ряд распределения из примера 2.3

x_i 1 2 3 4 5 6

p_i

по формуле (2.15) находим математическое ожидание

M()=1*+2* + 3* + 4*+ 5* + 6*=3,5.

Пример 2.7. Найдем среднее число суммы очков на двух кубиках.

Используя ряд распределения

η 2 3 4 5 6 7 8 9 10 11 12

p_i ,

получаем

M()=2+3+4+5+6+7+8+9+10+11+12==7.

Пусть  обозначает непрерывную случайную величину с плотностью вероятности f(x).

Определение. Математическим ожиданием M() абсолютно непрерывной случайной величины  называется величина, равная

, (2.16)

если этот несобственный интеграл сходится абсолютно. В противном случае математическое ожидание случайной величины  не существует.

Пример 2.8. Пусть случайная величина  имеет равномерный закон распределения. В этом случае плотность вероятности f(x) имеет вид

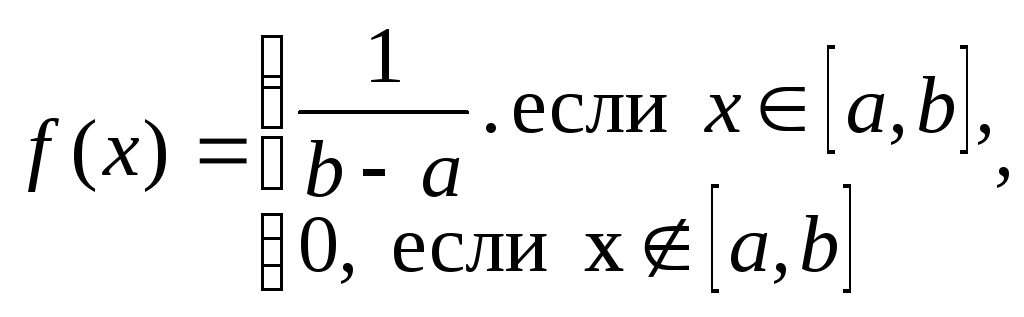. (2.17)

Тогда по формуле (2.16) получаем формулу для вычисления математического ожидания равномерно-распределенной случайной величины M()==++==.

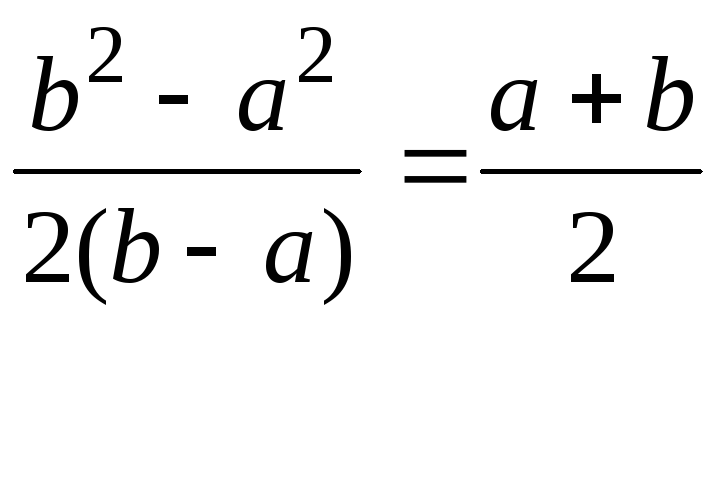Пусть  обозначает дискретную случайную величину с рядом распределения

x_i x₁ x₂ ,…, x_n,…

p_i p₁ p₂ ,…, p_n,… ,

и g(x) – некоторая функция переменной x. Новая случайная величина η = g(ξ) будет дискретной случайной величиной с рядом распределения

g(x_i)

p_i p₁ p₂ , …, p_n… ,

причем вероятности этих значений остаются теми же, что и для случайной величины , а значениями будут числа g(x_i). Тогда математическое ожидание случайной величины η = g(ξ) можно вычислить по формуле

. (2.18)

Пусть  обозначает случайную величину с плотностью вероятности f(x). Тогда математическое ожидание случайной величины η = g(ξ) можно вычислить по формуле

, (2.19)

если несобственный интеграл сходится абсолютно.

Определение. Математическое ожидание дискретной случайной величины определяется формулой

, (2.20)

если числовой ряд (2.20) сходится абсолютно.

Свойства математического ожидания

1. Если случайная величина принимает только одно значение =C, то M(C)=C.

2. При умножении случайной величины на постоянное число С математическое ожидание случайной величины  умножается на это же число, т.е. справедливо равенство M(C)=CM().

3. Свойство линейности. При сложении случайных величин математическое ожидание алгебраической суммы случайных величин равно алгебраической сумме их математических ожиданий, т.е. справедливо равенство M(+)=M()+M().

В частности, M(+C)=M()+C.

4. Мультипликативное свойство. Если случайные величины ,  независимы, то M()=M()M().