4. Блок контроля освоения дисциплины

4.1. Методические указания к выполнению контрольных работ

На втором курсе, в третьем семестре студенты выполняют контрольные работы № 5 и № 6.

Прежде чем выполнять контрольные работы, следует изучить теоретический материал по указанной литературе, разобрать решения типовых задач, приведенных в данном комплексе, выработать навыки решения примеров и задач по соответствующей теме, проверив себя по тренировочным тестам, приведенным в 4.3. При выполнении контрольных работ студентам необходимо придерживаться указанных ниже правил:

1.Контрольная работа должна быть выполнена студентом в отдельной ученической тетради в клетку, с полями не менее 3 см для замечаний преподавателя. Студенты, занимающиеся с применением ДОТ, могут выполнить работу письменно (для отправки на проверку письменные работы необходимо отсканировать) или в любом текстовом редакторе поддерживающим ввод формул (в формате .doc или .rtf).

2.На титульном листе работы указывается фамилия, имя, отчество студента, шифр (номер студенческого билета), курс, факультет и специальность, по которой студент обучается, номер контрольной работы, год издания методических указаний, из которых взято контрольное задание.

3.Условия задачи переписываются полностью, без сокращения слов, после чего приводится подробное решение со ссылками на использованные при решении определения, теоремы, формулы; в конце решения записывается ответ; чертежи можно выполнять аккуратно от руки.

4.В работу должны быть включены все задачи, указанные в задании, строго по варианту. Контрольные задания, содержащие не все задачи, а также задачи не своего варианта, не зачитываются.

5.Если в работе имеются ошибки, студент должен выполнить все требования преподавателя, изложенные в рецензии, и сдать работу с исправлениями на повторную проверку.

6.Никакие исправления в тексте уже проверенной работы не допускаются, все исправления записываются после рецензии преподавателя с указанием номера задачи, к которой относятся дополнения и исправления.

147

4.1.1. Методические указания к выполнению контрольной работы № 5

Дифференциальные уравнения первого порядка

Теоретический материал по теме изложен на с. 20-30 данного издания. Пример 1. Найти общее решение уравнения

2x(1−ey )dx +(1+ x2 )ey dy = 0.

Решение. Разделим обе части уравнения на (1+ x2 )(1−ey ), полагая, что

1−ey ≠ 0. Получим

ey

2x

dx +

dy = 0.

1+ x2

−ey

1

Выполняя интегрирование, будем иметь ln (1+ x2 )−ln |1−ey |= −ln C, где C

- произвольная положительная постоянная, или в таком виде

ln |1−ey |= ln (1+ x2 )

+ln C.

(

)

Если считать, что 1 > ey , то

или

сможем написать ey =1−C 1+ x2

y = ln (1−C (1+ x2 )). Случай 1 < ey рассматривается аналогично.

Предполагалось, что 1−ey ≠ 0.

Если 1−ey = 0 , тогда

y = 0. Эта функция

является решением уравнения, но получается из общего решения при C = 0 и

не является особым решением.

Пример 2. Найти общее решение уравнения

y

y

x − y cos

dx

+ x cos

dy = 0

x

x

для x ≥1 и его частное решение, удовлетворяющее

начальному

условию

y (1)= 0.

Решение. Переменные в этом уравнении не разделяются. Рассмотрим две

функции	λy				y
M (λx, λy)= λx −λy cos	λx	= λ x − y cos				= λM (x, y);
					x
N (λx, λy)= λx cos			λy	= λN (x, y).
			λx
Так как обе функции M (x, y) и N (x, y) - однородные первой степени, то

уравнение однородное. Чтобы получить уравнение с разделяющимися
переменными, сделаем подстановку: y = ux, где u = u (x)	- новая искомая
148

функция.

Тогда

dy

=

du

x +u

или dy = xdu +udx, и исходное

уравнение

dx

dx

принимает вид: (x −ux cosu)dx + x cosu (xdu +udx)= 0.

Упростим его, учитывая, что

x ≥1. Получим dx + x cosudu = 0.

Разделим

переменные и проинтегрируем:

∫

dx

+ ∫cos udu = 0; ln x +sin u = ln C,

где C -

x

произвольная положительная постоянная. Запишем

последнее

равенство

в виде

sin u = ln

C

. Подставляя u =

y

, получаем sin

y

= ln

C

.

x

x

x

x

Отсюда имеем общее решение:

y= x arcsin ln C .

x

Найдем теперь частное решение, удовлетворяющее заданному начальному условию. Подставим в выражение общего решения x =1 и y = 0

	и найдем значение C :
	0 = arcsin (ln C ); ln C = 0;		C =1.
	Таким образом, частное решение имеет вид: y = x arcsin				1
				ln			.
					x
								1
	Пример 3. Найти общее решение уравнения xy '+ y = e2 x						при x ≥		и его
								2
					1
	частное решение, удовлетворяющее начальному условию			y			= 3e .
					2
	Решение. Это линейное дифференциальное уравнение первого порядка,
	так как искомая функция y	и ее производная	y ' входят в него в первой
	степени. Найдем его общее	решение, считая,	что	y > 0			(случай		y < 0

рассматривается аналогично). Применим метод Лагранжа.

1) Находим общее решение соответствующего однородного уравнения: xy '+ y = 0 или x dydx + y = 0. Разделим переменные и проинтегрируем:

dy	+ dx	= 0;	ln y +ln x = ln C, y =	C	,
y	x			x

где C - произвольная положительная постоянная.

2) Общее решение неоднородного уравнения ищем в виде, определяемом

	общим решением однородного уравнения:	y =	C(x)	, где C (x) - новая
			x
	149

искомая

функция. Найдем

y ' =

C '(x)x −C (x)

и подставим y и y ' в

исходное уравнение:

x2

(x)x −C (x)

C (x)

x

C '

+

= e2 x .

x2

x

Отсюда

C '(x) = e2 x ; C (x)=

1

e2 x

+C , где C -

произвольная постоянная.

2

Получаем общее решение:

C

e2 x

y =

+

.

x

2x

	3) Для нахождения частного	решения, удовлетворяющего заданному
	начальному условию, подставляем	в выражение общего решения x =	1	и
			2
	y = 3e и находим значение C :

3e = 2C + e; 2C = 2e; C = e.

Частное решение имеет вид:

y= e + e2 x . x 2x

Дифференциальные уравнения высших порядков, допускающие понижение порядка

Теоретический материал по теме изложен на с. 32-40 данного издания.

Пример 4. Найти общее решение уравнения: y '''sin3 x −2cos x = 0.

Решение. Считая, что

sin x ≠ 0 ,

запишем

данное уравнение в виде

y ''' =

2cos x

и последовательно его проинтегрируем

sin3 x

2cos x

1

y '' = ∫

dx

= −

+C1;

sin3 x

sin2 x

1

y ' =

∫

−

+C1

dx = ctgx

+C1x +C2 ;

sin

2

x

y = ∫(ctgx +C1x +C2 )dx = ∫ cossin xx dx +C1 ∫ xdx +C2 ∫dx +C3 ,

где C1,C2 , C3 - произвольные постоянные. Общее решение имеет вид:

150

y = ln | sin x | +C

x2

+C

x +C .

2

1

2

3

Пример 5. Найти общее решение уравнения y '' =

3

y ' , считая x ≥ 0.

x +1

Решение. Это уравнение не содержит функции

y .

Его порядок можно

понизить введением новой функции

z (x)= y '.

Тогда

y '' =

dz

и уравнение

примет вид:

dx

dz

=

3

z.

x +1

dx

dz

3dx

Считая, что z > 0 , разделим переменные

=

и проинтегрируем

z

x +1

(случай z < 0 рассматривается аналогично)

ln z = 3ln(x +1) +ln C1,

где C1 - произвольная положительная постоянная. Теперь можем написать

z = C1 (x +1)3

или возвращаясь к функции y

y ' = C1 (x +1)3 .

Выполняя интегрирование, получим

y = ∫C1 (x +1)3 dx = C1 (x +41)4 +C2 ,

где C2 - произвольная постоянная.

Функция y = C (y ' = z = 0) содержится в общем решении при C1 = 0 и не

является особым решением.

Пример 6. Найти общее решение дифференциального уравнения

y '' = 2 (y ')2 ctgy .

Решение. Это уравнение не содержит аргумента x . Порядок его понижается введением новой функции p(y)= y ', зависящей явно от аргумента y . При этом

y '' = dxd (y ')= dxd (p(y (x)))= dpdy dydx = dpdy p.

Подставляя в исходное уравнение вместо y ' и y '' их выражения через функцию p(y), получим уравнение первого порядка:

151

p dpdy = 2 p2ctgy.

Разделим переменные, считая sin y ≠ 0 и p > 0 (случай p < 0 рассматривается аналогично)

	dp	=	2cos ydy	;
	p		sin y

и проинтегрируем полученное уравнение:

ln p = 2 ln | sin y | +ln C1

или в таком виде

p = C1 sin2 y ,

где C1 - произвольная положительная постоянная. Возвращаясь к искомой функции y , запишем

dydx = C1 sin2 y.

Разделив переменные, проинтегрируем это уравнение:

∫	dy		= C1 ∫dx; −ctgy = C1x +C2 ,
	sin2
		y

где C2 - произвольная постоянная.

Окончательно, общее решение исходного уравнения: y = arcctg (−C1x +C2 ).

Функция y = const (p = 0) не является особым решением уравнения, так как она содержится в его общем решении при C1 = 0.

Линейные дифференциальные уравнения

Теоретический материал по теме изложен на с. 41-57 данного издания. Пример 7. Найти общее решение уравнения y(4) +3y '' = 0 .

Решение. Выпишем характеристическое уравнение данного линейного
уравнения:	λ4 +3λ2 = 0 или λ2 (λ2 +3)= 0 . Среди его корней есть корень
λ1 = λ2 = 0	кратности k = 2 и пара комплексно-сопряженных корней

λ3 = 3i , λ4 = − 3i . Фундаментальную систему решений образуют функции

ϕ = e0 x	=1; ϕ	2	= xe0 x	= x;
1
ϕ3 = cos	3x; ϕ4 = sin			3x.

Общее решение уравнения:

y = C1 +C2 x +C3 cos 3x +C4 sin 3x,

152

где C1, C2 , C3 ,C4 - произвольные постоянные.

Пример 8. Найти общее решение уравнения y ''+ 4 y = sin 2x и его частное решение, удовлетворяющее начальным условиям y (0)= −1, y '(0)= 74 .

Решение. Решение задач такого типа целесообразно проводить по следующей схеме.

1. Находим общее решение соответствующего однородного уравнения

y ''+ 4 y = 0. Его	характеристическое	уравнение	λ2 +4 = 0	имеет корни:
λ1 = 2i,λ2 = −2i .	Фундаментальная	система	решений:	ϕ1 = cos 2x,
ϕ2 = sin 2x; общее решение однородного уравнения:
	y = C1 cos 2x +C2 sin 2x,

где C1, C2 - произвольные постоянные.

2. Ищем частное решение неоднородного уравнения по виду правой части: f (x)= sin 2x . Так как число α+iβ = 0 +2i совпадает с корнем

характеристического уравнения, то частное решение неоднородного уравнения имеет вид:

y* = x(M cos 2x + N sin 2x).

Чтобы определить неизвестные коэффициенты M и N , подставим в исходное уравнение выражения для y*, y * ', y * '' и учтем, что уравнение обратится при этом в тождество.

y * = Mx cos 2x + Nxsin 2x

(y *)' = M cos 2x −2Mxsin 2x + N sin 2x + 2Nx cos 2x

(y *)'' = −4M sin 2x −4Mx cos 2x + 4N cos 2x −4Nxsin 2x

(y *)''+4 y* = 4Mx cos 2x +4Nx sin 2x −4M sin 2x −

−4Mx cos 2x +4N cos 2x −4Nx sin 2x ≡ sin 2x.

−4M sin 2x + 4N cos 2x ≡ sin 2x

Приравниваем коэффициенты при функциях sin 2x и cos 2x , стоящих в левой и правой частях уравнения:

	−4M =1	; получаем M =	−	1	; N	= 0.
				4
	4N = 0						1
	Частное решение неоднородного уравнения:		y* = −					x cos 2x .
						4

3. Общее решение данного неоднородного уравнения:

153

y= y + y* = C1 cos 2x +C2 sin 2x − 14 x cos 2x.

4.Чтобы найти частное решение, удовлетворяющее заданным начальным условиям, вычислим производную общего решения y :

	y ' = −2C sin 2x +				2C			2	cos 2x −	1	cos 2x +		1	xsin 2x.
		1							4			2
															7
	Подставим в y и y ' начальные значения x = 0;											y (0)= −1, y '(0)=				;
															4
				−1 = C1
		7			1			откуда C1 = −1, C2 =1.
				= 2C2 −			,
		4			4

Из общего решения при C1 = −1 и C2 =1 получим искомое частное решение

y = −cos 2x +sin 2x − 14 x cos 2x

или

y = sin 2x − 14 (x + 4)cos 2x.

Пример 9. Указать вид частного решения уравнения y ''− y = 2e−x +9xe2 x .

Решение. 1. Рассмотрим соответствующее однородное уравнение: y ''− y = 0 . Его характеристическое уравнение λ2 −1 = 0 имеет вещественные

простые корни: λ1 =1, λ2 = −1.
2.	В		правой	части	уравнения	стоит сумма	двух		функций:
f (x)+ f		2	(x)= 2e−x +9xe2 x . Частное решение этого уравнения представляет
1
собой	также сумму			двух	функций (по	принципу наложения			решений):
y* = y1* + y2*. Здесь				y1* - частное решение уравнения: y2′′ − y = 2e−x ; y2* -
частное решение уравнения					y ''− y = 9xe2 x . Найдем вид		y* : f		(x)= 2e−x ;
							1	1
здесь	α = −1 совпадает с корнем характеристического уравнения λ2 = −1

первой кратности, а коэффициент при e−x равен 2, поэтому y1* = Axe−x , где А - некоторая постоянная. Теперь найдем вид y2* : f2 (x)= 9xe2 x ; здесь α = 2 не совпадает ни с одним корнем характеристического уравнения, а коэффициент при e2 x - линейная функция аргумента х, поэтому y2* = (Bx +C )e2 x , где B и C

– некоторые постоянные. Окончательно получим y* = Axe−x +(Bx +C )e2 x .

154

(x −3)n

Степенные ряды

Теоретический материал по теме изложен на с. 88-106 данного издания. Пример 10. Найти область сходимости степенного ряда

∞

n∑=1 3n n(n +1).

Решение. Составим положительный ряд из абсолютных величин членов

∞

x −3

n

Un (x)=

| x −3 |

n

исходного ряда

∑

с

общим членом

. По

3n n(n +1)

n=1 3n n(n +1)

признаку

Даламбера

полученный

ряд

сходится,

если

предел

D(x)= lim

Un+1

(x)

существует и удовлетворяет условию D(x)<1.

Un (x)

n→∞

Un+1 (x)

3n n(n +1)

D(x)= lim

= lim

| x −3 |n+1

=

Un (x)

n→∞

n→∞ 3n+1

(n +1)(n + 2) | x −3 |n

=

| x −3 |

lim

n

=

| x −3 |

lim

1

=

| x −3 |

.

+

2

2

3

n→∞ n

3

n→∞

3

| x −3 |

1

+ n

Отсюда получим

<1

или | x −3 |< 3, что равносильно −3 < x −3 < 3

3

или 0 < x < 6 . Получили интервал сходимости (0,6).

Изучим поведение ряда на концах полученного интервала. На правом конце

интервала (x = 6) получаем числовой ряд

∞

1

∑

, который сравним со

n=1 n(n +1)

∞

1

(обобщенный гармонический ряд при p = 2 ).

сходящимся рядом ∑

n=1 n2

1

lim

n(n +1)

= lim

n2

= lim

1

=1 ≠ 0,

1

1

n→∞

n→∞ n2 + n

n→∞

1

+ n

n2

∞

1

значит, по второму признаку сравнения ряд

∑

сходится. На левом

(n +

1)

(x = 0)

n=1 n

конце интервала

получаем

знакочередующийся числовой ряд

	∞	(−1)n	1
	∑			. Он сходится абсолютно, так как ряд
			n(n +1)
	n=1
				155

	∞	1
	∑		сходится.
	n=1 n(n +1)

Итак, область сходимости данного ряда: [0,6].

Для разложения функций в степенной ряд целесообразно пользоваться следующими разложениями:

∞

x

n

x

x

2

x

n

+... (−∞ < x < +∞);

1.

ex = ∑

=1 +

+

+... +

n!

n=0

1!

2!

n!

∞

2n+1

x

3

5

2n+1

2.

sin x = ∑(−1)n

x

=

−

x

+

x

−...+(−1)n

x

+... (−∞< x <+∞);

(2n+1)!

(2n+1)!

n=0

1! 3!

5!

∞

(−1)n

x

2n

x

2

x

4

−... +(−1)n

x

2n

+... (−∞ < x < ∞);

3.

cos x = ∑

=1−

+

(2n)!

n=0

(2n)!

2!

4!

∞

x

n

x

2

x

3

x

n

4.

ln (1+ x)= ∑

(−1)n+1

= x −

+

−... +(−1)n+1

+...

n

2

n

n=1

3

5.

(1+x)

α

=1+αx

+

α(α−1)

x2

+...+

α(α−1)(α−2)...(α−n+1)

xn +...

2!

n!

1

∞

(−1 < x <1).

6.

= ∑ xn =1+ x + x2 +... + xn +...

1− x

n=0

(−1 < x ≤1);

(−1 < x <1);

Ряды 1-6 сходятся при указанных в скобках условиях.

Пример 11. Разложить в ряд по степеням x функцию

f (x)=

24

.

16 + x2

Решение. Преобразуем искомую функцию:

24

=

24

=

24

1

=

3

1

=

3

1

.

16 + x2

x

2

16

1 +

x2

2

+

x2

2

x

2

1

16

1

+

1−

−

16

16

16

16

1

∞

x

2

В разложении

= ∑ xn

заменим переменную x выражением

−

,

1− x

n=0

16

1

1

∞

(−1)n

x

2 n

∞

(−1)n

x

2 n

=

=

∑

= ∑

.

1 +

x 2

1 − −

x 2

n =0

16 n

n =0

2 4 n

16

16

Этотрядсходитсяабсолютнопри

x2

<1, тоестьпри

x

< 4 . Окончательно имеем:

16

2n

2n

24

3

∞

x

∞

x

(

)

=

∑

(−1)n

= 3 ∑ (−1)n

,

x

< 4

.

16 + x2

24n+1

2 n=0

24n

n=0

156

Пример 12. Разложить по степеням x функцию cos2 2x . Решение. Используя формулу

cos2 α =

1

(1+cos 2α),

2

запишем данную функцию в виде

cos2 2x =

1

(1+cos 4x)=

1

+

1

cos 4x.

2

2

2

∞

x

2n

Применяя разложение для cos x = ∑ (−1)n

и заменяя аргумент x на

(2n)!

4x , запишем

n=0

∞

4

2n

x

2n

∞

2

4n

x

2n

cos 4x = ∑ (−1)n

= ∑

(

−1)n

(2n)!

n=0

(2n)!

n=0

1

1

∞

n

2

4n

x

2n

1

∞

2

4n

x

2n

cos2 2x =

+

1

+ ∑

(−1)

=1

+

∑

(−1)n

=

(2n)!

2 2

n=1

(2n)!

2 n=1

∞

2

4n−1

x

2n

(

)

=1+ ∑(−1)n

,

x

< ∞

.

(2n)!

n=1

4.1.2. Методические указания к выполнению контрольной работы № 6

Двойные интегралы

Теоретический материал по теме изложен на с. 107-121 данного издания.

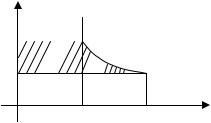
Пример 13. Изменить порядок интегрирования в двойном интеграле

2

4 / y

∫dy ∫ f (x, y)dx.

1

0

Сделать чертеж области интегрирования.

y

D

y

x = 2

Решение.

Переменная

в

области

4

изменяется в

промежутке:

1 ≤ y ≤ 2, то

есть

2

x =

область D заключена между горизонтальными

D1

y

1

D2

прямыми:

y =1

и

y = 2 .

Пределы

x

интегрирования по переменной

x

показывают,

O

2

4

что слева область D ограничена линией x = 0,

то есть осью

Oy , а справа – линией x = 4 / y ,

Рис. 1

157

которая является гиперболой. На рис. 1 область D заштрихована. Теперь поменяем порядок интегрирования, приняв за внешнюю переменную не y , а

x . Поскольку верхняя граница области D состоит из двух участков, заданных

по-разному: y = 2

при

0 ≤ x ≤ 2 и

x = 4 / y

при

2 ≤ x ≤ 4,

то

разобьем

область D вертикальной прямой x = 2 на области D1 и D2 . Тогда

∫∫ f (x, y)dxdy =∫∫

f (x, y)dxdy + ∫∫

f (x, y)dxdy =

D

D1

D2

2

2

(x, y)dy +

4

4 / x

= ∫dx∫ f

∫dx ∫ f (x, y)dy.

y

0

1

2

1

A

4

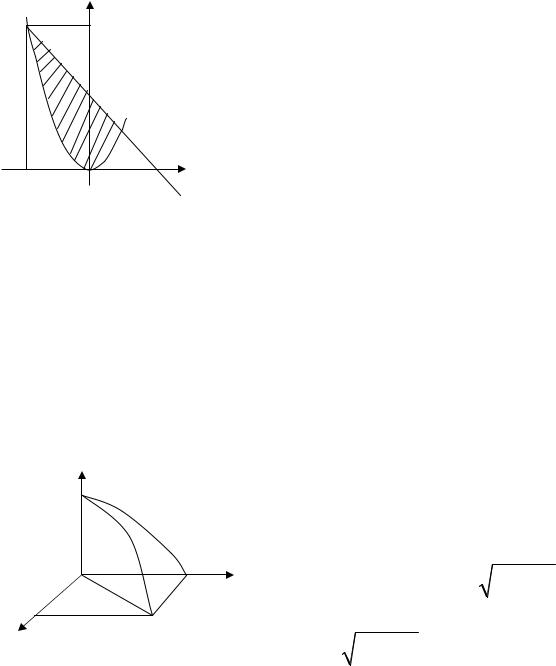
Пример

14.

Найти

массу

пластины,

y

= 2

− x

ограниченной

линиями:

y = x2

и

y = 2 − x,

имеющей плотность μ(x, y)= y .

1

B

Решение. Область интегрирования D ограничена

снизу параболой y = x2 ,

а сверху прямой

y = 2 − x

y = x2

x

O

(рис. 2). Точки пересечения этих линий

A(−2, 4) и

−2

1

B(1,1). Переменная

x

изменяется

в

пределах

Рис. 2

−2 ≤ x ≤1. Получим:

1

2−x

M = ∫∫μ(x, y)dxdy = ∫∫ ydxdy = ∫ dx ∫

ydy.

D

D

−2

x2

Вычислим сначала внутренний интеграл, считая x фиксированной

величиной, а затем - внешний интеграл

1

1

y

2

2−x

1

1

1

3

5

M =

∫

dx =

∫

(

(x −

2)2 − x4

dx =

(x−2)

−

x

= 7, 2.

2

−2

2

2

−2

)

2

3

5

x

−2

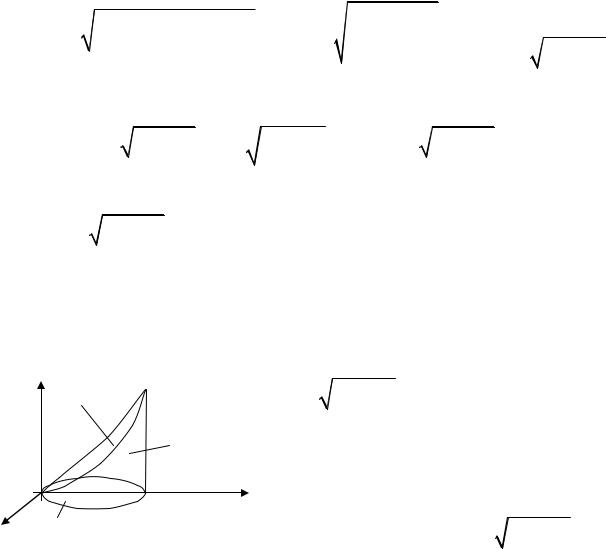
Пример 15.

Найти площадь части поверхности

σ кругового

цилиндра

4

z

y2 + z2 =16 ,

вырезанной

плоскостями

y = x, x = 0, z = 0,

лежащей в первом октанте

(рис. 3).

O

σ

B

y

Решение.

Из

уравнения

кругового

цилиндра выразим

z : z =

16 − y2 .

Найдем

x 4

4

Рис. 3

A

частные производные этой функции:

fz′ = 0

f y′ = −y / 16 − y2 .

Площадь S рассматриваемой поверхности σ будем вычислять по формуле:

158

Тогда для области

Sσ = ∫∫		1+( f 'x )2 +(f 'y )2 dxdy = ∫∫											1+				y2		dxdy = 4∫∫						dxdy	=
																	− y2
D											D		16							D			16 − y2
= 4∫dy∫			dx				= 4 ∫		1				x		y				y	dy =
															dy = 4∫
	4	y					4										4
	0	0 16 − y2					0		16−y2						0		0 16 − y2
4	d(16 − y			2	)		4		− y2 )−	1										1					4
= −4∫						= −2∫(16				2	d (16 − y2 ) =− 4 (16 − y2 )											2			=16.
0	2	16 − y2					0																		0

x2

x

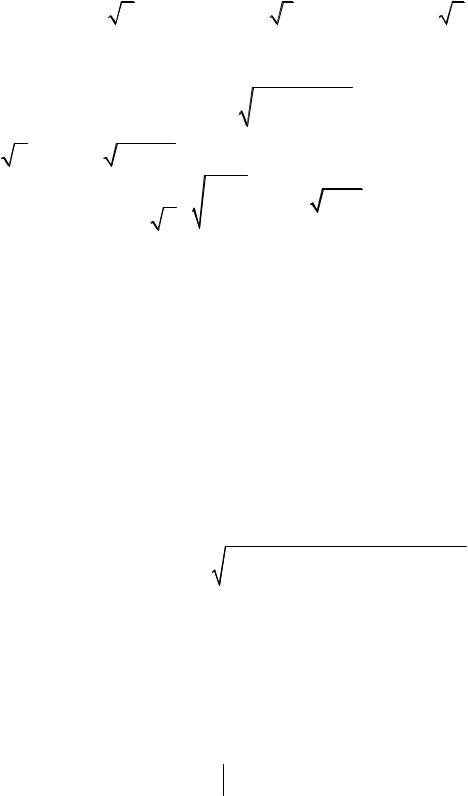
Пример 16. Найти объем тела T , заданного неравенствами:

+ y2 ≤ 2 y, z2 ≤ x2 + y2 , z ≥ 0.

Решение. Данное тело изображено на рис. 4. Оно ограничено цилиндром

z z2 = x2 + y2			x2 + y2 = 2 y ,	частью		конуса
			z = x2 + y2	и координатной плоскостью
		x2 + y2 = 2 y	Oxy . Проекцией D данного тела на
			плоскость Oxy является круг радиусом 1 с
O		y	центром, расположенным		на	оси Oy в
	1	2	точке y =1.
	D Рис. 4		V = ∫∫z (x, y)dxdy = ∫∫		x2 + y2 dxdy.
			D	D

Перейдем к полярным координатам. Учитывая, что x2 + y2 = r2 , запишем

уравнение окружности, ограничивающей область D в полярных координатах: x2 + y2 = 2 y r2 = 2r sin ϕ r = 2 sin ϕ. D : 0 ≤ ϕ ≤ π,

0 ≤ r ≤ 2 sin ϕ. Следовательно, учитывая, что Якобиан равен r , будем иметь

V = ∫∫z (r cos ϕ, r sin ϕ)rdϕdr = ∫∫r2dϕdr =

				D										2 sin ϕ		D
		π		2 sin ϕ			1		π							8	π
	= ∫dϕ			∫	r2dr =				∫ dϕr3						=		∫sin3	ϕd	ϕ =
							3									3
		0		0					0					0			0			π
	8	π			2					8							cos3 ϕ				32
= −		1	−cos			ϕ d cos			ϕ = −			cos ϕ−					3			=		.
	3									3											9
		0∫(				)
																				0

159

Криволинейные интегралы

Теоретическийматериалпотемеизложеннас. 122-138 данногоиздания.

Пример 17. Вычислить криволинейный интеграл первого рода ∫8x + y2 dl ,

L y

где L - дуга параболы y = 2 x от точки A(3, 2 3 ) до точки B(8, 4 2 ). Решение. Для вычисления криволинейного интеграла первого рода

используем формулу

∫ f (x, y)dl = b∫ f (x, y (x))

1+(y '(x))2 dx.

L

a

Так как y ' =1/ x , то dl =

1 +1/ x dx .

8x + y2

8

8x + 4x x +1

8

∫

dl = ∫

dx = 6∫ 1+ xdx =

y

2

x

x

L

(1 x)

3

)

3

2

3/ 2

8 = 4

(

= 6

+

93/ 2 −43 / 2

= 76.

3

Пример

18.

3

Вычислить

криволинейный

интеграл

второго рода

∫(2 − y)dx + xdy по кривой L : x = t −sin t; y =1−cost от точки A с tA = 2π

L

до точки B с tB = 0.

Решение.

Если плоская кривая L задана явно y = y (x);

a ≤ x ≤b , то

∫P(x, y)dx +Q(x, y)dy = b∫(P(x, y (x))+Q(x, y(x))y '(x))dx.

L

a

y = y (t ); z = z (t ),

Если кривая L задана параметрически x = x(t );

t1 ≤ t ≤ t2 , то для вычислений используется формула:

∫ f (x, y, z)dl =t∫2 f (x(t ), y(t ), z (t )) (x '(t ))2 +(y '(t ))2 +(z '(t ))2 dt.

L		t1
Для данной кривой dx = (1−cost )dt; dy = sin tdt ,тогда
∫	(2 − y)dx + xdy =		0	(	(1+cos t )(1−cos t )+(t −sin t )sin t dt =
			∫						)
L		u = t,	2π		du = dt
=	0					=(−t cost )		0	0
	∫	t sin tdt =							+ ∫ cos tdt =
	2π	dv = sin t, v = −cos t						2π	2π

= 2π+(sin t )02π = 2π.

160