3.2. Опорный конспект лекций по дисциплине

Введение

В предлагаемом Вам опорном конспекте лекций по курсу математики в краткой и сжатой форме изложен теоретический материал, широко проиллюстрированный решенными примерами, необходимый к усвоению в течение третьего семестра на втором курсе обучения в СЗТУ. В каждом разделе конспекта указаны количество и номера задач, которые необходимо решить для осуществления текущего и итогового контроля.

Раздел 1. Обыкновенные дифференциальные уравнения

Данный раздел включает темы:

1.1.Основные понятия.

1.2.Основные типы уравнений первого порядка .

По каждой теме излагается основной теоретический материал и приводятся иллюстрирующие примеры. В рубрике “Решение задач” дан подробный разбор типовых примеров.

Студентам очно-заочной и заочной форм обучения надо решить одну задачу из контрольной работы № 5.

1.1.Основные понятия

Врассматриваемой теме Вам предстоит познакомиться со следующими вопросами:

•Порядок и решение дифференциального уравнения. Интегральная кривая;

•Задача Коши. Общее и частное решения.

После изучения теоретического материала следует ответить на вопросы для самопроверки и на вопросы теста №1. При возникающих затруднениях в ответах обратитесь к [1].

Порядок и решение дифференциального уравнения. Интегральная кривая

Уравнения, в которых содержатся производные неизвестных функций,

называются дифференциальными уравнениями.

Неизвестные функции, входящие в уравнения, могут зависеть от одной или нескольких независимых переменных: в первом случае они называются

обыкновенными дифференциальными уравнениями, во втором случае -

Данный подраздел имеет собственную нумерацию рубрик.

15

дифференциальными уравнениями в частных производных. Мы будем рассматривать только обыкновенные дифференциальные уравнения.

Порядок старшей производной, входящей в дифференциальное уравнение,

называется порядком этого уравнения.

Так, например, уравнения

y '+ xy2 = sin x, xy '3 + ex = 5, ln( y '2 + x2 ) − xtgy = ayx

являются обыкновенными дифференциальными уравнениями первого порядка,

а	уравнения	xy ''− y '3 + 2xy = 0,			y ''+ 5 y '+ 6 y = 2x		-	обыкновенными
дифференциальными уравнениями второго порядка.
	Любое обыкновенное дифференциальное уравнение n -го порядка с одной
неизвестной функцией y аргумента x всегда можно записать в виде
			F (x, y, y '',..., y(n) ) = 0,							(1.1)
где	F - известная		функция своих аргументов, причем					производная		y(n)
обязательно содержится в уравнении.										X
	Решением дифференциального уравнения (1.1) на							промежутке
называется функция			y = ϕ(x) , n раз дифференцируемая на этом промежутке,
при подстановке		которой вместо		y	в уравнение	(1.1),	оно обращается в
тождество на всем промежутке X , т.е.
		F (x,ϕ(x),ϕ'(x),ϕ''(x),...,ϕ(n) (x)) ≡ 0,				x X .
Например, функция			y = x2 является решением уравнения				xy '− 2 y = 0 на всей
числовой оси.			y = ϕ(x) дифференциального уравнения (1.1)
	График решения								называется
интегральной кривой этого уравнения.									Φ(x, y) = 0 ,
	Заметим, что	иногда решение		получают в неявной			форме

называя его интегралом дифференциального уравнения, или в параметрическом виде x = x(t), y = y(t), где t - параметр.

Процесс отыскания решений дифференциального уравнения называется

интегрированием этого уравнения.

Одной из задач теории дифференциальных уравнений является интегрирование уравнений в квадратурах (в конечном виде), т.е. в получении замкнутой формулы, дающей (в явной, неявной или параметрической форме) выражение зависимости того или иного решения от аргумента, через заданные функции и интегралы от них. Квадратурой называется операция взятия неопределенного интеграла.

Отметим специально, что в теории дифференциальных уравнений под символом ∫ f (x)dx понимают какую-нибудь одну первообразную, а

постоянную интегрирования пишут отдельно. Дифференциальное уравнение первого порядка имеет вид

F (x, y, y ') = 0,	(1.2)
16

Уравнение (1.3) всегда можно записать в виде

где x - независимая переменная, y - его неизвестная функция, a F - заданная функция своих переменных в некоторой области пространства трех переменных. Если это уравнение может быть разрешено относительно производной y ' , то получим уравнение вида

y ' = f (x, y),	(1.3)
где f (x, y) - известная функция, определенная в некоторой области	D на

плоскости Oxy . Уравнение вида (1.3) называют уравнением, разрешенным

относительно производной или уравнением в нормальной форме.

f (x, y)dx − dy = 0, которое является частным случаем уравнения вида P(x, y)dx − Q(x, y)dy = 0.

Последнее уравнение примечательно тем, что x и y равноправны, так как из самого уравнения не следует, какая из переменных является независимой, а какая - функцией.

Задача Коши . Общее и частное решения

При решении многих задач требуется найти не все решения уравнения (1.3), а только такое, которое принимает заданное значение при заданном значении

независимой переменной, а именно, требуется найти		решение y(x),
удовлетворяющее условию
	y(x0 ) = y0 ,	(1.4)
где x0	и y0 любые числа, для которых определена функция	f (x, y). Условие
(1.4)	называют начальным условием, числа x0 и y0	- начальными

значениями решения уравнения (1.3), а саму задачу - задачей Коши или начальной задачей. С геометрической точки зрения задача Коши состоит в

нахождении интегральной кривой, проходящей через данную точку M (x0 , y0 ).

На вопрос о существовании и единственности решения задачи Коши отвечает следующая теорема, которую мы приводим без доказательства и в

упрощенной формулировке.	y ' = f (x, y)	функция f (x, y) и ее частная
Теорема 1.1. Если в уравнении
производная ∂∂fy непрерывны в некоторой области			D на плоскости Oxy , то
какова бы ни была точка (x0 , y0 )	области	D ,	существует единственное
решение y = ϕ(x) уравнения (1.3),	определенное		в некотором интервале,

содержащем точку x0 и удовлетворяющее условию ϕ(x0 ) = y0.

В частности, если два решения ϕ1(x) и ϕ2 (x) уравнения (1.3) совпадают

хотя бы для одного значения x , то эти решения тождественно равны для всех тех значений x , для которых они оба определены.

Огюстен Коши (1789-1857)-французский математик.

17

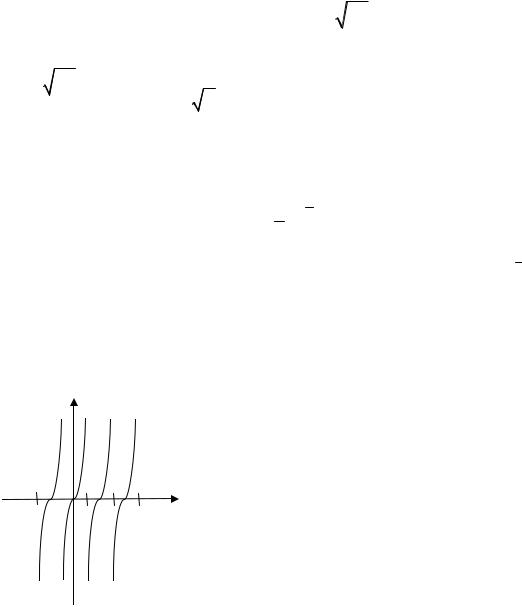
Геометрический смысл этой теоремы состоит в том, что через каждую точку (x0 , y0 ) области D проходит одна и только одна интегральная кривая

уравнения (1.3) или, другими словами, вся область D покрыта интегральными кривыми уравнения (1.3), которые нигде не пересекаются между собой.

			Общее, частное и особое решения. Если
y		yn	закрепить начальное значение абсциссы			x0 , а
			начальному значению y		придавать различные
		y3	допустимые	значения	y1 , y2 , y3 ,..., yn , то
		y2
		y1	каждому	такому	значению	будет
			соответствовать единственная интегральная
0		x
			кривая (рис. 1.1) и, следовательно, в области
		x0
			D множество всех интегральных кривых
	Рис. 1.1
			образует семейство кривых, зависящих от
			одного параметра, который может изменяться

в определенных пределах и который принято обозначать через C , так что все семейство интегральных кривых может быть описано уравнением y = ϕ(x,C).

Определение. Функция
y = ϕ(x,C)	(1.5)

непрерывно дифференцируемая по x называется общим решением уравнения (1.3) в области D , если она удовлетворяет следующим двум условиям:

1) равенство (1.5) разрешимо в области D	относительно произвольной
постоянной C
C = Ψ(x, y),	(1.6)

2) функция ϕ(x,C) является решением уравнения (1.3) для всякого значения постоянной C , полученной из формулы (1.6), в которой точка (x, y) - любая точка из области D .

Естественно, что знание общего решения (1.5) дает возможность решить

задачу Коши для любых начальных значений				x0 , y0 из области D . Для этого
достаточно заменить в формуле (1.5)			переменные x и y		числами	x0 и y0 ,
решить полученное уравнение		y0 = ϕ(x0 ,C)		относительно	C , т.е.	получить
соотношение	C = Ψ(x0 , y0 )	и подставить		найденное значение		в общее
решение (1.5).	Полученная функция		y = ϕ(x, Ψ(x0 , y0 ))		и есть	искомое

решение. Общее решение уравнения (1.3), записанное в виде, не разрешенном относительно искомой функции, т.е. в виде

Φ(x, y, C) = 0 или Φ(x, y) = C ,

называют общим интегралом этого уравнения.

Решение, которое получается из общего решения y = ϕ(x,C), если в последнем произвольной постоянной C придать конкретное (допустимое) значение, называется частным решением. Аналогично определяются частные интегралы.

18

Решение, которое не может быть получено из общего решения (общего интеграла) ни при каком конкретном значении произвольной постоянной, называется особым решением. Геометрически особому решению соответствует интегральная кривая, не содержащаяся в семействе интегральных кривых, составляющих общее решение (общий интеграл). Особое решение примечательно тем, что через каждую точку изображающей его интегральной кривой проходит, по крайней мере, еще одна интегральная кривая того же

уравнения, имеющая в этой точке ту же касательную.

D условиям

Если правая часть уравнения (1.3) удовлетворяет в области

теоремы 1.1, то это уравнение не имеет в области D особых решений.

Пример 1.1. Рассмотрим уравнение

y ' = 33 y2 .

(1.7)

Так

как правая

часть

уравнения (1.7)

и ее

частная

производная

∂

2

−

1

2

(33

y2 ) = 3 3

y

3

=

удовлетворяют условиям

теоремы

1.1 во всех

∂y

3 y

точках плоскости Oxy

за исключением точек оси Ox ,

то через любую точку

(x0 , y0 ) при y0

≠ 0

проходит единственная

интегральная кривая уравнения

(1.7). Для отыскания общего решения запишем уравнение (1.7) в виде

1 −2 =

3 y 3 dy dx.

1

В левой части равенства стоит дифференциал функции y3 , а в правой - дифференциал функции x . Из равенства дифференциалов этих функций следует, что сами эти функции могут отличаться лишь на произвольное

1

постоянное слагаемое C , так что можем написать

y

3

= x + C

или в таком

виде

y = (x +C)3 .

y

(1.8)

Функция (1.8) является общим решением уравнения

(1.7) всюду на плоскости Oxy за исключением оси Ox .

0

x

Непосредственно видно,

что, подставив функцию

-3

1

3 5

y = 0 в уравнение (1.7), получим тождество, т.е. y = 0

является решением данного уравнения, притом особым

3

3

3

3

решением,

так как оно не может быть получено из

y=(x+2)

y=x

y=(x2)-

y=(x-4)

общего решения

y = (x +C)3 ни при каком значении

постоянной

C .

Заметим, что через каждую точку

Рис. 1.2

M

0

(x , 0)

оси

Ox

проходит кривая

y = (x − x )3

,

0

0

совпадающая при y0

≠ 0 с общим решением (1.8)

и

касательной к которой в этой точке является сама ось Ox (рис. 1.2).

19

В дальнейшем слова решить (проинтегрировать) дифференциальное уравнение будут означать одно из двух:

а) найти его общее решение (общий интеграл), если начальные условия не заданы;

б) найти частное решение (частный интеграл), удовлетворяющее заданным начальным условиям.

Далее будут рассмотрены типы дифференциальных уравнений первого порядка, интегрируемых в квадратурах, и указаны пути получения общего решения (общего интеграла).

Вопросы для самопроверки по теме 1.1

1.Какие уравнения называются дифференциальными?

2.Какие дифференциальные уравнения называются обыкновенными?

3.Как определить порядок дифференциального уравнения?

4.Какая функция называется решением дифференциального уравнения?

5.Интегральной кривой дифференциального уравнения называется ….... (закончить фразу).

6.Сформулируйте задачу Коши для дифференциального уравнения первого порядка.

7.Дайте определения общего и частного решений дифференциального уравнения первого порядка.

1.2.Основные типы уравнений первого порядка

Врассматриваемой теме Вам предстоит познакомиться со следующими вопросами:

•Уравнения с разделяющимися переменными;

•Однородные уравнения первого порядка;

•Линейные уравнения первого порядка.

После изучения теоретического материала следует ответить на вопросы самопроверки и на вопросы теста №2. При возникающих затруднениях в ответах обратитесь к [1].

Студентам очно-заочной и заочной форм обучения надо решить одну задачу из контрольной работы № 5 под номерами 1-10 в соответствии со своим вариантом.

Уравнения с разделяющимися переменными

Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если его можно записать в виде

y ' = f (x) g( y) ,

(1.9)

20

где функции f (x) и g( y) непрерывны соответственно на интервалах

x (a, b), y (c, d ), а функция g( y)				имеет непрерывную	производную на
(c, d ).
Если уравнение (1.9) умножить на		dx		(при g( y) ≠ 0 ), то получим уравнение
		g( y)
	dy		= f (x)dx		(1.10)
	g( y)

уже с разделенными переменными. Если в уравнении (1.10) под y понимать решение уравнения (1.9), то равенство (1.10) означает равенство дифференциалов (в правой части этот дифференциал выражен непосредственно через независимую переменную x , а в левой части – через посредство y , являющегося функцией x ). Из равенства дифференциалов следует, что их неопределенные интегралы могут различаться только на произвольное постоянное слагаемое C , так что можем написать

∫	dy	= ∫ f (x)dx +C .	(1.11)
	g( y)
Соотношение (1.11) представляет собой общий интеграл уравнения (1.9) в
прямоугольнике
(a < x < b, c < y < d ).			(1.12)
Пример 1.2. Найти решение уравнения
y ' = x4 (1+ y2 ) ,			(1.13)
удовлетворяющее начальному условию y(0) =1.

Данное уравнение есть уравнение с разделяющимися переменными,

записанное в	виде (1.9) (здесь f (x) = x4 , а g( y) =1+ y2 ). Функции x4 и
(1+ y2 ) 'y = 2 y	непрерывны при любых значениях x и y , причем 1+ y2 ≠ 0.
Умножив обе части данного уравнения на dx и разделив на 1+ y2 , имеем
		dy	= x4dx.
	1+ y2

В согласии с равенством (1.11) получим общий интеграл данного уравнения на всей плоскости Oxy в виде

			∫1+ y2			∫
				dy	=		x4dx +C .	(1.14)
	Выполняя операции интегрирования, получим
	arctgy =	x5	+ C, где C - произвольная постоянная.					(1.15)
		5

Для решения поставленной задачи Коши положим в полученном общем

интеграле x = 0, y =1. Будем иметь	arctg1 = C , т.е. C =	π	. Подставив найденное
		4
	21

значение C в равенство (1.15) и разрешив относительно y , получим частное решение, удовлетворяющее заданному начальному условию

	x5			π
	y = tg		+		.
		5		4

Однородные уравнения первого порядка

Рассмотрим еще один тип дифференциальных уравнений первого порядка, интегрируемых в квадратурах. Прежде чем дать определение этого типа уравнений, приведем понятие об однородной функции.

Определение. Функция Φ(x, y) называется однородной функцией степени m относительно переменных x и y , если умножение каждого из ее аргументов

наодноитожепроизвольноечисло λ > 0 равносильноумножениюеена λm , аименно

Φ(λx,λy) = λmΦ(x, y), где m - действительное число.

(1.16)

Например,

функция

Φ(x, y) = x3 +2xy2

является

однородной

функцией

третьей степени относительно x и y , ибо

Φ(λx,λy) = (λx)3 + 2λx(λy)2 = λ3 x3 + 2λ3xy2 = λ3 (x3 + 2xy2 ) = λ3Φ(x, y).

x2 −3xy

x3

x

Аналогично, функции

f (x, y) =

,

ϕ(x, y) =

+ y2 ln

являются

x2

+ y2

y

y

однородными функциями соответственно нулевой и второй степени.

Функции x3 −2xy + y,

ex−y +2 однородными не являются,

так как для них

условие (1.16) не выполняется ни при каких m .

Дифференциальное уравнение

y ' = f (x, y)

(1.17)

f (x, y) есть

называется однородным, если его правая часть

однородная

функция нулевой степени относительно своих аргументов.

Сделаем подстановку

y(x) = xu(x),

(1.18)

где u(x) - новая неизвестная функция и вычислим

y ' = u + xu ' .

(1.19)

Подставив (1.18) и (1.19) в уравнение (1.17), получим

u + xu′ = f (x, xu), но так

как f (x, y) -

однородная функция

нулевой

степени, то

сможем

написать

u + xu′ = f (1, u)

или считая, что x ≠ 0

u′ =

f (1,u) −u

, а

это

уравнение с

x

разделяющимися переменными, в котором u = u(x) - неизвестная функция.

Пример 1.3. Решить уравнение при x ≥1:

y ' =

y

ln

y

+1 .

(1.20)

x

x

22

f (x, y) =

y

ln

y

+1

x

≥

1, y

>

0

,

Функция

определена в области {

так как

x

x

ln

y

имеет смысл лишь при

y

> 0 .

Данное уравнение является однородным,

x

x

y

y

так

как функция

ln

+1

-

однородная функция

нулевой

степени

x

x

относительно своих аргументов в указанной области, ибо

f (λx,λy) =	λy	λy			y		y		= f (x, y).
	ln		+1	=		ln		+1
		λx					x
	λx				x

Введем подстановку y = xu(x) ,		где u			- новая неизвестная функция. При этом
y ' = u + xu ' . Осуществив подстановку, получим								u + xu ' = u(ln u +1), откуда
следует уравнение с разделяющимися переменными
Решая его в области {			xu ' = u ln u.						(1.21)
	x ≥1, u > 0
			}, будем иметь
			du		=	dx	(u ≠1)
или, выполняя интегрирование			u ln u			x
	ln | ln u |= ln x +ln C,
где произвольная постоянная записана в							виде ln C при		условии C > 0. Из
последнего равенства следует			| ln u |= Cx.
									(1.22)
Очевидно, что если u >1 , то ln u = Cx ,							если же u <1, то ln u = −Cx , а тогда,
считая, что произвольная постоянная					C может принимать и отрицательные
значения, сможем записать равенство (1.22) в виде								ln u = Cx	или
			u = eCx .						(1.23)

При разделении переменных считалось, что u ≠1. Непосредственно видно, что u =1 является решением уравнения (1.21) и что оно не потеряно, а содержится в семействе (1.23) при C = 0 . Возвращаясь к старой переменной,

получим y = xeCx - общее решение уравнения (1.20) в области {x ≥1, y > 0}, где

C - любое число.

Заметим, что если P(x, y) и Q(x, y) - однородные функции одной и той же степени, которые непрерывны в некоторой области D и не обращаются одновременно в нуль ни в одной точке этой области, то дифференциальное уравнение

P(x, y)dx +Q(x, y)dy = 0

(1.24)

также является однородным и с помощью подстановки (1.18) приводится к уравнению с разделяющимися переменными.

23

Линейные уравнения первого порядка

Рассмотрим третий тип дифференциальных уравнений первого порядка интегрируемых в квадратурах.

Определение. Дифференциальное уравнение первого порядка называется линейным, если оно может быть записано в виде

y '+ p(x) y = q(x),

(1.25)

где y(x) -искомая функция аргумента x , а p(x) и q(x) - заданные непрерывные функции на промежутке X . Отметим специально, что данное уравнение линейно относительно искомой функции y и ее производной y ' .

Легко видеть, что в согласии с теоремой 1.1 уравнение (1.25) имеет единственное решение y = y(x) , удовлетворяющее условию y(x0 ) = y0 , где начальное значение y0 можно выбирать произвольным, а значение x0 брать

любым из промежутка X .

Если q(x) = 0 всюду в X , то уравнение (1.25) называют линейным однородным уравнением или линейным уравнением без правой части. В противном случае его называют линейным неоднородным уравнением или линейным уравнением с правой частью.

В частности, однородное линейное уравнение имеет решение y(x) ≡ 0 ,

называемое нулевым или тривиальным.

Существует несколько методов решения линейных дифференциальных уравнений. Остановимся на двух из них.

Метод вариации произвольной постоянной (метод Лагранжа).

Рассмотрим вначале однородное уравнение
y '+ p(x) y = 0.	(1.26)

Заметим, что так как уравнение (1.26) имеет нулевое решение y(x) ≡ 0 в X , то ни одно решение этого уравнения не может обратиться в нуль ни в одной точке промежутка X , ибо в этой точке нарушилась бы теорема 1.1. Это означает, что любое решение уравнения (1.26) не меняет знака, т.е. график решения лежит либо выше оси Ox , либо ниже оси Ox .

Рассмотрим случай, когда y(x) > 0 . Легко видеть, что уравнение (1.26) является уравнением с разделяющимися переменными. Разделяя переменные,

можем написать y ' = −p(x) y или				dy	= −p(x)dx .	Интегрируя,	получим
				y
ln y = −∫ p(x)dx +ln C,		где C	-	произвольная		положительная	постоянная.
После потенцирования найдем
				y = Ce−∫p( x)dx .			(1.27)
Для случая	y(x) < 0	получим аналогичное выражение, у которого C < 0 .
Если заметить,	что при C = 0		выражение (1.27)			дает решение	y(x) ≡ 0 , то

можно утверждать, что равенство (1.27) представляет собою общее решение

24

однородного уравнения (1.26) в полосе {x X , −∞ < y < +∞}, если считать C

произвольной постоянной.

Перейдем теперь к решению неоднородного уравнения (1.25). В согласии с методом Лагранжа будем искать его решение в виде формулы (1.27), заменяя в ней произвольную постоянную C некоторой, пока неизвестной и непрерывно

дифференцируемой на X функцией C(x) , т.е.
y = C(x)e−∫p( x)dx ,	(1.28)

где функцию C(x) нужно выбрать так, чтобы функция (1.28) была решением уравнения (1.25) (варьируем произвольную постоянную). Подставляя (1.28) в уравнение (1.25), имеем

C '(x)e−∫p( x)dx +C(x)e−∫p( x)dx (−p(x)) + p(x)C(x)e−∫p( x)dx = q(x), откуда

	C '(x)e−∫p( x)dx = q(x)		или C '(x) = q(x)e∫p( x)dx .
Выполняя интегрирование, будем иметь
где C		C(x) = ∫q(x)e∫p( x)dxdx +C,								(1.29)
	- произвольная постоянная.			Подставив				(1.29) в	(1.28),	получим
выражение
	y = e	−∫p( x)dx		∫q(x)e	∫p( x)dx					(1.30)
							dx +C ,
которое	представляет собою общее			решение		уравнения			(1.25)	в полосе
{x X , −∞ < y < +∞}.

Метод И.Бернулли. В согласии с этим методом будем искать решение уравнения (1.25) в виде произведения двух непрерывно дифференцируемых на промежутке X функций u(x) и v(x) , одна из которых может быть выбрана по нашему желанию, а другая определяется с помощью уравнения (1.25), так что

y(x) = u(x) v(x).	(1.31)
Подставив (1.31) в уравнение (1.25), получим (опуская аргумент x)
u ' v +uv '+ puv = q
или в таком виде:
v(u '+ pu) +uv ' = q.	(1.32)

Реализуем теперь свое право выбора функции u(x) , взяв в качестве ее такую, чтобы коэффициент при v (т.е. выражение, стоящее в круглых скобках)

равнялся нулю
u '+ pu = 0.	(1.33)

Для этого в качестве u(x) надо взять любое ненулевое решение уравнения (1.33). Уравнение вида (1.33) было решено выше и его общее решение имеет вид (1.27). Для получения искомого решения проще всего взять C =1, и тогда получим

25

u(x) = e−∫p( x)dx .

(1.34)

Подставив (1.34) в уравнение (1.32), имеем уравнение для определения функции v(x) :

v '(x)e−∫p( x)dx = q(x) , откуда v '(x) = q(x)e∫p( x)dx .
Выполняя интегрирование, сможем записать
v(x) = ∫q(x)e∫p( x)dxdx +C,	(1.35)
где C - произвольная постоянная. Подставив (1.34) и (1.35) в (1.31), получим
общее решение уравнения (1.25) в виде (1.30).
Пример 1.4. Решить уравнение
y '−2xy = 4x3ex2	(1.36)

для x ≥1 двумя методами: Лагранжа и Бернулли.

1. В согласии с методом Лагранжа рассмотрим сначала однородное

	уравнение
	y '−2xy = 0.		dy	(1.37)
	Разделяя переменные, можем написать y ' = 2xy	или		= 2xdx,( y ≠ 0) .
			y
	Выполняя интегрирование, получим общее решение уравнения (1.37)
	y = Cex2 ,			(1.38)

где C - произвольная постоянная. По методу Лагранжа будем искать решение неоднородного уравнения (1.36) в виде (1.38), но вместо произвольной постоянной C возьмем некоторую непрерывно дифференцируемую функцию C(x) , так что решение получим в виде

			y = C(x)ex2 .				(1.39)
Подставив	(1.39)	в	уравнение	(1.36),	сможем		написать
C '(x)ex2 +C(x)ex2 2x −2xC(x)ex2 = 4x3ex2 , откуда следует						C '(x) = 4x3.
Интегрируя, найдем			C(x) = x4 +C,
							(1.40)
где C - произвольная постоянная. Подставив (1.40)					в (1.39),	получим общее

решение уравнения (1.36) на плоскости Oxy в виде y = (x4 +C)ex2 .

2. Следуя методу И.Бернулли, будем искать решение уравнения (1.36) в

виде
y(x) = u(x) v(x),	(1.41)

где u(x) и v(x) - непрерывно дифференцируемые функции, одна из которых может быть выбрана произвольно. Подставив (1.41) в (1.36), получим

26

u 'v +uv '−2xuv = 4x3ex2	или	v(u '−2xu) +uv ' = 4x3ex2 .	(1.42)
Выберем функцию u(x) так,	чтобы	коэффициент при v	равнялся
тождественно нулю, т.е.
u '−2xu = 0.			(1.43)

Решая уравнение (1.43) точно так же, как и уравнение (1.37), найдем его

общее решение в виде u = Cex2 ,	где C - произвольная постоянная, а положив
C =1, найдем частное решение
u = ex2 .							(1.44)
Подставив (1.44) в уравнение	(1.42),	сможем		написать e	x2	3	x2	или
						v ' = 4x e
v' = 4x3 , откуда в результате интегрирования получим
v = x4 +C,								(1.45)
где C - произвольная постоянная. Подставляя (1.44) и (1.45) в (1.41), получим
то же самое решение, что и по методу Лагранжа.
Решение задач
	dy	x(1 − y2 )
Задача 1.1. Решить уравнение	dx =			при x ≥ 2 .
		(x2 −1) y

Данное дифференциальное уравнение есть уравнение с разделяющимися

x

1− y2

'

= −

y2 +1

переменными. Функции

и

непрерывны при любых

x2 −1

y

y2

y

значениях x ≥ 2 и y ≠ 0 .

Считая пока, что 1− y2 ≠ 0

и умножив обе части данного уравнения на

дробь

ydx

, получим:

1− y2

x

dx +

y

dy = 0.

(1.46)

1− x2

1− y2

Умножая уравнение

(1.46)

на

число

(−2)

и

замечая, что

при этом в

числителе каждой дроби стоит производная знаменателя, сможем написать в

результате интегрирования	ln |1− x2 | +ln |1− y2 |= ln C,			где	произвольная
постоянная обозначена через		ln C , что	возможно,	если	принять C > 0 .
Последнее равенство можно записать в виде			|1− x2 | |1− y2 |= C. Мы получили
общий интеграл данного уравнения при условии 1− y2 ≠ 0.
Рассмотрим теперь случай		1− y2 = 0 ,	т.е. y = ±1.	Непосредственно из
данного уравнения видно,	что	каждый из	случаев y =1 и		y = −1 является

решением. При этом они содержатся в общем интеграле и могут быть получены из него при C = 0 .

27

Задача 1.2. Решить уравнение		xyy '+ x2 −1 = 0		при x >1 .
Для установления типа данного уравнения умножим обе его части на					1	.
					x
Получим уравнение	yy′ =	1− x2	, которое	является уравнением		с
		x

разделяющимися переменными.

Для решения последнего уравнения умножим обе части на dx . Будем иметь

1− x2

1

ydy =

x

dx

или в таком виде: ydy =

− x dx .

x

Выполняя операции интегрирования, сможем написать

y2

= ln x −

x2

+C, где

2

2

C -

произвольная постоянная. Разрешая относительно

y2 ,

получим

окончательно

y2 = 2ln x − x2 +C, где произведение 2C вновь обозначено через

C .

Задача 1.3. Для x ≥ 2 найти решение уравнения

y′ =

x2 +3y2

,

(1.47)

2xy

удовлетворяющее начальному условию y(2) = 2 .

Вначале заметим, что правая часть данного уравнения является однородной функцией нулевой степени и, кроме того, она непрерывна и не обращается в нуль в любой области D , не содержащей начала координат системы Oxy .

Введем

подстановку y = xu(x) ,

где

u

- новая

неизвестная функция

x .

Уравнение (1.47) при этом имеет вид

u + xu′

=

x2

+3x2u2

.

2xxu

x2 ,

Сократив в правой части уравнения на отличный от нуля множитель

получим x

du

=

1

+3u2

−u . Упростив и разделив переменные, сможем написать

dx

2u

dx

2udu

=

. Выполняя интегрирование, будем иметь

ln x = ln(1+u2 ) +ln C,

где

x

1+u2

C - произвольное положительное число. Из последнего равенства следует,

что

x = C(1+u2 ).

y ,

Возвращаясь к искомой функции

получим общий интеграл уравнения

(1.47) в виде

x = C

y

2

1+

.

(1.48)

x2

Для отыскания частного интеграла, удовлетворяющего заданному

начальному условию,

положим в

(1.48)

x = 2, y = 2 . Получим C =1 . Если

28

подставить C =1 в равенство (1.48), то сможем записать искомый частный

интеграл в виде	y2 = x3 − x2 .
Задача 1.4.	Найти решение уравнения	(1+ x2 ) y '−2xy = (1+ x2 )2 ,

удовлетворяющее начальному условию y(1) = 4 .

Приведем данное уравнение к виду (1.25), для чего разделим обе его части

на 1+ x2 . Получим			2x
	y '−					y =1		+ x2.		(1.49)
			+ x2
	1
В нашем случае имеем	p(x) = −				2x		,		q(x) =1 + x2 .
			1 + x2
Для того чтобы найти	общее		решение						уравнения (1.49),	воспользуемся

формулой (1.30), для чего выпишем вначале величины, входящие в нее

∫p(x)dx = −∫

2x

dx = −ln(1 + x

2

),

e

−∫ p(x)dx

= e

ln(1+x2 )

=

1 + x

2

,

1

+ x

2

1

1

e∫ p(x)dx = e−ln(1+x2 ) =

,

∫q(x)e∫ p(x)dxdx = ∫(1 + x2 )

dx = ∫dx = x.

2

+ x

2

1 + x

1

Подставив эти выражения в формулу (1.30), получим

y = (1+ x2 )(x +C) .

(1.50)

Для нахождения искомого частного решения положим в (1.50)

x =1 , а

y = 4 , 4 = 2(1+C) , откуда следует C =1.

Искомое частное решение имеет вид

y = (1+ x2 )(1+ x).

Задача 1.5. Решить уравнение при y > 0

(x +2 y

y cos y) y '−2 y = 0 .

(1.51)

Если считать x за аргумент, а y за функцию,

то это уравнение не является

линейным. Если же за независимую переменную принять

y , а x за искомую

функцию, то данное уравнение можно привести к виду (1.25).

Запишем данное уравнение сначала в виде

(x +2 y y cos y)

dy

= 2 y,

а затем

dx

в виде 2 y dx

− x = 2 y y cos y.

dy

уравнения на 2 y ,

Разделив

обе части

последнего

получим линейное

уравнение относительно неизвестной функции x( y)

dx −

1

x =

y cos y.

(1.52)

2 y

dy

В согласии с формулой (1.30), в которой следует x и

y поменять местами,

получим выражение для общего решения уравнения (1.51)

29

x = e	−∫(2−1)y dy	∫	y cos y e	∫(2−1)y dy

dy +C .

1

ln y

∫

y cos y e

−

1

ln y

Вычисляя интегралы, сможем написать x = e2

2

dy +C или

1

(∫

)

x =

y

y cos y

dy +C

,

откуда следует

x =

y

cos ydy +C

.

∫

y

Вычисляя интеграл, получим окончательно общий интеграл данного

дифференциального уравнения x =

y (sin y +C).

Задача 1.6. Проинтегрировать уравнение y′cos x + y sin x =1 при начальном

условии y(0) =

3

и вычислить значение функции y(x) при x = π .

2

6

Данное

уравнение

- линейное

дифференциальное уравнение

первого

порядка. Запишем его в виде y′+ p(x) y = q(x) , разделив обе части уравнения на cos x (при cos x ≠ 0 ).

y′+ y cossin xx = cos1 x . Здесь p(x) = cossin xx , q(x) = cos1 x .

Воспользуемся формулой общего решения линейного уравнения

Так как ∫

Для cos x

y = e	−∫ p( x)dx		q(x)e	∫ p( x)dx
		∫			dx +C
					.

sin x

d(cos x)

p(x)dx = ∫

dx = −∫

= −ln

cos x

, то

cos x

cos x

ln

cos x

1

−ln

cos x

y = e

e

dx +C .

> 0 имеем

∫cos x

1

1

y = cos x

dx +C .

∫cos x

cos x

			dx		y = cos x (tgx +C ); y = sin x +C cos x .
	y = cos x			+C ;
		∫cos2 x

	Получили общее решение уравнения:							y = sin x +C cos x .
	Решим задачу Коши: найдем частное решение, удовлетворяющее
	начальным условиям				y(0) =	3	, т.е. то значение произвольной постоянной, при
						2
	котором	y(0) =	3	.	Поставим			x = 0 и	y =	3		в общее решение
			2							2
								30

	y = sin x +C cos x .								Получим						3	= sin 0 +C cos 0 ,									отсюда					C =				3	.	Тогда
															2																		2
	y = sin x +		3		cos x		- частное решение, удовлетворяющее начальным условиям.
		2
																				π .
	Вычислим значение функции y(x) в точке x =
																				6
						π			π		3		π				π		1			3		3			1		3		5
				y		= sin				+		cos			;	y		=		+						=		+		=			.
									6		2		6						2			2		2			2		4		4
				6			5									6
	Ответ: y(x)			x=		π =		.
							4
						6																								cos x > 0 ,
	Замечание. При решении задачи вводили ограничение																																				но
	полученное				y = sin x +C cos x								-		общее			решение						является таковым												и	при

cos x < 0 , а cos x = 0 не является вообще решением.

Вопросы для самопроверки по теме 1.2

1.Как в общем виде можно записать дифференциальное уравнение первого порядка с разделяющимися переменными? Сформулируйте метод его интегрирования.

2.Дайте определение однородной функции степени m > 0 и степени m = 0 .

3.Какое уравнение называется однородным дифференциальным уравнением первого порядка?

4.Дайте определение линейного дифференциального уравнения первого порядка.

5.В чем заключается метод Лагранжа (метод вариации произвольной постоянной) интегрирования линейного дифференциального уравнения первого порядка?

6.Сформулируйте метод Бернулли (разделения переменных) для интегрирования линейного уравнения.

Раздел 2. Дифференциальные уравнения высших порядков

Данный раздел содержит следующие темы:

2.1.Основные понятия. Дифференциальные уравнения n -го порядка, допускающие понижение порядка.

2.2.Линейные дифференциальные уравнения n -го порядка. Метод Лагранжа вариации произвольных постоянных.

2.3.Линейные дифференциальные уравнения с постоянными коэффициентами. После изучения теоретического материала следует ответить на вопросы для

самопроверки и на вопросы тестов № 3-5. При возникающих затруднениях в ответах обратитесь к [1].

31

Студентам очно-заочной и заочной форм обучения надо решить две задачи из контрольной работы № 5 под номерами 11-20 и 21-30 в соответствии со своим вариантом.

2.1. Основные понятия. Дифференциальные уравнения n -го

порядка, допускающие понижение порядка

В рассматриваемой теме Вам предстоит ознакомиться со следующими вопросами:

•Решение дифференциального уравнения n -го порядка. Задача Коши для уравнения n -го порядка.

•Дифференциальные уравнения n -го порядка, допускающие понижение порядка.

После изучения теоретического материала следует ответить на вопросы самопроверки и на вопросы теста №3. При возникающих затруднениях в ответах обратитесь к [1].

Студентам очно-заочной и заочной форм обучения надо решить одну задачу из контрольной работы № 5 под номером 11-20 в соответствии со своим вариантом.

Решение дифференциального уравнения n -го порядка. Задача Коши для уравнения n -го порядка

Ранее указывалось, что любое дифференциальное уравнение n -го порядка с одной неизвестной функцией у аргумента x всегда можно записать в виде

F(x, y, y ', y '',..., y(n) ) = 0,

(2.1)

где F означает известную функцию своих аргументов, причем производная y(n) обязательно содержится в уравнении.

Решением дифференциального уравнения (2.1) на промежутке	X
называется всякая функция y =ϕ(x), которая определена и n	раз

дифференцируема на этом промежутке и которая при подстановке в уравнение (2.1) обращает его в тождество на промежутке X

F(x,ϕ(x),ϕ'(x),ϕ''(x),...,ϕ(n) (x)) ≡ 0 .
Если уравнение (2.1) удается разрешить относительно y(n) ,	то его можно
записать в виде
y(n) = f (x, y, y ',..., y(n−1) ),	(2.2)
где f - известная функция своих аргументов, определенная	в некоторой
области D пространства n +1 измерений.
Уравнение вида (2.2) называют уравнением n -го порядка,	разрешенном
относительно старшей производной.

Так же как и дифференциальное уравнение первого порядка, дифференциальное уравнение высшего порядка имеет, вообще говоря,

32

бесконечное множество решений, каждое из которых изображается на

плоскости Oxy	некоторой кривой, которая называется интегральной кривой
соответствующего уравнения.									y = ϕ(x),
Задача Коши для уравнения (2.2) ставится так: найти решение
удовлетворяющее начальным условиям							,..., ϕ(n−1) (x ) = y(n−1) ,
ϕ(x ) = y ,ϕ'(x ) = y			0	',ϕ''(x ) = y ''					(2.3)
0	0	0			0	0	0	0
где x0 , y0 , y '0 ,..., y0(n−1) -		заданные			числа,		которые называют начальными

значениями.

Характерная особенность задачи Коши состоит в том, что начальные условия задаются при одном и том же значении аргумента.

Как и для дифференциального уравнения первого порядка в рассматриваемом случае возникает вопрос о существовании и единственности решения задачи Коши. На этот вопрос отвечает теорема, которую мы приводим без доказательства и в упрощенной формулировке.

Теорема 2.1. Если в уравнении

y(n) = f (x, y, y ', y '',...y(n−1) )

функция f (x, y, y ',..., y(n−1) ) , а так же частные производные

	∂f ,	∂f	,	∂f		,...,	∂f
		∂y '		∂y ''			∂y(n−1)
	∂y
непрерывны в некоторой области D					пространства n +1 измерений, то какова
бы ни была точка	(x0 , y0 , y '0 ,..., y0(n−1) )				этой области, существует единственное
решение y = ϕ(x)	данного уравнения, определенное в некотором интервале,

содержащем точку x0 , и удовлетворяющее начальным условиям

ϕ(x0 ) = y0 ,ϕ'(x0 ) = y '0 ,ϕ''(x0 ) = y ''0 ,..., ϕ(n−1) (x0 ) = y0(n−1).

Отметим специально, что единственность решения задачи Коши для уравнения n -го порядка (2.2) не означает, что через данную точку (x0 , y0 ) плоскости Oxy проходит только одна интегральная кривая, как это имело место

для уравнения первого порядка, разрешенного относительно производной. В частности, для уравнения второго порядка вида (2.2) единственность решения

задачи Коши означает, что через точку (x0 , y0 ) проходит единственная интегральная кривая, которая в этой точке составляет с положительным направлением оси Ox угол, тангенс которого равен y '0 .

Решение конкретных прикладных задач часто приводит не к начальным условиям типа (2.3), а к так называемым краевым условиям, когда значения искомой функции и ее производных задаются для нескольких различных значений аргумента. Задача отыскания решения дифференциального уравнения, удовлетворяющего такого типа условиям, называется краевой задачей или

граничной.

33

Естественно, что краевые задачи могут ставиться лишь для уравнений выше первого порядка, ибо в случае уравнения первого порядка задание значения искомого решения в одной точке (в силу теоремы 2.1) уже определяет решение в других точках единственным образом и, следовательно, значение решения во второй точке может быть вычислено, а не задаваемо заранее.

Заметим, что краевая задача не всегда имеет решение, а если и имеет, то, как правило, не единственное.

Пример 2.1. Найти решения уравнения y '' = 6x , удовлетворяющие граничным условиям y(−1) = 0, y(1) = 8.

Замечая, что y '' = ( y ') ' , можно данное уравнение записать в виде

( y ') ' = 6x ,

откуда следует y ' = ∫6xdx +C1 , где C1 - произвольная постоянная. Выполняя

интегрирование, получим

y ' = 3x2 +C1.

Интегрируя последнее уравнение, будем иметь y = x3 +C1x +C2 ,

где C2 - произвольная постоянная. Заметим, что все решения данного уравнения содержатся в последней формуле. Выберем постоянные C1 и C2 так,

чтобы заданные граничные условия выполнялись. В результате получим систему уравнений

0 = −1 −C +C ,		или	C −C = −1,
	1 2		1 2
	8 =1 +C1 +C2 ,		C1 +C2 = 7,

откуда следует C1 = 3,C2 = 4 , так что искомое решение будет единственным y = x3 +3x2 +4.

Распространим определение общего решения дифференциального уравнения первого порядка на дифференциальное уравнение n -го порядка вида (2.2). С этой целью обозначим через D некоторую область изменения

переменных x, y, y ', y '',..., y(n−1) , считая, что в каждой ее точке выполнены условия теоремы 2.1.

Определение. Функция
y = ϕ(x,C1,C2 ,...,Cn ),	(2.4)
определенная в некоторой области изменения переменных x,	C1,C2 ,...,Cn и
имеющая непрерывные частные производные по x до	n -го порядка
включительно, называется общим решением уравнения (2.2)	в области D ,
если выполнены два условия:

34

Система уравнений

		y = ϕ(x,C1,C2 ,...,Cn ),
		y ' = ϕ'(x,C ,C		2	,...,C			n	),
		1
		.......											(2.5)
y(n−1) = ϕ(n−1) (x,C ,C						2	,...,C			n	),
				1
разрешима в области D относительно C1,C2 ,...,Cn , так что имеем
C		= Ψ (x, y, y ',..., y(n−1) ),
	1	1
C		= Ψ (x, y, y ',..., y(n−1) ),											(2.6)
	2	2
		.......
C	n	= Ψ (x, y, y ',..., y(n−1) ).
		n
2) Функция (2.4) является решением уравнения									(2.2)			при всех	значениях
C1,C2 ,C3 ,..., Cn доставляемых		формулами	(2.6)					при				условии,	что точка

(x, y, y ',..., y(n−1) ) - произвольная точка области D .

Отметим, что общее решение уравнения содержит в себе все решения уравнения (2.2) с начальными данными из области D . Каждое из них может быть получено из формулы (2.4) при соответствующих значениях постоянных

C1,C2 ,...,Cn .

Решение, получающееся из общего решения при конкретных (допустимых) значениях постоянных C1,C2 ,...,Cn , называют частным решением данного

уравнения.

Чтобы найти частное решение, удовлетворяющее начальным условиям (2.3)

при условии, что точка	(x , y , y ' , y ''				,..., y(n−1) )							принадлежит области D ,
	0	0	0	0			0
следует подставить начальные значения					x0 , y0 , y '0 , y ''0 ,..., y0(n−1) в систему (2.5)
вместо x, y, y ',..., y(n−1) и решить полученную систему
	y0 = ϕ(x0 ,C1,C2 ,...,Cn ),
	y '	= ϕ'(x ,C ,C				2	,...,C			n	),
	0		0	1
			.......
y(n−1)		= ϕ(n−1) (x ,C ,C						2	,...,C			n	),
	0			0	1

относительно постоянных C1,C2 ,...,Cn . Подставив найденные значения в общее

решение (2.4), получим искомое частное решение, удовлетворяющее начальным условиям (2.3).

Общее решение уравнения (2.2), записанное в виде не разрешенном относительно искомой функции y

Φ(x, y,C1,C2 ,...,Cn ) = 0 ,

называется общим интегралом рассматриваемого уравнения.

35

Решение уравнений n -го порядка в некоторых случаях удается провести с помощью понижения его порядка за счет соответствующих замен искомой функции и независимой переменной. Ниже будут рассмотрены некоторые типы уравнений, допускающие понижение порядка.

Дифференциальные уравнения, допускающие понижение порядка

Первый тип. Уравнение вида
y(n) = f (x),	(2.7)

где f (x) - функция, непрерывная на некотором промежутке X . Для этого типа уравнений можно найти общее решение в квадратурах, последовательно понижая порядок уравнения на единицу. Действительно, так как y(n) = ( y(n−1) ) ', то данное уравнение запишем в виде ( y(n−1) ) ' = f (x) , откуда следует

		y(n−1) = ∫ f (x)dx +C1,	(2.8)
где	C	- произвольная постоянная. Учитывая, что	y(n−1) = ( y(n−2) ) ' , проделаем с
	1

уравнением (2.8) те же операции, что и с уравнением (2.7). В результате

получим y(n−2) = ∫∫ f (x)dxdx +C1x +C2 ,

где C2

- произвольная постоянная.

Продолжая так и далее, будем получать последовательно

y(n−3)

= ∫∫∫f (x)dxdxdx +C1

x2

+C2 x +C3 ,

2!

y(n−4)

= ∫∫∫∫f (x)dxdxdxdx +C1

x3

+C2

x2

x

+C3 x +C4 ,

и т.д. Наконец, получим

3!

2!

cn−1

xn−2

y = ∫∫...∫ f (x)dxdx...dx + C1

+ C2

+... + Cn−1x + Cn ,

(n −

1)!

(n − 2)!

где C3,C4 ,..., Cn - появляющиеся последовательно произвольные постоянные. Легко видеть, что это общее решение данного уравнения в области

{x X ,| y |< +∞,| y ' |< +∞,...,| y(n−1) |< +∞}.

Например, уравнения	y′′′ = e2 x , x5 yIV = x +2	и	sin2 x y′′ = cos x -	это
уравнения первого типа.
Второй тип. Уравнение вида
	F(x, y(k ) , y(k+1) ,..., y(n) ) = 0,		(2.9)
где F -заданная функция	своих аргументов,	а	натуральное число	k

удовлетворяет неравенству 1 ≤ k ≤ n −1, т.е. это тип уравнения, не содержащего искомой функции и ее производных до порядка k −1 включительно.

Введем новую неизвестную функцию z(x) , положив
z = y(k ) .	(2.10)
36

Тогда y(k +1)	= z ', y(k +2) = z '',..., y(n) = z(n−k )		и уравнение (2.9) может быть
записано в виде		F(x, z, z ', z '',..., z(n−k ) ) = 0.
					(2.11)
Это дифференциальное уравнение порядка n −k				относительно неизвестной
функции z(x) ,	то есть	порядок понижается	на	k единиц.	Допустим, что
полученное уравнение		(n − k) -го порядка проинтегрировано и получено его
общее решение		z = ϕ( x, C1 , C2 ,..., Cn −k ),			(2.12)

где C1,C2 ,...,Cn−k - произвольные постоянные. Используя подстановку (2.10) и

соотношение (2.12), получим уравнение k -го порядка для определения функции y

y(k ) = ϕ(x,C1,C2 ,...,Cn−k ).

Это уравнение относится к рассмотренному выше первому типу (2.7) и, следовательно, интегрируя его последовательно k раз, получим общее решение

уравнения (2.9) в виде
y = Ψ(x,C1,C2 ,...,Cn ).
Итак, вопрос об интегрировании уравнения n -го	порядка	типа	(2.9)
сводится к интегрированию уравнения (n − k) -го порядка (2.11).
Например, уравнения (x +1)y′′′− y′′ = 0 , y′′ = y′+e3x и	y′′ = −4	(y′)2	- это
уравнения второго типа.
Третий тип. Уравнение вида
F( y, y ', y '',..., y(n) ) = 0,			(2.13)

где F - заданная функция своих аргументов, то есть это тип уравнений, не содержащих явно независимой переменной. Покажем, что порядок уравнения

этого типа может быть понижен на единицу. Для этого примем	y за новую
независимую переменную, а за новую искомую функцию - y ' ,	которую для
удобства обозначим через p так, что сможем написать
y ' = p( y).	(2.14)

В согласии с правилом дифференцирования сложной функции будем иметь:

y '' = dy '

= dp( y) = dp( y)

dy

= dp

p.

(2.15)

dx

dx

dy

dx

dy

Используя полученное выражение, имеем

dy ''

d

dp p =

d

dp

p

2

+ dp

2

y ''' =

=

dy = d

2p p

p.

(2.16)

dx

dx dy

dy dy

dx

dy

dy

Из последних выражений непосредственно видно, что вторая производная от y по x выразилась через первую производную от p по y , а третья производная от y по x выразилась через вторую производную от p по y . Продолжая так и далее, нетрудно убедиться что каждая из производных от y

37

по x порядка m(1 < m ≤ n) выражается через производные от p по									y порядка
не выше m −1 , то есть
	dp		d 2 p		d m−1 p
y(m) = ωm p,		,		,...,			, (1	< m ≤ n),	(2.17)
	dy		dy2
					dym−1

где ωm - известная функция своих аргументов.

Заменяя в уравнении (2.13) производные y ', y '',..., y(n) соответственно выражениями (2.15), (2.16), (2.17), получим дифференциальное уравнение n −1 порядка относительно новой неизвестной функции p аргумента y

F1		dp	,	d 2 p	,...,	d n−1 p		= 0,	(2.18)
	y, p,	dy		dy2		dyn−1

где F1 - известная функция своих аргументов.

Если последнее уравнение проинтегрировано и его общее решение имеет вид

p = ϕ( y,C1,C2 ,...,Cn−1),

где ϕ известная функция своих аргументов, а C1,C2 ,...,Cn−1 - произвольные

постоянные, то решение данного уравнения сводится к решению уравнения первого порядка.

Интегрируя последнее уравнение, получим общий интеграл уравнения

(2.13)

dy

∫ϕ( y,C1,C2 ,...,Cn−1) = x +Cn ,

где Cn - произвольная постоянная.

Из изложенного следует, что интегрирование уравнения n -го порядка типа (2.13) с помощью подстановки (2.14) сводится к интегрированию уравнения (n −1) -го порядка (2.18).

	Например, уравнения (1+ y2 )y′′−2 yy′2 = 0 ,	yy′′ = (y′)2 − y′ и		y′′ = −	1	- это
					y′
	уравнения третьего типа.
	Решение задач
	Задача 2.1. Найти решение уравнения	y ''' = e2 x ,	удовлетворяющее
	начальным условиям
	y(0) = 0, y '(0) =1, y ''(0) = 2.					(2.19)

Это уравнение рассмотренного первого типа. Так как функция f (x) = e2 x непрерывна на всей оси Ox , то общее решение может быть получено после трехкратного последовательного интегрирования функции e2x , а именно

	y '' = ∫e2 xdx +C1 =	1	e2 x +C1,	(2.20)
		2
	38

y ' =	∫		1	e	2 x		=	1	e	2 x	+C1x +C2	,	(2.21)
			2			+C1 dx +C2		4

∫

1

2 x

1

2 x

x2

y =

e

+C1x +C2 dx +C3

=

e

+C1

+C2 x +C3 ,

(2.22)

8

2

4

где C1,C2 ,C3 - произвольные постоянные.

Для получения частного решения, удовлетворяющего начальным условиям (2.19), подставим в выражения (2.20), (2.21), (2.22) соответствующие начальные значения. В результате получим следующие уравнения для определения

постоянных C1,C2 ,C3 :

2 =		1		+C1, 1 =												1				+C2 , 0 =											1			+C3 ,
	2															4
																													8
откуда следует, что	C1 =					3			,			C2			=			3			,			C3			= −		1			.
																													8
	2															4
Искомое частное решение имеет вид
				y =			1				e	2 x		+			3			x		2	+		3		x −			1			.
							8									4									4				8
Задача 2.2. Решить уравнение (x +1) y '''− y '' = 0 , считая, что x > 0 .
Данное уравнение не содержит неизвестной функции																																				y и ее производной
y ', следовательно, оно относится ко второму типу. Введя подстановку
											z = y '',													(x +1)z '− z = 0.												(2.23)
получим уравнение первого порядка:																																				Это уравнение с
разделяющимися переменными, так что можем записать его в виде
			dz								z													dz			=	dx
					=										или																				.
			dx					x +1																z				x +1

Интегрируя последнее уравнение, получим его общее решение для случая

z > 0
z = C1(x +1),	(2.24)

где C1 - произвольная положительная постоянная. Из равенств (2.23) и (2.24) следует

y '' = C1(x +1),

т. е. дифференциальное уравнение второго порядка первого типа.

Выполняя последовательно двукратное интегрирование функции C1(x +1) ,

получим	(x +1)2		+C2 ,	и общее решение данного уравнения
	сначала y ' = C1	2!
y = C1	(x +1)3	где C2 и C3		- произвольные постоянные.
	+C2 x +C3 ,

3!

Задача 2.3. Решить уравнение

(1+ y2 ) y ''−2 yy '2 = 0.

39

Данное уравнение имеет второй порядок и не содержит явно независимой

переменной x и, следовательно, относится

к третьему

типу. Если ввести

подстановку y ' = p,

считая p функцией y , то

y '' = dy '

= dp

= dp dy

= dp

p,

dx

dx

dy dx

dy

а тогда данное уравнение можно записать в виде

2

dp

2

2

dp

(1 + y

)

p − 2 yp

= 0 или p (1 + y

)

− 2 yp

= 0 .

dy

dy

Это дифференциальное уравнение распадается на два: p = 0, (1+ y2 ) dpdy −2 yp = 0.

Первое из них дает y ' = 0 , т.е. y = C , где C - произвольная постоянная.

Разделив обе части второго уравнения на 1+ y2 , получим линейное однородное уравнение первого порядка

dpdy −1+2 yy2 p = 0.

Воспользовавшись формулой (1.27) для общего решения линейного однородного уравнения первого порядка, можем написать

		2 y
	−
−∫		1+y	2	dy
p = C e				,
1

где C1 - произвольная постоянная. Выполняя интегрирование, получим

p = C1eln(1+y2 ) = C1(1+ y2 ).

Вспоминая, что p = y ' будем иметь уравнение первого порядка с разделяющимися переменными

y ' = C (1 + y2 )	или		dy	= C dx.
1	1		+ y2	1
Выполняя интегрирование, получим
arctgy = C1x +C2 ,
где C2 - произвольная постоянная. Замечая,			что решение		y = C содержится в
последнем выражении при C1 = 0 ,	можем		утверждать,		что это выражение

представляет собою общий интеграл данного уравнения.

Вопросы для самопроверки по теме 2.1

1.Какое уравнение называется обыкновенным дифференциальным уравнением n -го порядка?

2.Какая функция называется решением дифференциального уравнения n -го порядка?

3.Как ставится задача Коши для дифференциального уравнения n -го порядка?

40

4.Чем отличаются начальные условия и краевые условия для дифференциального уравнения n -го порядка?

5.Как определяется общее решение уравнения n -го порядка?

6.Какие типы дифференциальных уравнений n -го порядка допускают понижение порядка?

2.2.Линейные дифференциальные уравнения n -го порядка.

Метод Лагранжа вариации произвольных постоянных

В рассматриваемой теме Вам предстоит ознакомиться со следующими вопросами:

•Однородные и неоднородные линейные дифференциальные уравнения.

•Структура общего решения линейного однородного дифференциального уравнения n -го порядка ;

•Метод Лагранжа вариации произвольных постоянных.

После изучения теоретического материала следует ответить на вопросы для самопроверки и на вопросы теста №4. При возникающих затруднениях в ответах обратитесь к [1].

Однородные и неоднородные линейные дифференциальные уравнения. Структура общего решения линейного однородного дифференциального уравнения n -го порядка

Определение. Линейным дифференциальным уравнением n -го порядка называется уравнение вида

		y(n) + p (x) y(n−1) + p (x) y(n−2) +... + p					(x) y '+ p (x) y = f (x),			(2.25)
		1		2		n−1		n
где	y	-	искомая	функция		аргумента		x ,	а	функции
p1(x), p2 (x),..., pn−1(x), pn (x), f (x)					заданы	и	непрерывны		на	некотором
промежутке (a, b).
	Если всюду в (a, b) функция				f (x) тождественно равна нулю, то уравнение

(2.25) называется однородным, или линейным уравнением без правой части, в противном случае неоднородным, или линейным уравнением с правой частью.

Если уравнение (2.25) разрешить относительно старшей производной, то легко заметить, что в области

{a < x <b, −∞ < y < +∞, −∞ < y ' < +∞,..., −∞ < y(n−1) < +∞}

n +1- мерного пространства выполнены все условия теоремы о существовании и единственности решения задачи Коши. Это значит, что для любого x0 из

(a, b) всюду на (a, b)	существует единственное решение ϕ(x) уравнения (2.25),
удовлетворяющее начальным условиям
ϕ(x0 ) = y0 ,	ϕ'(x0 ) = y0′, ϕ''(x0 ) = y0′′, ... ϕ(n−1) (x0 ) = y0(n−1) ,
	41

где y0 , y0′, y0′′,..., y0(n−1) - произвольные числа.

Отсюда следует, что общее решение уравнения (2.25) содержит все решения этого уравнения. Особых решений линейное уравнение не имеет.

Рассмотрим подробнее однородное дифференциальное уравнение

y(n) + p1(x) y '+ p2 (x) y ''+... + pn−1(x) y '+ pn (x) y = 0.

(2.26)

Решения линейного однородного уравнения обладают двумя важными свойствами, выражаемыми следующими теоремами

Теорема 2.2. Если функция ϕ(x) является решением уравнения (2.26), а C - любая постоянная, то и функция Cϕ(x) есть также решение уравнения (2.26).

Теорема 2.3. Если функции ϕ1(x) и ϕ2 (x) являются решениями уравнения (2.26), то и их сумма ϕ1(x) + ϕ2 (x) также является решением уравнения (2.26).

Доказательство теорем 2.2 и 2.3 Вы найдете в [1].

Пример 2.2. Задано линейное однородное дифференциальное уравнение

y ''− y '−2 y = 0.
Убедимся вначале, что функция y = e2 x является его решением.	Так как
y ' = 2e2 x , y '' = 4e2 x , то, подставив y = e2 x в левую часть уравнения,	получим

4e2x −2e2x −2e2x ≡ 0.

Умножим теперь это решение на произвольную постоянную C и подставим

произведение Ce2x в данное уравнение. Будем иметь тождество

C4e2x −C2e2x −2Ce2 x ≡ 0 .

Точно также легко убедиться, что	функция e−x является решением
рассматриваемого уравнения. Составим	сумму этих решений e2x +e−x и

подставим в левую часть уравнения. Получим

(e2 x +e−x ) ''−(e2 x +e−x ) '−2(e2 x +e−x ) = = 4e2 x +e−x −2e2 x +e−x −2e2 x −2e−x ≡ 0.

Из изложенного следует, что и линейная комбинация C1e2 x +C2e−x , где C1 и C2

- произвольные постоянные, также является решением предложенного уравнения.

На основании рассмотренных свойств можно утверждать, что, вообще, если функции

ϕ1(x),ϕ2 (x),...,ϕn (x)

(2.27)

являются решениями однородного уравнения (2.26), то их линейная комбинация

C1ϕ1(x) +C2ϕ2 (x) +... +Cnϕn (x),

(2.28)

где C1,C2 ,...,Cn - произвольные постоянные, также является решением этого

уравнения. Естественно возникает вопрос о том, что если число функций n равно порядку однородного уравнения (2.26), то не будет ли линейная комбинация (2.28) общим решением уравнения (2.26) в соответствующей

42

области. Оказывается, что это так, но только если решения (2.27) удовлетворяют некоторому дополнительному условию. Чтобы сформулировать это условие введем понятия линейной зависимости и линейной независимости функций.

Определение. Функции
ϕ1(x),ϕ2 (x),...,ϕn (x)	(2.29)

определенные и непрерывные на интервале (a, b) называются линейно зависимыми на интервале (a, b) , если существует такой набор чисел α1,α2 ,...,αn , среди которых хотя бы одно отлично от нуля, и такие, что при

любом x на интервале (a, b) выполняется тождество
α1ϕ1(x) + α2ϕ2 (x) +... + αnϕn (x) ≡ 0.	(2.30)
Если же тождество (2.30) может быть выполнено только	при условии

α1 = α2 =... = αn = 0 , то функции (2.29) называют линейно независимыми на интервале (a, b) .

Легко видеть, что если функции (2.29) линейно зависимы на (a, b) то, по

крайней мере, одна из этих функций может быть выражена в виде линейной комбинации остальных. Действительно, так как в соотношении (2.30) в этом случае хотя бы один из коэффициентов отличен от нуля, то приняв, для

определенности, что αn ≠ 0 , запишем его в виде

αnϕn (x) = −α1ϕ1(x) −α2ϕ2 (x) −... −αn−1ϕn−1(x).

Разделив обе части последнего равенства на αn , получим

ϕ

(x) = −

α1

ϕ

(x) −

α2

ϕ

(x) −... −

αn−1

ϕ

(x),

n

α

n

1

α

n

2

α

n

n−1

откуда и следует справедливость сделанного утверждения.

Последнее утверждение иногда принимают за определение линейно зависимых функций. При этом, естественно, данное выше определение становится следствием.

Для двух линейно зависимых функций				ϕ1(x)	и	ϕ2 (x)	последнее
утверждение		выглядит так:	ϕ2 (x) = αϕ1(x) ,	т.е.	отношение		ϕ2		(x) = α
			ϕ2 (x)				ϕ1		(x)
(постоянному числу). Поэтому,										то
			если ϕ (x) не равно постоянному числу,
			1
ϕ1(x) и	ϕ2 (x)	линейно независимы. Например,		функции e2x и e−2x ,				sin 3x		и
cos 3x ,	e2x и xe2x - линейно независимы на всей оси Ox .
Пример 2.3. Три функции ϕ1(x) = sin2 x, ϕ2 (x) = cos2 x,						ϕ3 (x) =1		линейно

зависимы на любом интервале, ибо, положив α1 =1,α2 =1,α3 = −1, получим на основании известного тождества из тригонометрии, что

1 sin2 x +1 cos2 x +(−1) 1 ≡ 0.

43

Пример 2.4. Четыре функции 1, x, x2 , x3 линейно независимы на любом промежутке числовой оси, ибо если составить линейную комбинацию этих функций с произвольными коэффициентами α1,α2 ,α3,α4 , то получим

многочлен α1 + α2 x + α3 x2 + α4 x3 , который может обратиться в нуль не более чем при трех значениях x (кубическое уравнение не может иметь более трех вещественных корней). Следовательно, тождество α1 + α2 x + α3x2 + α4 x3 ≡ 0 может быть выполнено, только если α1 = α2 = α3 = α4 = 0.

Считая, что функции (2.29) дифференцируемы n раз на интервале (a, b) , введем в рассмотрение определитель n -го порядка

	ϕ1	ϕ2	...	ϕn
W =	ϕ'1	ϕ'2		ϕ'n	,
	...	...	...	...
	ϕ(n−1)	ϕ(n−1)		ϕ(n−1)
	1	2		n

который называют определителем Вронского (вронскианом) для рассматриваемых функций. Естественно, что определитель Вронского также

является функцией от x , определенной на интервале (a, b).

Оказывается, что с помощью определителя Вронского можно сформулировать довольно удобный признак линейной независимости n решений однородного линейного уравнения n -го порядка. Этот признак дается с помощью следующей теоремы, которую мы сформулируем без доказательства.

Теорема 2.4. Для того чтобы n решений ϕ1,ϕ2 ,...,ϕn линейного однородного уравнения (2.26) были линейно независимы на (a, b), необходимо и достаточно, чтобы определитель Вронского для этих решений не обращался в нуль ни в одной точке из (a,b) .

Использование этого признака облегчается наличием двух важных свойств вронскиана, которые мы примем без доказательства.

1)Если определитель Вронского для этих решений обращается в нуль в одной точке интервала (a, b), то он равен нулю во всех точках (a,b) .

2)Если определитель Вронского для этих решений не равен нулю в одной точке интервала (a, b), то он отличен от нуля во всех точках (a,b) .

Из изложенного следует, что для линейной независимости n решений линейного однородного уравнения n -го порядка на интервале (a, b), необходимо и достаточно, чтобы вронскиан этих решений был отличен от нуля в одной точке интервала (a,b) .

Введем теперь понятие фундаментальной системы решений.

Определение. Фундаментальной системой решений линейного однородного уравнения n -го порядка на интервале (a, b), называется любая система из n решений этого уравнения линейно независимых на (a,b) .

44

Легко видеть, что уравнение (2.26) имеет на интервале (a,b) бесконечное

множество фундаментальных систем решений.

Теперь мы в состоянии ответить на вопрос об условиях, при которых линейная комбинация (2.28) будет общим решением уравнения (2.26).

Имеет место следующая теорема, которую мы примем без доказательства. Теорема 2.5. Если ϕ1,ϕ2 ,...,ϕn - фундаментальная система решений

уравнения (2.26) на интервале (a, b), то линейная комбинация этих решений y = C1ϕ1 +C2ϕ2 +... +Cnϕn ,

где C1,C2 ,...,Cn - произвольные постоянные, является общим решением уравнения (2.26) в области

{a < x < b, −∞ < y < +∞, −∞ < y ' < +∞,..., −∞ < y(n−1) < +∞}.

Пример 2.5. Решить уравнение y ''−2 y '+ y = 0 .

Убедимся вначале, что функции ϕ1 = ex и ϕ2 = xex являются решениями данного уравнения на всей оси. С этой целью подставим в левую часть уравнения сначала функцию ex , а затем xex . Получим

(ex ) ''−2(ex ) '+ex = ex −2ex +ex ≡ 0,

(xex ) ''−2(xex ) '+ xex = 2ex + xex −2(ex + xex ) + xex ≡ 0.

Для того чтобы убедиться, что эти решения линейно независимы на Ox и, следовательно, образуют фундаментальную систему решений, составим определитель Вронского для них

W =

ex

xex

=

ex

xex

= ex ex

1

x

= e2 x (1

+ x − x) = e2 x ≠ 0.

(ex ) ' (xex ) '

ex

ex + xex

1

1+ x

Поскольку вронскиан для этих решений отличен от нуля всюду на Ox , то в согласии с теоремой 2.5, линейная комбинация

y = C1ex +C2 xex ,

где C1 и C2 - произвольные постоянные, представляет собою общее решение данного уравнения в области

{−∞ < x < +∞, −∞ < y < +∞}.

Метод Лагранжа вариации произвольных постоянных

Обратимся к рассмотрению линейных неоднородных дифференциальных уравнений вида

y(n) + p1(x) y(n−1) + p2 (x) y(n−2) +... + pn−1(x) y '+ pn (x) y = f (x),	(2.31)
где y - искомая функция аргумента x , а функции p1(x), p2 (x),...,	pn−1(x),
pn (x), f (x) заданы и непрерывны на некотором интервале (a, b) .

Введем в рассмотрение линейное однородное уравнение, левая часть которого совпадает с левой частью неоднородного уравнения (2.31),

45

y(n) + p (x) y(n−1)		+ p (x) y(n−2) +... + p		n−1	(x) y '+ p (x) y = 0.	(2.32)
	1	2			n
Уравнение	вида	(2.32)	называют		однородным	уравнением,

соответствующим неоднородному уравнению (2.31).

Имеет место следующая теорема о структуре общего решения неоднородного линейного уравнения (2.31).

Теорема 2.6. Общее решение линейного неоднородного уравнения (2.31) в

области {a < x < b, −∞ < y < +∞, −∞ < y ' < +∞,..., −∞ < y(n−1) < +∞}

(2.33)

есть сумма любого его частного решения и общего решения соответствующего однородного уравнения (2.32) в области (2.33), т.е.

y = ϕ+C1ϕ1 +C2ϕ2 +... +Cnϕn ,	(2.34)
где ϕ - частное решение уравнения (2.31), ϕ1,ϕ2 ,...,ϕn	- фундаментальная

система решений однородного уравнения (2.32), а C1,C2 ,...,Cn - произвольные

постоянные.

Доказательство этой теоремы Вы найдете в [1].

На примере дифференциального уравнения второго порядка изложим метод, при помощи которого можно найти частное решение линейного неоднородного уравнения. Этот метод называют методом Лагранжа вариации произвольных постоянных.

Итак, пусть дано неоднородное линейное уравнение

	y ''+ p1 y '+ p2 y = f ,	(2.35)
где коэффициенты p1(x), p2 (x)	и правая часть f (x)	непрерывны в некотором
интервале (a, b) .
Обозначим через ϕ1(x) и	ϕ2 (x) фундаментальную систему решений
однородного уравнения	y ''+ p1 y '+ p2 y = 0.	(2.36)
Тогда его общее решение имеет вид
	y = C1ϕ1 +C2ϕ2 ,	(2.37)

где C1 и C2 - произвольные постоянные.

Будем искать решение уравнения (2.35) в таком же виде, как и общее решение соответствующего однородного уравнения, заменяя произвольные

постоянные некоторыми дифференцируемыми функциями от	x (варьируем
произвольные постоянные), т.е.
ϕ = C1(x)ϕ1 +C2 (x)ϕ2 ,	(2.38)

где C1(x) и C2 (x) - некоторые дифференцируемые функции от x , которые пока

неизвестны и которые попытаемся определить так, чтобы функция (2.38) была бы решением неоднородного уравнения (2.35). Дифференцируя обе части равенства (2.38), получим

ϕ′ = C '1(x)ϕ1 +C1(x)ϕ'1+C '2 (x)ϕ2 +C2 (x)ϕ'2 .

46

Чтобы при вычислении ϕ′′ не появились производные второго порядка от

C1(x) и C2 (x) , потребуем, чтобы всюду в (a, b) выполнялось условие
C '1(x)ϕ1 +C '2 (x)ϕ2 = 0.	(2.39)
Тогда для ϕ′ будем иметь
ϕ′ = C1(x)ϕ'1+C2 (x)ϕ'2 .	(2.40)
Вычислим вторую производную
ϕ′′ = C '1(x)ϕ'1+C1(x)ϕ''1+C '2 (x)ϕ'2 +C2 (x)ϕ''2 .	(2.41)

Подставляя выражения дляϕ , ϕ′, ϕ′′ из (2.38), (2.40), (2.41) в уравнение (2.35), получим

C'1(x)ϕ'1+C1(x)ϕ''1+C'2(x)ϕ'2 +C2(x)ϕ''2 +

+p1[C1(x)ϕ'1+C2 (x)ϕ'2 ]+ p2 [C1(x)ϕ1 +C2 (x)ϕ2 ]= f

или

C1(x)[ϕ''1 + p1ϕ'1 + p2ϕ1 ]+C2 (x)[ϕ''2 + p1ϕ'2 + p2ϕ2 ]+C1′(x)ϕ'1 +C2′(x)ϕ'2 = f . (2.42)

Выражения, стоящие в квадратных скобках, равны нулю всюду в (a, b) , так как ϕ1 и ϕ2 - частные решения уравнения (2.36). При этом (2.42) примет вид C '1(x)ϕ'1+C '2 (x)ϕ'2 = f . Объединяя это условие с условием (2.39), получим систему уравнений для определения C '1(x) и C '2 (x)

C ' (x)ϕ +C ' (x)ϕ				= 0,	(2.43)
	1 1	2	2
C '1(x)ϕ'+C '2 (x)ϕ'2 = f .

Последняя система представляет собой систему двух алгебраических линейных неоднородных уравнений относительно C '1(x) и C '2 (x) . Определителем этой системы является определитель Вронского для фундаментальной системы решений ϕ1 , ϕ2 и, следовательно, отличен от нуля всюду в (a, b) . Это означает, что система (2.43) имеет единственное решение. Решив ее любым способом относительно C '1(x) , C '2 (x) найдем

C '1(x) = Ψ1(x), C '2 (x) = Ψ2 (x),

где Ψ1(x) и Ψ2 (x) - известные функции.

Выполняя интегрирование и учитывая, что в качестве C '1(x) , C '2 (x)

следует брать одну какую-нибудь пару функций, положим постоянные интегрирования равными нулю. Получим

C1 (x) = ∫Ψ1 (x)dx, C2 (x) = ∫Ψ2 (x)dx.

(2.44)

Подставив выражения (2.44) в соотношения (2.38), сможем записать искомое решение неоднородного уравнения (2.35) в виде

y = ϕ1 ∫Ψ1(x)dx + ϕ2 ∫Ψ2 (x)dx.

Этот метод можно обобщить для нахождения частного решения линейного неоднородного уравнения n -го порядка.

47

	Пример 2.6. Решить уравнение			y ''−2 y '+ y =	ex	при	x ≥1, если функции
					x2
	ϕ1 = ex ,	ϕ2 = xex ,
			образуют	фундаментальную			систему	решений

соответствующего однородного уравнения.

Найдем частное решение данного уравнения. Для этого в согласии с методом Лагранжа следует сначала решить систему (2.43), которая в нашем

	exC'		+ xexC'		= 0,
		1		2
случае имеет вид								ex			Сократив обе части каждого из
	exC1'	+ (1 + x)exC2' =							.
								x2
				C' + xC'		= 0,
уравнений на ex , получим				1	2
		C'		+ (1 + x)C'				=		1	.
			1			2				x2

Вычитая почленно из второго уравнения первое, найдем C2' = x12 , а тогда из первого уравнения следует C1' = − 1x . Выполняя интегрирование и полагая

постоянные

интегрирования

равными

нулю,

будем

иметь

C (x) = −ln x, C (x)

= −

1

.

1

2

x

Частное решение данного уравнения можно представить в виде

ϕ = (−ln x)e

x

1

x

,

ϕ=-e

x

ln x − e

x

.

+ −

xe

x

Общее решение данного уравнения имеет при этом вид

y = C ex +C xex

−ex ln x −ex ,

1

2

где C1 и C2 - произвольные постоянные.

Отметим, наконец, одно замечательное свойство, которое часто называют принципом наложения решений и описывают следующей теоремой.

Теорема 2.7. Если на промежутке (a, b) функция ψ1(x) - частное решение

уравнения	y(n) + p1 y(n−1) +... + pn−1 y '+ pn y = f1,							а функция		ψ2 (x)	частное
решение уравнения			y(n) + p1 y(n−1) +... + pn−1 y '+ pn y = f2 ,						то	на	этом же
промежутке	функция		ψ1(x) + ψ2 (x) есть					частное	решение		уравнения
y(n) + p y(n−1)	+... + p	y '+ p		y = f	+ f	2	.
1	n−1		n	1

Вопросы для самопроверки по теме 2.2

1.Какое дифференциальное уравнение называется линейным дифференциальным уравнением n -го порядка?

2.Какое линейное дифференциальное уравнение называется однородным?

48

3.Какими свойствами обладают решения однородного дифференциального уравнения?

4.Дайте определения линейно зависимой и линейно независимой на промежутке [a, b] систем функций ϕ1(x), ϕ2 (x),...,ϕn (x) .

5.Какое условие является необходимым и достаточным, чтобы n решений ϕ1(x), ϕ2 (x),...,ϕn (x) линейного однородного дифференциального уравнения

были линейно независимы на промежутке [a, b]?

6.Что называется фундаментальной системой решений линейного однородного уравнения n -го порядка?

7.Сформулируйте теоремы о структуре общего решения линейного однородного и неоднородного уравнений.

2.3. Линейные дифференциальные уравнения с постоянными коэффициентами

В рассматриваемой теме Вам предстоит ознакомиться со следующими вопросами:

•Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера.

•Линейные неоднородные дифференциальные уравнения n -го порядка.

Метод неопределенных коэффициентов.

После изучения теоретического материала следует ответить на вопросы для самопроверки и на вопросы теста №5. При возникающих затруднениях в ответах обратитесь к [1].

Студентам очно-заочной и заочной форм обучения надо решить одну задачу из контрольной работы № 5 под номерами 21-30 в соответствии со своим вариантом.

Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера

Рассмотрим линейное однородное уравнение n -го порядка

y(n) + p1 y(n−1) + p2 y(n−2) +... + pn−1 y '+ pn y = 0,

(2.45)

где коэффициенты p1, p2 ,..., pn постоянны.

Л.Эйлер показал, что для уравнения (2.45) всегда можно построить фундаментальную систему решений, состоящую из элементарных функций, и, следовательно, оно всегда интегрируется в элементарных функциях. Ниже это утверждение доказывается для уравнения второго порядка, и формулируются

окончательные результаты для уравнения n -го порядка.
Рассмотрим уравнение второго порядка
y ''+ p1 y '+ p2 y = 0,	(2.46)
49

где p1 и p2 - любые вещественные числа.
Следуя Л.Эйлеру, будем искать решения уравнения (2.46) в виде
y = eλx ,	(2.47)

где λ- некоторое число, которое постараемся подобрать так, чтобы функция (2.47) удовлетворяла уравнению (2.46).

Так как y ' = λeλx , а y '' = λ2eλx , то, подставив (2.47) в левую часть уравнения

(2.46), получим

λ2eλx + p λeλx + p eλx = 0 или		eλx (λ2 + p λ + p ) = 0.
1	2	1	2

Множитель eλx отличен от нуля, следовательно, число λ должно быть

корнем уравнения
λ2 + p1λ + p2 = 0.	(2.48)

Это уравнение называется характеристическим уравнением уравнения (2.46), а его корни - характеристическими числами уравнения (2.46).

Заметим, что характеристическое уравнение (2.48) может быть составлено по данному уравнению (2.46), если заменить в нем y '', y ' и y соответственно

на λ2 ,λ и 1.

Уравнение (2.48) является квадратным и, следовательно, имеет два корня,

						p			p	2
которые мы обозначим через	λ	и	λ	2 .	λ = −	1	±		1		− p
	1				1,2	2			2		2 .

Структура фундаментальной системы решений зависит от вида корней характеристического уравнения.

Возможен один из трех случаев:

1)λ1,λ2 - вещественные и различные, D = p1 2 − p2 > 0;

2

2)λ1,λ2 - вещественные и равные, D = p1 2 − p2 = 0;

2

3)λ1,λ2 - комплексные, D = p1 2 − p2 < 0.

2

Перейдем к построению общего решения уравнения (2.46) в каждом из этих случаев.

1) Подставляя в формулу (2.47) вместо λ корни λ1 и λ2 , получим два частных решения уравнения (2.46)

y1 = eλ1x , y2 = eλ2 x.						(2.49)
Эти решения, очевидно, линейно независимы, так как их отношение
	y		eλ2 x		λ2	−λ1) x
	2	=		= e(
	y		λ x
			e 1
1
			50

отлично от постоянной. Кроме того, в линейной независимости решений (2.49) можно убедиться с помощью определителя Вронского. Имеем

W =

eλ1x

eλ2 x

λ

x

e

λ

2

x

1 1

= e

(λ +λ

2

) x

(λ

− λ ) ≠ 0.

= e 1

1

2

λ eλ1x

λ

eλ2 x

λ1 λ2

1

1

2

Итак, решения (2.49) образуют фундаментальную систему решений уравнения (2.46) и, следовательно, его общее решение можно записать в виде

y = C1eλ1x + C2eλ2 x ,

где C1 и C2 - произвольные постоянные.

2) В этом случае дискриминант квадратного уравнения (2.48) равен нулю,

т.е.

p2
1	− p	= 0	,	(2.50)
4	2

и, следовательно, λ1 = λ2 = − p21 .

Одно решение получается на основании предыдущих рассуждений: это

− p1 x

функция y1 = e 2 .

Теперь возникает вопрос об отыскании второго решения уравнения (2.46), линейно независимого с y1. Непосредственной подстановкой в уравнение (2.46)

можно убедиться в том, что функция y2 = xe	−	p1	x
	2		является решением уравнения

(2.46), причем решение y2 линейно независимо с решением y1, и,

следовательно, они образуют фундаментальную систему решений уравнения (2.46), а его общее решение имеет вид

y = C e	−	p1	x	+ C		xe	−	p1	x	,
	2				2		2
1

где C1 и C2 - произвольные постоянные.

Прежде чем переходить к рассмотрению третьего случая, остановимся на понятии комплексного решения уравнения (2.46).

Пусть в интервале (a, b) даны две вещественные дважды непрерывно дифференцируемые функции u(x) и v(x) аргумента x . Комплексная функция

y(x) = u(x) + iv(x)

называется комплексным решением линейного

однородного уравнения (2.46) в интервале (a, b), если всюду в этом интервале имеет место тождество (u +iv)′′+ p1(u +iv)′+ p2 (u +iv) ≡ 0.

Нетрудно убедиться, что последнее тождество можно записать в виде (u′′+ p1u′+ p2u)+ i(v′′+ p1v′+ p2v) ≡ 0, которое, равносильно двум

u′′+ p1u′+ p2u ≡ 0,	v′′+ p1v′+ p2v ≡ 0.
	51

Отсюда следует, что вещественная и мнимая части комплексного решения линейного однородного уравнения (2.46) являются вещественными решениями этого уравнения.

Наконец, для любых вещественных чисел α и β определим комплексную показательную функцию действительного аргумента x при помощи равенства

	e(α+iβ) x	= eαx (cosβx +isin βx).
Последнюю формулу называют формулой Эйлера.
3) Так как числа p1	и p2 вещественные, то комплексные корни		λ1 и λ2
являются сопряженными и для них можем написать
	λ1 = a +bi, λ2 = a −bi.
Корню λ1 = a +bi	будет	соответствовать комплексное	решение

y = e(a+ib) x , которое с помощью формулы Эйлера может быть записано в виде y = eax cosbx +ieax sin bx.

Поскольку вещественная и мнимая части комплексного решения сами являются вещественными решениями, то получаем два частных решения уравнения (2.46)

y = eax cos bx,	y	2	= eax sin bx,
1

в чем можно убедиться и непосредственной подстановкой их в уравнение

(2.46).

Легко видеть, что эти решения линейно независимы на всей числовой оси

(их отношение отлично от постоянной). Аналогично,					корню	λ2 = a −bi
соответствуют вещественные частные решения eax cos bx,					−eax sin bx, которые
линейно зависимы с решениями, соответствующими корню λ1 = a +bi.
Итак, паре комплексных сопряженных корней					λ1 = a +bi,λ2 = a −bi
соответствует два линейно независимых частных решения eax cos bx,						eax sin bx,
и, следовательно, общее решение уравнения (2.46) в этом случае имеет вид
	y = C eax cos bx +C		eax sin bx,
	1	2
где C1 и C2 - произвольные постоянные.
Пример 2.7. Найти общее решение для каждого уравнения:
1) y ''−5 y '+6 y = 0,	2) y ''−6 y '+9 y = 0,			3) y ''−4 y '+13y = 0.

Каждое из данных уравнений является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Составим характеристическое уравнение для каждого уравнения:

1) λ2 −5λ + 6 = 0,				2) λ2 −6λ +9 = 0,	3) λ2 −4λ +13 = 0.
Найдем корни каждого характеристического уравнения
1) λ =	5 ± 25 − 24	=	5 ±1	, λ1 = 2, λ2 = 3.
			2
2
				52

2)	λ =	6 ± 36 −36		= 3, λ1 = λ2 = 3.
		2
3)	λ =	4 ± 16 −52		=	4 ± 6i	, λ1 = 2 + 3i, λ2 = 2 −3i.
		2			2
Общие решения при этом будут иметь вид:
1) y = C1e2 x +C2e3x ,			2)		y = C1e3x +C2 xe3x , 3)		y = C1e2 x cos 3x +C2e2 x sin 3x,

где C1 и C2 - произвольные постоянные.

Перейдем теперь к построению фундаментальной системы решений для уравнения n -го порядка (2.45). Проводя для уравнения (2.45) рассуждения аналогичные проведенным для уравнения второго порядка (2.46), легко убедиться, что вопрос об отыскании его фундаментальной системы сводится к решению уравнения

λn + p λn−1	+ p λn−2	+... + p	λ + p	n	= 0,	(2.51)
1	2		n−1

которое называется характеристическим уравнением уравнения (2.45) и

которое составляется по тому же правилу, что и характеристическое уравнение для уравнения второго порядка (2.46), а именно: производные от искомой функции заменяются соответствующими степенями λ (искомая функция рассматривается как производная нулевого порядка). Корни уравнения (2.51)

называются характеристическими числами уравнения (2.45). Сформулируем общее правило решения линейного однородного

уравнения n -го порядка:

1)Составляем характеристическое уравнение:

λn + p1λn−1 + p2λn−2 +... + pn−1λ + pn = 0.

2)Находим корни характеристического уравнения λ1,λ2 ,...λn.

3)Находим частные линейно независимые решения уравнения (2.45), руководствуясь тем, что:

а) каждому действительному корню λ кратности k соответствует k

линейно независимых частных решений eλx , xeλx , x2eλx ,..., xk −1eλx ;

б) каждой паре комплексных сопряженных корней a +bi и a −bi кратности k соответствует 2k линейно независимых частных решений

eax cos bx,	xeax cos bx,	x2eax cos bx, ...,	xk −1eax cos bx,
eax sin bx,	xeax sin bx,	x2eax sin bx, ...,	xk −1eax sin bx.

Всего таких частных решений будет ровно n , причем можно показать, что они линейно независимы на всей числовой оси.

4) Составляем линейную комбинацию найденных n решений с произвольными коэффициентами, которая и будет общим решением уравнения (2.45) в области

{−∞ < x < ∞, −∞ < y < +∞, −∞ < y ' < +∞, ..., −∞ < yn−1 < +∞}.

Пример 2.8. Решить уравнение y '''+ 4 y ''+6 y '+ 4 y = 0.

53

Составим характеристическое уравнение λ3 + 4λ2 +6λ + 4 = 0.

Это уравнение имеет три простых корня λ1 = −2, λ2 = −1 +i, λ3 = −1 −i. Вещественному корню λ1 = −2 соответствует частное решение y1 = e−2 x , а паре

комплексных сопряженных корней				λ2 = −1 +i и λ3 = −1 −i соответствует два
линейно независимых частных решения
y	2	= e−x cos x,			y = e−x sin x.
					3
Общее решение будет иметь вид
y = C e−2 x +C				e−x	cos x +C e−x sin x,
	1		2		3

где C1,C2 ,C3 - произвольные постоянные.

Линейные неоднородные дифференциальные уравнения n -го порядка. Метод неопределенных коэффициентов

Перейдем теперь к рассмотрению линейных неоднородных уравнений n -го порядка

y(n) + p y(n−1) + p y(n−2)		+... + p	n−1	y '+ p y = f (x),		(2.52)
1	2				n
где p1, p2 ,..., pn	- вещественные числа,				а функция	f (x) непрерывна в

некотором промежутке (a, b).

Ранее было показано, что общее решение уравнения (2.52) может быть представлено в виде суммы общего решения соответствующего однородного уравнения и произвольного частного решения уравнения (2.52). Правила отыскания общего решения однородного уравнения, соответствующего уравнению (2.52) были изложены выше. Для отыскания частного решения уравнения (2.52) можно использовать метод Лагранжа вариации произвольных постоянных. Но его применение часто приводит к необходимости производить довольно сложные вычисления. Однако, для некоторых случаев, когда правая часть f (x) имеет специальный вид, удается

найти частное решение уравнения (2.52) без квадратур с помощью метода неопределенных коэффициентов.

Метод неопределенных коэффициентов состоит в том, что частное решение неоднородного уравнения (2.52) ищется в виде, определяемом видом правой части уравнения. При этом сначала задается вид частного решения с неопределенными коэффициентами, а затем эти коэффициенты определяются после подстановки этого решения в левую часть уравнения (2.52) и приравнивания коэффициентов при одинаковых степенях x в левой и правой частях полученного равенства.

1) Рассмотрим сначала случай, когда правая часть уравнения (2.52) имеет вид

f (x) = Pm (x)eax ,

(2.53)

где a - вещественное число, а Pm (x) - многочлен степени m .

54

В этом случае частное решение уравнения (2.52) следует искать в виде

y = xk Qm (x)eax

(2.54)

где Qm (x) - многочлен степени m с неопределенными коэффициентами, а k - кратность числа a как корня характеристического уравнения однородного

уравнения соответствующего уравнению (2.52)			(если a не является корнем
указанного характеристического уравнения, то k			считается равным нулю).
Пример 2.9. Решить уравнение y ''−5 y '+6 y = (2x2 +1)ex .								(2.55)
P (x) = 2x2	+1	- многочлен второй степени		m = 2	,	eax = ex	, т.е.	a =1	.
Здесь m

Составляем характеристическое уравнение для соответствующего однородного

уравнения	λ2	− λ +	6	=	0 и находим его корни	λ = 2, λ	2	= 3.
		5				1

Частное решение, соответствующее правой части, ищем в виде (2.54), т.е.

y = (Ax2 + Bx +C )ex .

(2.56)

Здесь Qm (x)

- многочлен

второй

степени

( m = 2 )

с

неопределенными

коэффициентами и, так как корни характеристического уравнения

λ1 = 2 ;

λ2 = 3 ,

не

совпадают

с

числом

a =1

(оно

не

является

корнем

характеристического уравнения), то k = 0 .

Чтобы

найти

числа A, B,C ,

подставим

(2.56)

в

уравнение

(2.55),

предварительно найдя y′

и y′′

y′ = (2Ax + B)ex +(Ax2 + Bx +C )ex ;

y′′ = 2Aex + 2(2Ax + B)ex +(Ax2 + Bx +C )ex .

Получим:

2Aex +2(2Ax +B)ex +(Ax2 +Bx +C)ex −5(2Ax +B)ex −5(Ax2 +Bx +C)ex +

+6(Ax2 +Bx +C)ex =(2x2 +1)ex.

Разделив обе части уравнения на ex , имеем:

2A −3(2Ax + B)+2(Ax2 + Bx +C )= 2x2 +1

или

2 Ax2 +(2B −6 A)x + 2A −3B +C = 2x2 +1 .

Приравнивая коэффициенты при одинаковых степенях

x в левой и правой

части тождества, получим систему уравнений

2A = 2

= 0

, откуда

A =1,

B = 3,

C = 8.

Таким образом,

y = (x2 +3x +8)ex .

2B −6 A

+C =1

2A −3B

Пример 2.10.

Если же требуется решить уравнение

y ''−5y '+6 y = 3e2 x ,

то опять правая часть имеет вид

P (x)eax

,

где

P

(x)

= 3

- многочлен нулевой

m

m

степени;

a = 2 и совпадает с одним из корней характеристического уравнения.

Тогда в уравнении (2.54)

k =1 , а Qm (x) = A - неизвестное число и решение y

55

ищем в виде	y = x1 Ae2 x . Находим	производные y′ = Ae2x + x 2 Ae2x ,
y′′ = 2 Ae2x + 2 Ae2x + 2 Ax 2e2x = 4 Ae2x + 4 Axe2x		и подставляем их в уравнение

y ''−5y '+6x = 3e2 x . Получим 4 Ae2x + 4Axe2x −5(Ae2x + 2xAe2x )+ 6Axe2x = 3e2x .

Сокращая на e2x , имеем 4A +4Ax −5A −10Ax +6Ax = 3; − A = 3; A = −3 и в

этом случае y = −3xe2x .

2) Рассмотрим теперь случай, когда правая часть уравнения (2.52) имеет вид

f (x) = eαx P(1)	(x) cosβx + P(2)	(x)sin βx	,	(2.57)
m	m

где α и β - любые вещественные числа, а Pm(1) (x) и Pm(2) (x) - многочлены от x ,

старшая степень которых равна m .

В этом случае частное решение уравнения (2.52) следует искать в виде

			y = xk eαx Q(1) (x) cosβx +Q(2) (x)sin βx						,	(2.58)
						m	m
где	Q(1)	(x)	и	Q(2)	(x)	-	многочлены степени	m	с	неопределенными
	m			m	k -					α +iβ как корня
коэффициентами,				а		кратность комплексного		числа

характеристического уравнения однородного уравнения соответствующего

уравнению (2.52)	(если α + iβ	не является	корнем	указанного
характеристического уравнения, то k		считается равным нулю).
Пример 2.11. Найти частное решение уравнения y′′−5 y′+6 = 52 sin 2x .
Правая часть уравнения имеет вид		(2.57), где Pm(2) = 52,	Pm(1) = 0,	α = 0, β = 2 .
Тогда α +βi = 2i , 2i	не является корнем характеристического уравнения, т.е.

k = 0	. Частное решение имеет вид				y	= xk Q(1)	(x)cos 2x +Q(2)	(x)sin 2x	,	где
						m	m
k = 0 , Qm(1) и Qm(2)				просто постоянные (или многочлены нулевой степени).
Итак y = Acos 2x + B sin 2x .
Находим производные y′ = −2 Asin 2x + 2B cos 2x ;							y′′ = −4 Acos 2x − 4B sin 2x			и,
подставляя		y	, y′	y′′ в уравнение, получим:

−4 Acos 2x −4B sin 2x −5(−2 Asin 2x + 2B cos 2x)+6(Acos 2x + B sin 2x)= 52 sin 2x

или

(−4A−10B+6A)cos2x+(−4B+10A+6B)sin2x =(−10B+2A)cos2x+(2B+10A)sin2x =52sin2x.

Приравнивая коэффициенты при cos 2x и sin 2x в правой и левой части,

получим	−10B + 2 A = 0		, откуда	A = 5, B =1	.
	2B +10 A = 52
Таким образом,		y = 5cos 2x + sin 2x .

56

			Решение задач
Задача 2.4. Решить уравнение					y ''−5y '+6 y = (2x −5)e2 x .
Составляем	характеристическое уравнение для						соответствующего
однородного уравнения		λ2	− λ +	6	=	0 и находим его корни	λ = 2,λ	2	= 3.	Так
			5				1
как число α = 2	является простым корнем характеристического уравнения, то

k =1. Степень многочлена m в правой части данного уравнения равна единице, и, следовательно, частное решение следует искать в виде

y = x( Ax + B)e2 x ,

где A и B - неопределенные коэффициенты. Вычислим y ' и y y ' = 2Ax2 +2( A + B)x + B e2x ,

y '' = 4Ax2 +4(2A + B)x +2( A +2B) e2x .

Подставляя y, y ', y '' в данное уравнение и сокращая на e2 x ,

4 Ax2 + 4(2 A + B)x + 2( A + 2B) −10 Ax2 −10( A + B)x

−5B +6 Ax2 +6Bx ≡ 2x −5

или

−2 Ax + 2 A − B ≡ 2x −5.

(2.59)

'' :

получим

−

Приравнивая коэффициенты при одинаковых степенях x , получим систему двух уравнений

	−2 A = 2,
2 A − B = −5,
откуда находим A = −1, B = 3.	Искомое частное решение	имеет вид
y = x(3 − x)e2 x , а общим решением заданного уравнения будет
y = C1e2 x +C2e3x + x(3 − x)e2 x ,		(2.60)
где C1 и C2 - произвольные постоянные.
Задача 2.5. Решить уравнение
y ''+ y '−2 y = ex (cos x −7 sin x).		(2.61)

Составляем характеристическое уравнение для соответствующего

однородного уравнения
λ2 + λ −2 = 0	(2.62)

и находим его корни λ1 =1,λ2 = −2. По виду выражения (2.57) и правой части данного уравнения находим, что α =1,β =1, m = 0. Так как комплексное число α + βi =1 +i не является корнем характеристического уравнения (2.62), то

частное решение уравнения (2.61) в соответствии с равенством (2.58), следует искать в виде

y = x0ex ( Acos x + B sin x),

57

где	A и B - неопределенные коэффициенты, означающие многочлены				Q(1) и
					0
Q(2)	. Вычислим вначале y ' и y '' :
0	y ' = ex (A + B)cos x +(B − A)sin x , y '' = ex (2B cos x −2 Asin x).
	Подставив y, y ', y '' в уравнение (2.61) и сократив на ex , получим
	2B cos x −2Asin x +( A + B) cos x +(B − A) sin x −
или	−2Acos x −2B sin x ≡ cos x −7 sin x.
	(3B − A) cos x +(−3A − B) sin x ≡ cos x −7 sin x.
	Приравнивая коэффициенты при cos x		и sin x ,	получим систему двух
уравнений		3B − A =1,
	−3A − B = −7,
откуда следует A = 2, B =1.		Искомое	частное	решение имеет	вид

y = ex (2 cos x +sin x), а общим решением уравнения (2.61) будет y = C1ex +C2e−2 x +ex (2 cos x +sin x),

где C1 и C2 - произвольные постоянные.

Вопросы для самопроверки по теме 2.3

1.В чем заключается метод Л.Эйлера для построения фундаментальной системы решений линейного однородного уравнения с постоянными коэффициентами?

2.Как найти методом неопределенных коэффициентов частное решение линейного неоднородного уравнения в случаях специального вида правой

части	уравнения:	а)	f (x) = P (x)eax ;	б)
			m

f (x) = eax P(1)		(x) cos βx + P(2)			(x)sin βx	, где	a,α, β	- вещественные числа,
	m			m
P (x), P(1) (x),		P(2)	(x)	- многочлены степени m ?
m	m	m

Раздел 3. Системы обыкновенных дифференциальных уравнений

Данный раздел содержит следующие темы: 3.1.Основные понятия.

3.2.Системы линейных дифференциальных уравнений с постоянными коэффициентами.

3.3. Элементы теории устойчивости.

После изучения теоретического материала следует ответить на вопросы для самопроверки и на вопросы теста №6. При возникающих затруднениях в ответах обратитесь к [1].

58

3.1.Основные понятия

В рассматриваемой теме Вам предстоит познакомиться со следующими вопросами:

•Нормальная система дифференциальных уравнений.

•Метод исключения, фазовое пространство.

Нормальная система дифференциальных уравнений

Ранее мы рассматривали обыкновенные дифференциальные уравнения вида y(n) = f (x, y, y ', y '',..., y(n−1) ),

где x - независимая переменная, y - искомая функция, f - заданная функция

своих аргументов, a n - порядок уравнения.

Однако самые разнообразные задачи науки и техники приводят к необходимости изучения систем дифференциальных уравнений с несколькими неизвестными функциями.

Рассмотрим, например, систему уравнений вида

y '

= f (x, y , y

2

,..., y

n

),

1

1

1

y '2

= f2

(x, y1, y2

,..., yn ),

.....................

(3.1)

y '

n

= f

n

(x, y , y

2

,..., y

n

),

1

где x - независимая переменная, y1, y2 ,..., yn

- неизвестные функции, зависящие

от x a f1, f2 ,...., fn - заданные функции своих аргументов. Система вида (3.1)

называется нормальной системой дифференциальных уравнений.

Можно показать, что любая система уравнений, разрешенных относительно старших производных искомых функций может быть приведена к нормальной системе вида (3.1).

Всякая совокупность функций y1(x), y2 (x),..., yn (x) определенных и непрерывно дифференцируемых на интервале (a, b) называется решением системы (3.1) в этом интервале, если при подстановке их в уравнения системы они обращают их в тождества, справедливые при всех x из (a, b) . Процесс

нахождения решений системы (3.1) называется интегрированием (решением)

этой системы.

Метод исключения, фазовое пространство

Можно показать, что при выполнении довольно общих условий, система уравнений (3.1) может быть сведена к одному дифференциальному уравнению

n -го порядка относительно любой из функций y1, y2 ,..., yn или к группе

уравнений (с одной неизвестной функцией каждое), сумма порядков которых равна n .

59

Достигается это с помощью метода исключения, который состоит в том, что из системы (3.1) при помощи последовательного (n −1) - кратного

дифференцирования, например функции y '1 , и замены y1′, y2′,..., yn′ каждый раз их значениями из системы (3.1), получают систему из n уравнений, из которой, исключая y2 , y3 ,..., yn , получают одно уравнение n -го порядка относительно функции y1 (случай получения группы уравнений не приносит ничего

принципиально нового). Найдя общее решение этого уравнения, определяют остальные функции без квадратур.

Если независимую переменную x трактовать как время и ввести в

рассмотрение n -мерное пространство с координатами y1, y2 ,..., yn , назвав его

фазовым, то всякое решение системы (3.1) представляет собой движение точки в фазовом пространстве. Поэтому решению системы (3.1) соответствует движение точки в фазовом пространстве, а кривая, описываемая в нем движущейся точкой, называется траекторией этого движения. Начальная задача, или задача Коши для нормальной системы (3.1) ставится так: найти решение системы (3.1), которое удовлетворяло бы начальным условиям

y1(x0 ) = y10 , y2 (x0 ) = y20 ,..., yn (x0 ) = yn0 ,	(3.2)
где x0 , y10 , y20 ,..., yn0 - заданные числа.
Если ввести в рассмотрение вектор Y с координатами	y1(x), y2 (x),..., yn (x),

то система (3.1) и начальные условия (3.2) могут быть записаны в векторном виде

dY	= F(x,Y ), Y (x ) =Y ,
dt	0	0

где F - векторная функция с координатами ( f1, f2 ,..., fn ), а Y0 - n -мерный вектор с координатами (y10 , y20 ,..., yn0 ).

Как и ранее, возникает вопрос о существовании и единственности решения системы (3.1), удовлетворяющей начальным условиям (3.2).

Оказывается, что теорема существования и единственности решения для уравнения первого порядка в нормальной форме распространяется и на нормальную систему уравнений.

Теорема 3.1. Если правые части системы (3.1) непрерывны в некоторой окрестности точки (x0 , y10 , y20 ,..., yn0 ) и имеют в этой окрестности непрерывные частные производные по y1, y2 ,..., yn , то система (3.1) имеет единственное решение y1(x), y2 (x),..., yn (x), определенное в некоторой окрестности точки x0

и удовлетворяющее начальным условиям (3.2).

По аналогии с введенными для дифференциального уравнения n -го порядка понятиями общего и частного решений, вводятся понятия общего и частного решений системы уравнений (3.1).

Продемонстрируем применение метода исключения.

60

Пример 3.1. Решить систему уравнений

y ' = z +u,
	(3.3)
z ' = 3y +u,
u ' = 3y + z.

Получим дифференциальное уравнение для определения функции u(x) . С

этой целью продифференцируем третье уравнение системы (3.3) u '' = 3y '+ z '

и заменим производные y ', z ' через их выражения из системы (3.3):

u '' = 3(z +u) +3y +u = 3y +3z + 4u.

(3.4)

Выпишем систему уравнений, состоящую из уравнения (3.4) и третьего уравнения системы (3.3)

				u ' = 3y + z,
		u ''−4u = 3y +3z.
Разрешив ее относительно y и z,			получим
y = −	1	u ''+	1	u '+	2	u, z =	1	u ''−	1	u '−2u.	(3.5)
			2		3		2		2
6
Продифференцируем теперь уравнение (3.4)
		u ''' = 3y '+3z '+ 4u '
и заменим производные y′ и z ' через их выражения из системы (3.3):
u ''' = 3(z +u) +3(3y +u) + 4u ' = 4u '+9 y +3z +6u.											(3.6)

Подставив теперь в правую часть (3.6) вместо y и z, соответствующие выражения из (3.5), получим

u ''' = 4u '+6u − 32 u ''+ 92 u '+6u + 23 u ''− 32 u '−6u

или

u '''−7u '−6u = 0.

Получено линейное однородное дифференциальное уравнение третьего порядка с постоянными коэффициентами. Составим его характеристическое

уравнение λ3 −7λ −6 = 0 и найдем корни λ1 = −1, λ2 = −2,			λ3 = 3. Это значит,
что для u(x) можно записать
u(x) = C1e−x +C2e−2 x +C3e3x ,			(3.7)
где C1,C2 ,C3 - произвольные постоянные. Подставив выражение (3.7) в (3.5),
найдем
y(x) = −C2e−2 x +	2	C3e3x ,	(3.8)
3
z(x) = −C1e−x +C2e−2 x +C3e3x .			(3.9)

Совокупность выражений (3.7), (3.8) и (3.9) образует общее решение системы (3.3).

61

3.2.Системы линейных дифференциальных уравнений

спостоянными коэффициентами

Врассматриваемой теме Вам предстоит ознакомиться со следующими вопросами:

•Линейные однородные и линейные неоднородные системы.

•Характеристическое уравнение системы.

При необходимости дополнительной информации обращайтесь к [1].

Линейные однородные и линейные неоднородные системы

Важное значение среди нормальных систем дифференциальных уравнений имеют системы вида

y '

= a

(x) y

+a

(x) y

2

+... +a

(x) y

n

+ f (x),

1

11

1

12

1n

1

y '2

= a21

(x) y1 +a22

(x) y2

+... +a2n (x) yn + f2

(x),

.........................................

(3.10)

y '

= a

(x) y + a

(x) y

2

+... + a

(x) y

n

+ f

n

(x),

n

n1

1

n2

nn

где функции aij (x)(i, j =1, 2,..., n) и fi (x)(i =1, 2,..., n) непрерывны на некотором интервале (a, b) . На основании теоремы существования и единственности решения нормальной системы можно утверждать, что для любого значения x0

из (a, b) и любых чисел y10 , y20 ,..., yn0 у системы (3.10) существует единственное решение y1(x), y2 (x),..., yn (x), которое определено в некоторой окрестности точки x0 и удовлетворяет начальным условиям

y1(x0 ) = y10 , y2 (x0 ) = y20 ,..., yn (x0 ) = yn0 .

Если на интервале (a, b) функции f1(x), f2 (x),..., fn (x) тождественно равны

нулю, то система (3.10) называется линейной однородной; в противном случае

- линейной неоднородной.

Теория линейных систем (свойства их решений, структура общего решения, специальные методы интегрирования) аналогична теории линейных дифференциальных уравнений n -го порядка.

Характеристическое уравнение системы

Рассмотрим подробнее системы линейных однородных дифференциальных уравнений с постоянными коэффициентами. Для простоты записи ограничимся случаем n = 3.

Итак, рассмотрим систему

62

где

где

y '		= a	y	+ a	y	2
	1	11	1	12
y '2 = a21 y1 + a22 y2
y '		= a	y	+ a	y	2
	3	31	1	32

aij (x)(i, j =1, 2,..., n) - вещественные числа.

+ a13 y3 ,
+ a23 y3 ,	(3.11)
+ a33 y3 ,

Используя метод Эйлера, будем искать решение системы (3.11) в виде

y	= γ eλx , y	2	= γ	2	eλx , y	= γ eλx ,	(3.12)
1	1				3	3

λ, γ1, γ2 , γ3 - некоторые числа, которые надо подобрать так, чтобы функции

(3.12) были бы решением системы (3.11).

Подставив функции (3.12) в систему (3.11), получим (после сокращения на eλx и переноса всех членов в левую часть равенств):

	(a − λ)γ + a γ							2	+ a γ	3		= 0,
	11		1			12			13
a21γ1 + (a22 − λ)γ2 + a23γ3												= 0,	(3.13)
a		γ + a γ		2	+ (a				− λ)γ		3	= 0.
	31	1	32					33
Эта система уравнений служит для определения неизвестных													γ1, γ2 , γ3,λ.
Относительно γ1, γ2 , γ3			система				(3.13)				является системой		линейных

однородных уравнений. Известно, что для того чтобы система линейных однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы ее определитель был равен нулю, т.е. число λ должно удовлетворять уравнению

a11 − λ	a12	a13
a21	a22 − λ	a23		= 0.	(3.14)
a31	a32	a33 − λ

Уравнение (3.14) называется характеристическим (вековым) уравнением системы (3.11), а его корни - характеристическими числами системы (3.11).

В нашем случае уравнение (3.14) - уравнение третьей степени относительно λ. Рассмотрим случай, когда все корни λ1,λ2 ,λ3 характеристического уравнения вещественны и различны. Подставляя поочередно каждый корень

λi (i =1,2,3) вместо λ в систему (3.13) и находя каждый раз ненулевые решения

γi1, γi2 , γi3 , сможем получить три частных решения системы (3.11):

γi1eλi x , γi2eλi x , γi3eλi x (i =1,2,3).

(3.15)

Можно показать, что линейная комбинация решений (3.15) с произвольными постоянными C1,C2 ,C3 представляет собою общее решение системы (3.11)

63

y

= C

γ

eλ1x

+C

γ

eλ2 x + C

γ

eλ3 x ,

1

1

11

2

21

3

31

= C1γ12eλ1x +C2γ22eλ2 x +C3γ32eλ3 x ,

y2

y

= C

γ

eλ1x

+C

γ

eλ2 x +C

γ

33

eλ3 x.

3

1

13

2

23

3

Пример 3.2. Найти частное решение системы уравнений

y ' = y −2z −u,

= −y

+ z +u,

(3.16)

z '

= y −u,

u '

удовлетворяющее начальным условиям

y(0) = 7,

z(0) = 0,

u(0) =1.

(3.17)

Вначале обратим внимание на то, что искомые функции в каждом из уравнений системы (3.16) следуют друг за другом в том же порядке, в котором выписаны уравнения, разрешенные относительно y ', z ', u '.

Найдем сначала общее решение системы (3.16), для чего составим ее характеристическое уравнение

	1 − λ	−2	−1
	−1	1 − λ	1	= 0.
	1	0	−1 − λ
Раскрыв определитель, стоящий в левой части, будем иметь
(λ −1)(1 −λ2 ) − 2 +1 −λ + 2(1 + λ) = 0				или λ3 −λ2 − 2λ = 0.
Записав последнее уравнение		в виде λ(λ2 −λ − 2) = 0, легко найти его

корни, т.е. характеристические числа системы (3.16)

λ1 = 0, λ2 = 2, λ3 = −1.

Построим частное решение вида (3.12), соответствующее корню λ1 = 0, для

чего подставим в систему (3.13)	λ1 = 0. Получим
	γ	− 2γ	2	− γ		3	= 0,
	1
−γ1 + γ2 + γ3 = 0,
		γ − γ		3	= 0.
		1

Поскольку достаточно найти одно ненулевое решение этой системы, то, положив γ3 =1, найдем γ1 =1, γ2 = 0. Подставляя найденные значения в (3.12), получим первое частное решение системы (3.16)

y =1, z = 0, u =1.

(3.18)

Построим частное решение вида (3.12), соответствующее корню λ2 = 2, для

чего подставим в систему (3.13)	λ2 = 2. Получим:
−γ		− 2γ	2	− γ		3	= 0,
	1
	−γ1 − γ2 + γ3 = 0,
	γ −3γ			3	= 0.
		1
		64

Для отыскания одного ненулевого решения этой системы положим γ3 =1.

Тогда найдем γ1 = 3, γ2 = −2. Используя	формулы	(3.12), получим второе
частное решение
y = 3e2 x , z = −2e2 x ,	u = e2 x .	(3.19)

Для получения третьего частного решения вида (3.12), отвечающего корню λ3 = −1, положим в системе (3.13) λ = −1. Будем иметь

2γ1 − 2γ2 − γ3 = 0,−γ1 + 2γ2 + γ3 = 0,

γ = 0.

1

Из третьего уравнения следует γ1 = 0, а чтобы найти ненулевое решение последней системы, положим γ2 =1, тогда из первого (или второго) уравнения следует γ3 = −2. Подставляя найденные значения в (3.12), получим третье частное решение системы (3.16)

y = 0, z = e−x , u = −2e−x .

(3.20)

Используя частные решения (3.18),(3.19),(3.20), выпишем общее решение системы (3.16)

	y = C1 +3C2e2 x ,
	z = −2C2e2 x +C3e−x ,		(3.21)
u = C +C e2 x −2C e−x ,
	1 2	3

где C1,C2 ,C3 - произвольные постоянные.

Для получения частного решения, удовлетворяющего начальным условиям (3.17), положим в равенствах (3.21) x = 0 и воспользуемся условиями (3.17).

Получим систему уравнений для определения значений C1,C2 ,C3 .

	C + 3C		= 7,
	1	2
	−2C2 + C3 = 0,
C1 +C2 − 2C3 =1.
Решив последнюю систему,	найдем		C1 = 4,C2 =1,C3 = 2, а тогда частное
решение имеет вид
	y = 4 +3e2 x ,

z = −2e2 x + 2e−x ,

u = 4 + e2 x − 4e−x.

Решение задач

Задача 3.1. Проверить, является ли совокупность двух функций

65

	y(x) =	C1	,	z(x) =						C2	(3.22)
										x2
		x				y
	y′ = −							,
общим решением системы						x					(3.23)
					2z
	z′ = −					x

в интервале 0 < x < ∞ и, если является,		найти частное	решение,
удовлетворяющее начальным условиям y(1) = 2,	z(1) = 3 .
Функции (3.22) разрешимы относительно C1	и	C2 и при любых	C1 и C2

должны при подстановке их в систему (3.23) обратить каждое уравнение

системы

в

тождество

для

любого

x > 0 .

Найдем

производные

C1

′

C1

C2

′

−2C2

y′ =

= −

;

z′ =

= C2 (−2)x−3 =

,

подставим

их

в систему

x

x2

x2

x3

−C1

2C2

(3.23). В левых частях уравнений получим выражения

и −

, в правых

y

C

C

x2

x3

1

2z

C

2

1

2C

2

частях уравнений получим

−

= −

1

= −

1

и

−

= −2

= −

. В

x

x

x2

x

x

x

x2

x3

итоге имеем

−C1

= −C1 и −

2C2

= −

2C2

. Итак, система функций (3.22) – общее

x3

x3

x2

x2

решение системы (3.23).

Найдем частное решение, удовлетворяющее начальным условиям, для этого

подставим x =1,

y = 2,

z = 3 в (3.22) для определения

C1 и C2

2 =

C1

,

3 =

C2

,

откуда

C1 = 2, C2 = 3

и

y = 2 , z =

3

- частное

решение

2

2

1

1

x

x

системы (3.23), удовлетворяющее начальным условиям.

dy

= 2 y −2z,

Задача 3.2. Найти решение системы

,

(3.24)

dx

dz

= 7 y −13z

удовлетворяющее начальным условиям

dx

y(0) = −1,

z(0) = 6 .

(3.25)

Дана линейная система двух обыкновенных дифференциальных уравнений с постоянными коэффициентами. Используем метод Эйлера для ее решения. Ищем решение системы (3.24) в виде

			y = γ1eλx ,			z = γ2eλx .					(3.26)
Подставим (3.26) в систему (3.24), получим
	λγ1e			λx	= 2γ1e	λx	− 2γ2e			λx	,
			eλx = 7γ eλx −13γ						eλx.
λγ		2						2
					1
					66

После сокращения на eλx и переноса всех членов в левую часть равенств, получим

γ1(2 −λ) − 2γ2 = 0,					(3.27)
7	γ + (−13	−λ)γ	2	= 0.
	1

Получили однородную систему алгебраических уравнений относительно γ1 и γ2 , которая имеет ненулевые решения, если определитель равен нулю, т.е.

	2 −	λ	−2		= 0. Это уравнение	является	характеристическим уравнением
	7	−13 − λ
системы.			Раскрывая определитель,			имеем	(2 −λ)(−13 −λ)−7 (−2) = 0, или

λ2 +11λ −12 = 0. Это квадратное уравнение имеет два вещественных различных корня λ1 =1 и λ2 = −12 .

Построим частное решение вида (3.26) для первого корня

характеристического уравнения

λ1 =1, т.е.

y1 = γ11e1x

и z2 = γ21e1x . Запишем

систему (3.27) для λ1 =1. Получим

γ

(

2 −1 − 2γ

21

= 0

γ =

2

γ

21

11

)

11

.

+ (−13 −1)γ21 = 0

=14γ21

7γ11

7γ11

	Чтобы получить первое ненулевое решение, положим γ11 = 2, γ21 =1, тогда
y	= 2ex , z	2	=1ex	- первое частное решение.
1

Построим второе частное решение вида (3.26) для				λ2 = −12 . Запишем для
λ2 = −12 , систему (3.27):
γ12 (2 −(−12))− 2γ22 = 0,			14γ12 = 2γ22 ,
	+(−13 −(−12))γ22	= 0		= γ22	,
γ12 7			+7γ12

тогда возьмем		γ12 =1, γ22 = 7 и		получим					второе частное решение
y2 =1 e−12 x ,	z2 = 7 e−12 x . Общее решение системы линейных уравнений (3.24)
запишется	в виде линейной		комбинации					частных		решений, т.е. в виде
y = C1 y1 +C2 y2 ,		z = C1z1 +C2 z2 .	Для	нашей				системы		имеем искомое общее
решение
		y = C 2ex +C					e−12 x ,
			1			2			.	(3.28)
						7e−12 x
		z = C ex +C			2
			1

Чтобы найти частное решение, удовлетворяющее начальным условиям

(3.25), подставим в (3.28)			x = 0,	y = −1, z = 6 .
Получим систему	2C +C = −1,				решая ее, найдем	C1 = −1, C2 =1, тогда
		1	2
	C1	+7C2 = 6,

искомое частное решение:

67

	x	+e	−12 x	,
y = −2e
	+7e−12 x .
z = −ex

Задача 3.3. Найти решение системы дифференциальных уравнений методом

исключения	y′ = 2 y + 2z,		(3.29)
		+3z.
	z′ = y

Метод исключения заключается в сведении системы дифференциальных уравнений к одному дифференциальному уравнению. В данном случае система второго порядка и получить нужно уравнение второго порядка. Для этого продифференцируем второе уравнение

z′′ = y′+3z′

(3.30).

Подставим в (3.30) y′ = 2 y + 2z , получим z′′ = 2 y + 2z +3z′, куда подставим из второго уравнения y = z′−3z , тогда z′′ = 2 (z′−3z)+ 2z +3z′, т.е. z′′−5z′+ 4z = 0 . Получили линейное уравнение второго порядка с постоянными

коэффициентами.

Его

характеристическое

уравнениеλ2 −5λ + 4 = 0 имеет

корни λ1 =1, λ2 = 4.

Корни

вещественные

различные.

Общее решение

уравнения

z′′−5z′+ 4z = 0 имеет вид z = C1eλ1x +C2eλ2 x , т.е.

z = C1ex +C2e4 x .

Выражение для y

найдем из

второго

уравнения

системы,

где y =

dz

−3z .

dx

Учитывая,

что z = C1ex +C2e4 x ,

получим

y = C1ex +4C2e4x −3

(C1ex +C2e4x )

или

y = −2C ex

+C e4 x .

1

2

y = −2C ex +C

e4 x ,

Общее решение системы (3.29):

1

2

e4 x .

z = C ex +C

1

2

Вопросы для самопроверки по теме 3.2

1.Как записать в общем виде нормальную систему дифференциальных уравнений n -го порядка?

2.Что называется решением системы обыкновенных дифференциальных уравнений?

3.В чем заключается метод исключения?

4.Как ставится задача Коши для нормальной системы дифференциальных уравнений n -го порядка?

5.Какая система дифференциальных уравнений называется линейной?

6.Какая система дифференциальных уравнений называется однородной, неоднородной?

7.Как записать характеристическое уравнение линейной однородной системы?

8.Как записать общее решение линейной однородной системы?

68

3.3. Элементы теории устойчивости

Основные вопросы теории устойчивости по Ляпунову изложены в [1], стр. 57-65. После изучения данного материала необходимо ответить на вопросы для самопроверки.

Вопросы для самопроверки по теме 3.3

1.Какое движение называтся возмущенным, какое – невозмущенным. В чем их различие?

2.Какая плоскость называется фазовой?

3.Что называется вариациями величин?

4.Дайте определение устойчивого по Ляпунову невозмущенного движения.

5.При каком условии решение устойчивое по Ляпунову будет асимптотически устойчивым?

6.Выпишите систему уравнений возмущенного движения.

7.Какя динамическая система называется автономной.

8.Что называется положением равновесия или точкой покоя автономной системы?

9.Разница между понятиями устойчивого и неустойчивого узла заключается в …….

10.Седлом называется………….

11.Определите понятия устойчивого и неустойчивого фокусов.

12.От чего зависит устойчивость нулевого решения линейной системы двух уравнений с постоянными коэффициентами?

13.Сформулируйте основные теоремы об устойчивости, асимптотической устойчивости и неустойчивости.

14.Функциями Ляпунова называют……..

15.Предельным циклом системы дифференциальных уравнений называется…

Раздел 4. Основы вариационного исчисления и оптимального управления

Данный раздел содержит следующие темы:

4.1.Основы вариационного исчисления.

4.2.Основы оптимального управления.

После изучения теоретического материала следует ответить на вопросы для самопроверки и на вопросы теста №7. При возникающих затруднениях в ответах обратитесь к [1].

69

4.1. Основы вариационного исчисления

Теоретический материал изложен в [1], стр. 65-74. Вам необходимо ознакомиться с основными понятиями и задачами данной темы, вывести уравнение Эйлера и рассмотреть частные случаи его решения; решить задачу о брахистохроне. После изучения материала следует ответить на вопросы для самопроверки.

Вопросы для самопроверки по теме 4.1

1.Дайте определение функционала.

2.Основной задачей вариационного исчисления является….

3.Какую вариационную задачу называют простейшей.

4.Сильной окрестностью функции называется…..

5.Абсолютный экстремум – это…….

6.В чем разница между сильным и слабым минимумом функционала.

7.Выпишите уравнение Эйлера.

8.Какому необходимому условию должна удовлетворять функция y (x), чтобы достигался экстремум функционала V .

9.Что такое экстремали задачи.

10..Брахистохроном называется….

4.2. Основы оптимального управления

Теоретический материал изложен в [1], стр. 75-80. В рассматриваемой теме Вам предстоит ознакомиться с основныеми понятия теории оптимального управления, принципом максимума Понтрягина. После изучения материала следует ответить на вопросы для самопроверки.

Вопросы для самопроверки по теме 4.2

1.Что называется фазовым пространством системы.

2.Областью управления называется…..

3.Управление называется допустимым на отрезке, если……

4.Множество достижимости – это……

5.Какая функция называется функцией Гамильтона.

6.Сформулируйте принцип максимума Понтрягина.

7.Приведите примеры задач по определению оптимального управления.

70