Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный минерально-сырьевой университет «Горный»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

matematika.pdf

Скачиваний:

Добавлен:

02.04.2015

Размер:

1.89 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 137 8 9 10 11 12 13 > Следующая >>>

Раздел 5. Числовые и функциональные ряды

Продолжаем изучение курса математики, рассматривая числовые и функциональные ряды, которые находят широкое применение при решении практических задач в различных областях науки и техники.

Данный раздел включает следующие темы:

•5.1. Числовые ряды.

•5.2. Функциональные ряды.

По каждой теме излагается основной теоретический материал, и приводятся иллюстрирующие его примеры. В конце каждой темы подробно разобраны типовые задачи.

Студентам очно-заочной и заочной форм обучения надо решить две задачи из контрольных работ № 5 и № 6.

5.1. Числовые ряды

При изучении данной темы Вам предстоит познакомиться со следующими вопросами:

•Числовые ряды и их простейшие свойства.

•Числовые неотрицательные ряды. Признаки сравнения.

•Признаки Коши и Даламбера сходимости положительных числовых рядов.

•Знакопеременные ряды. Знакочередующиеся ряды.

После изучения теоретического материала следует ответить на вопросы для самопроверки и на вопросы теста №8. При возникающих затруднениях в ответах обратитесь к [2].

Студентам очно-заочной и заочной форм обучения надо решить одну задачу из контрольной работы № 5 под номерами 31-40 в соответствии со своим вариантом.

Числовые ряды и их простейшие свойства

Рассмотрим понятие числового ряда. Пусть дана бесконечная последовательность чисел a1, a2 ,..., an ,..., которые могут быть как

вещественными, так и комплексными. Символ
a1 + a2 +... + an +...	(5.1)
называют числовым рядом, а члены последовательности	a1, a2 ,..., an ,..., -

∞

членами ряда. Для обозначения ряда применяют также запись ∑ an , где an

n=1

называют общим членом ряда.

Замечание. Последовательности чисел a0 , a1, a2 ,..., an ,..., соответствует

ряд

∞

a0 +a1 +a2 +a3 +... +an +... = ∑ an.

Например, таким рядом будет

n=0

∞

1+1+

+... +

+... = ∑

.Если последовательность чисел имеет

n=0 n!

вид am , am +1, am +2 ,..., am +n ,...,

то соответствующий ей ряд запишется в виде

am +am+1 +am+2 +

∞

... +am+n +... = ∑ ak .

k =m

Сам по себе символ (5.1) никакого определенного смысла не имеет, потому что действие сложения в своем непосредственном содержании имеет дело каждый раз лишь с конечным числом слагаемых, т.е. смысл выражению (5.1) предстоит приписать нам самим. Формулировки различных определений числового ряда и сопоставление их друг с другом представляют большой интерес как теоретический, так и практический. Однако мы сейчас ограничимся рассмотрением лишь одной такой формулировки.

Определение 5.1. Сумма Sn = a1 + a2 +... + an						первых	n членов ряда
(5.1) называется n - й частичной суммой этого ряда.
Ряд (5.1) называется сходящимся, если последовательность его
частичных сумм S , S		2	,..., S	n	,... имеет конечный предел lim S		n	= S.
	1	2		n		n→∞	n
Значение S этого предела называется суммой ряда (5.1). В этом случае
	∞				∞
пишут	∑an = S.		Тем самым символу ∑an			придается определенный
	n=1				n=1

числовой смысл.

Определение 5.2. Ряд (5.1) называется расходящимся, если последовательность его частичных сумм не имеет конечного предела.

Содержание теории числовых рядов состоит в установлении сходимости или расходимости тех или иных рядов и в вычислении сумм сходящихся рядов. Простейшим примером числового ряда является геометрический ряд

a + aq + aq2 + ... + aqn −1 + ...,					(5.2)
члены которого образуют известную нам геометрическую			прогрессию.
Исследуем геометрический ряд на сходимость.
С этой целью рассмотрим частичную сумму
	Sn	= a + aq + ... + aqn −1			(5.3)
и изучим ее поведение	при	n →∞. Очевидно, что поведение		S n	будет
зависеть от значения q.
Пусть q ≠1, тогда,	умножая обе части равенства (5.3) на		q	и вычитая
полученное равенство из (5.3), мы будем иметь Sn (1 − q) = a − aqn .					Откуда
следует		72
		72

−

qn .

(5.4)

− q

1 − q

Очевидно, что поведение

S n

при

n→∞ определяется поведением второго

слагаемого, содержащего qn .

Известно,

что если | q |<1, то qn → 0 при n → ∞,

и, значит, частичная

сумма ряда

S n

будет

стремиться

при

n →∞.

Поэтому

1 − q

геометрический ряд при | q |<1 сходится, и его сумма S =

так что мы

− q

можем написать

a + aq + aq 2

+ ... + aq n −1 + ... =

(| q |< 1).

При | q |>1,

− q

величина q n

в равенстве (5.4)

не имеет конечного предела при

n → ∞, и, следовательно, при | q |>1 геометрический ряд расходится.

Если

q =1,

то

частичная

сумма

равна

Sn = na,

и,

значит,

геометрический ряд при q =1 расходится, так как lim S

=∞.

n→∞

Остается рассмотреть q =−1. В этом случае мы получаем ряд

a − a + a − a + ...

Частичная сумма S n равна нулю,

если n - четное,

и равна a ,

если n -

нечетное, таким образом,

S n

не имеет предела,

и поэтому при

q =−1 ряд

расходится.

Итак, геометрический ряд (5.2) сходится только при | q |<1.

Пример 5.1. Исследовать на сходимость ряд

+... = ∑

1 .

1 +

+ 1

+... +

∞

1 2 2 3 3 4

n(n +1)

n =1 n(n +1)

Решение. Найдем его частичную сумму Sn . Имеем

1 .

Sn =

1 +

+ 1

+... +

= ∑

1 2 2 3 3 4

n(n +1) k =1 k(k +1)

Эту частичную сумму можно упростить, если заметить, что

−

k(k +1)

k +1

Итак, для частичной суммы получим

Sn = 1

−

... +

−

n +

Очевидно, что Sn → 1 при	n →∞. Следовательно, заданный ряд
сходится, и его сумма S равна 1, так что мы можем написать
∑	1 =1.
∞

n=1 n(n +1)

Пример 5.2. Исследовать на сходимость ряд

∞

∑ ln 1 +

n=1

Решение. Найдем частичную сумму этого ряда. Имеем

k +1

Sn = ∑ ln 1

∑ ln

∑ (ln(k +1)

− ln k ) =

k =1

= (ln 2 − ln1) + (ln 3 − ln 2) +... + (ln(n +1) − ln n) = ln(n +1)

или

S n = ln(n + 1).

Так как

→ +∞

при

n → +∞,

то заданный ряд расходится. При этом мы можем написать

∞

∑ln 1

= +∞.

n=1

Сходящиеся числовые ряды обладают некоторыми свойствами, которые позволяют действовать с ними, как с конечными суммами.

Свойства сходящихся числовых рядов

1) Если ряд (5.1) сходится и имеет сумму S , то ряд

αa1 +αa2 +... +αan +...

также сходится и его сумма равна αS .

2) Сходящиеся ряды можно почленно складывать и вычитать, т.е. если

		∞				∞
		∑αn = A и				∑βn = B,
		n=1				n=1
∞	(αn −βn )	∞	(αn +βn )
то ряды ∑	(αn −βn )	и ∑	(αn +βn )		также сходятся, и их суммы равны
n=1		n=1
соответственно A −B и A + B . Это утверждение можно записать в виде такого
равенства		∞	∞		∞
		∞	∞		∞	(αn ±βn ).
		∑αn ± ∑βn		=∑		(αn ±βn ).
		n=1	n=1		n=1

3) Свойство сходимости или расходимости ряда не нарушается, если у ряда отбросить или приписать к нему любое конечное число членов с начала.

4) (Необходимый признак сходимости ряда). Общий член an

сходящегося ряда стремится к нулю при n →∞.

Пример 5.3. Покажем, что ряд

∞

2n−1 +1

∑

+... +

+...

n=1

расходится.

Решение. Действительно, для этого ряда

lim an = lim

2n −1 +1

= lim

≠ 0,

n →∞

т.е. необходимый признак сходимости ряда не выполняется, следовательно, ряд расходится.

Подчеркнем, что необходимый признак сходимости является необходимым, но не достаточным. В дальнейшем мы познакомимся с

многочисленными рядами, для которых lim a								= 0, но которые, тем не менее,
					n→∞ n
расходятся. Здесь же приведем в качестве примера ряд
	1		1		1			∞	1
1+		+		+... +		+...	= ∑			,
	2		3		n
								n=1 n

который называется гармоническим рядом, и который расходится, в чем мы

убедимся чуть позднее, хотя общий член этого ряда стремится к нулю при

n→∞.

Числовые неотрицательные ряды. Признаки сравнения

∞

Рассмотрим ряд ∑ an , все члены которого неотрицательны, так что

n=1

an ≥ 0. Такой ряд носит название неотрицательного.

Во многих задачах, теоретических и практических, необходимо установить лишь сам факт сходимости или расходимости числового ряда. Например, сходимость ряда можно установить, составив последовательность его частичных сумм и выяснив, имеет ли эта последовательность конечный предел. Этот признак является, очевидно, необходимым и достаточным признаком сходимости рядов. Стремление к нулю общего члена ряда по мере роста его номера также является признаком сходимости ряда, однако только

Каждый член гармонического ряда, начиная со второго, является средним гармоническим двух соседних с ним членов. Средним гармоническим двух чисел a и b называется число

c =		2		.
	1	+	1

	a		b	75

необходимым, но не достаточным.

В дальнейшем будем рассматривать ряды, у которых общий член положителен, т.е. an > 0. Такие ряды называют положительными.

Необходимый и достаточный признак сходимости положительного ряда дает следующая теорема.

∞

Теорема 5.1. Для того чтобы положительный ряд ∑an сходился,

n=1

необходимо и достаточно, чтобы его частичные суммы S n были ограничены сверху Sn ≤ M (M = Const, n =1, 2,...).

Приведенная теорема является основной теоремой теории положительных рядов. Этой теоремой можно воспользоваться при доказательстве расходимости гармонического ряда. Именно неограниченность частичных сумм гармонического ряда и является причиной его расходимости.

Указанная теорема о необходимом и достаточном условии сходимости положительного ряда на практике применяется редко, так как она требует нахождения оценки частичной суммы ряда, что удается сделать лишь в редких случаях. Желательно иметь в своем распоряжении признаки сходимости, основанные на оценках только общего члена ряда. При этом естественно возникает вопрос, нельзя ли, зная поведение одного ряда, судить о поведении другого ряда путем сравнения их общих членов. Оказывается, можно. Соответствующие признаки сходимости (расходимости) называются

признаками сравнения.
Теорема 5.2. (Первый признак сравнения). Пусть даны два
положительных ряда
a1 + a2 +... + an +...	(5.5)
и
b1 + b2 +... + bn +...,	(5.6)

причем члены первого ряда, начиная с некоторого номера k,не превосходят соответствующих членов второго ряда:

an < bn , n = k, k +1,... .

Тогда из сходимости ряда (5.6) следует сходимость ряда (5.5), а из расходимости ряда (5.5) следует расходимость ряда (5.6).

Пример 5.4. Исследовать сходимость ряда

∞	1			1			1		1
∑			=1+			+		+... +			+...	(5.7)
		2		2	2		2		n	2
n=1 n							3

Решение. Сравним данный ряд с рядом:

1 + ∑ 1	=1 + 1 + 1 +... +	1 +...,	(5.8)
∞
n =1 n(n +1)	1 2 2 3	n(n +1)

который сходится (см. пример 5.1). Имеем:

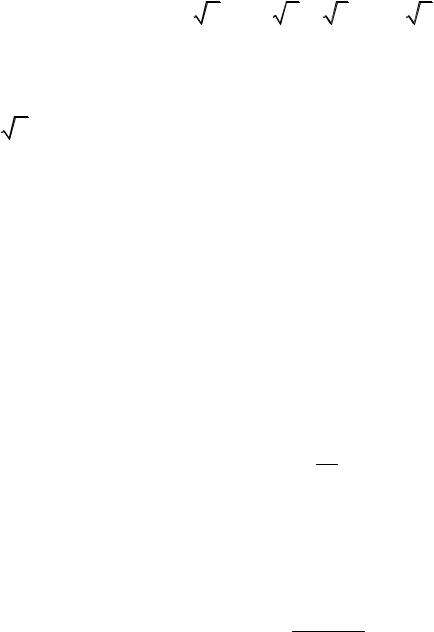
1	=			1			<		1	, т.е.
(n +1)2			(n +1)(n +1)					n(n +1)

		1			<		1		.	(5.9)
		(n +		1)2		n(n +1)

Так как ряд (5.8) сходится, то, учитывая неравенство (5.9), согласно первому признаку сравнения, сходится и ряд (5.7).

Во многих случаях в качестве рядов сравнения берут геометрический или гармонический ряды.

Пример 5.5. Исследовать на сходимость ряд

∞

∑

=1 +

+... +

+...

n =1

∞

Решение. Сравним этот ряд с гармоническим рядом

∑

. Имеем

n=1 n

(n ≥ 2). Но гармонический ряд расходится.

Следовательно, по

первому признаку сравнения, заданный ряд тоже расходится.

Теорема 5.3. (Второй признак сравнения). Пусть даны два положительных ряда (5.5) и (5.6), причем можно указать такие постоянные

m > 0 и M >0, что, начиная с некоторого n , выполняются неравенства

m ≤	an	≤ M .
m ≤	b	≤ M .
	b
	n
Тогда ряды (5.5) и (5.6) одновременно сходятся или одновременно
расходятся.			an
Следствие. Если для рядов (5.5)		и (5.6) отношение	an	стремится к
Следствие. Если для рядов (5.5)		и (5.6) отношение	b	стремится к
			b
			n

некоторому конечному положительному пределу

lim an = l > 0,

n→∞ bn

то указанные ряды сходятся или расходятся одновременно. Это следствие более удобно для практического применения чем непосредственное использование второго признака сравнения.

Пример 5.6. Исследовать сходимость ряда

∞ 1

n∑=1 4 5n −3.

∞ 1

Решение. Сравним исходный ряд с рядом ∑ n , общий член которого

n=1 5

равен bn = 51n и является членом геометрической прогрессии со знаменателем

q = 15 . Чтобы воспользоваться вторым признаком сравнения, вычислим

предел:

lim

= lim

Так как найденный предел

n→∞ bn

→∞ 4 5n −3

n→∞ 4 −

∞

конечен

и отличен от

нуля, а

ряд сравнения

∑

сходится,

то,

согласно

n=1

второму признаку сравнения, сходится и данный ряд.

Пример 5.7. Исследовать сходимость ряда

∞

∑

n(n +1)

n =1

∞

Решение. Сравним исходный ряд с гармоническим рядом

∑

общий

n=1 n

член которого b

lim

= lim

n(n +1)

= lim

= 1.

n → ∞ bn

n → ∞

n(n +1)

n → ∞

Так как предел конечен и отличен от нуля, и гармонический ряд расходится, то, согласно второму признаку сравнения, данный ряд расходится.

Признаки Коши и Даламбера сходимости положительных числовых рядов

Продолжим изучение признаков сходимости положительных числовых рядов. Пусть дан ряд

a1 + a2 +... + an +...,

(5.10)

члены которого положительны и не возрастают a1 ≥ a2 ≥... ≥ an ≥ ... .

И пусть введена функция f (x), определенная для всех x ≥1,

непрерывная, невозрастающая и такая, что

f (1) = a1, f (2) = a2 ,..., f (n) = an ,... .

Имеет место следующая теорема:

Теорема 5.4. (Интегральный признак Коши) . Для сходимости ряда (5.10) необходимо и достаточно, чтобы сходился несобственный интеграл

∞
∫ f (x)dx.	(5.11)

Замечание. Из расходимости ряда (5.10) следует расходимость несобственного интеграла (5.11) и наоборот.

Достоинство интегрального признака сходимости Коши состоит в исключительно высокой его чувствительности. Этот признак четко проводит различие между сходящимися и расходящимися рядами.

Пример 5.8. Исследовать на сходимость ряд Дирихле

	∞	1			p >0.
	∑			,

	n=1 np					1			1
Решение.	В данном случае		an =				. Значит,	f (x) =		, причем
									x p
функция f (x)	при x ≥1 непрерывна,					n p
					положительна,			монотонно убывает, и

f (n) = an . Это позволяет воспользоваться интегральным признаком Коши. Вычислим

∞

при p <1

x1−p

∞

−1

∫

при p >1.

x p

1− p

− p

∞

dx = ln | x |

= ∞ ( p =1).

∫

Таким образом, ряд Дирихле сходится

при p >1 и расходится при p≤1.

Частными случаями ряда Дирихле являются гармонический ряд

∞

∑

+... +

+...

n=1 n

и ряд обратных квадратов

∞

∑

+... +

+....

n=1 n

Как мы только что показали, первый из этих рядов расходится, а второй –

О.Л.Коши (1789-1857) – французский математик,П.Г.Дирихле (1805-1859) – немецкий математик.

сходится.

Пример 5.9. Исследовать сходимость ряда

∞			1
∑			1		.
∑	(1 + n2 )arctg				.
n =1	(1 + n2 )arctg			n
Решение. В данном случае	an	=	1				, поэтому рассмотрим
Решение. В данном случае	an	=	+ n2 )arctg				, поэтому рассмотрим
		(1	+ n2 )arctg			n

функцию	f (x) =	1	. Функция	f (x) непрерывна, положительна
		+ x2 )arctgx
	(1

и монотонно убывает на промежутке [1, +∞). Это позволяет воспользоваться интегральным признаком Коши. Вычислим несобственный интеграл

∞

∞ darctgx

= ln arctgx

∞

= ln

−ln

= ln 2.

∫

+ x2 )arctgx

1 (1

1 arctgx

Так как несобственный интеграл сходится, то сходится и данный ряд.

Сформулируем еще один признак сходимости положительных рядов.

Теорема 5.5. (Признак Даламбера) Если отношение последующего

члена

ряда

к предыдущему

an+1

начиная

с некоторого значения n,

удовлетворяет неравенству

an+1

≤ q <1,

где q

не зависит от n, то ряд

a1 + a2 +... + an +...,

(5.12)

сходится.

Если же наоборот, начиная с некоторого n, имеем

			an+1	≥1,
				≥1,
то данный ряд расходится.			an
то данный ряд расходится.
Следствие. Если lim	an+1	= l, то ряд (5.12) сходится при условии, что
Следствие. Если lim		= l, то ряд (5.12) сходится при условии, что
n→∞ a
	n
l < 1 и расходится, если l > 1 .						2n n!
					∞	2n n!
Пример 5.10. Исследовать сходимость ряда					∑		.
Пример 5.10. Исследовать сходимость ряда					∑	nn	.
					n =1	nn

Решение. Вычисляем отношение последующего члена к предыдущему.

Ж.Л.Даламбер (1717-1783) – французский математик, механик и философ-просветитель. 80

2n+1(n +1)!

2nn

(n +1)n+1 2n n! (n +1)n

Найдем предел

lim

2nn

= 2 lim

<1.

n→∞ (n +1)n

n→∞

Этот предел меньше единицы, поэтому данный ряд, в соответствии с признаком Даламбера, сходится.

∞ n2

Пример 5.11. Исследовать сходимость ряда ∑ .

n=1 5n

Решение. В соответствии с признаком Даламбера, найдем предел отношения последующего члена ряда к предыдущему

n2 5n−1

l = lim

= lim

lim

<1.

1 2

n→∞ an−1

n→∞ 5n (n −1)2

5 n→∞

−

Так как l <1, то данный ряд сходится.

∞

32n+1

Пример 5.12. Выяснить сходимость ряда

∑

32n +1

32n +3

n=1 23n−1

Решение. Здесь

an =

an +1 =

23n −1

23n +2

32n+3 23n−1

lim

n+1

= lim

>1.

n→∞

n→∞ 23n+2 32n+1

Этот предел больше единицы, поэтому данный ряд, в соответствии с признаком Даламбера, расходится.

Знакопеременные ряды. Знакочередующиеся ряды

Определение 5.3. Знакопеременным рядом называется ряд, членами которого являются вещественные или комплексные числа произвольного знака. Пусть

a1 + a2 +... + an +...,

(5.13)

некоторый знакопеременный ряд. Некоторую информацию относительно этого ряда можно получить, рассматривая ряд

a1		+		a2		+ +		an		+ ,	(5.14)

составленный из абсолютных величин членов ряда (5.13). Ряд (5.14) является, очевидно, положительным рядом и поэтому его можно изучать на основании приемов, уже рассмотренных нами.

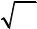
Теорема 5.6. Ряд (5.13) сходится, если сходится ряд (5.14). Определение 5.4. Знакопеременный ряд называется абсолютно

сходящимся, если сходится ряд, составленный из абсолютных величин его членов.

Абсолютно сходящиеся ряды во многих отношениях напоминают ряды с положительными членами. Для них можно ввести операцию умножения

рядов.

Пусть даны два ряда

∞

a1 +a2 +a3 +... +an +... = ∑an (5.15)

n=1

∞

b1 +b2 +b3 +... +bn +... = ∑bn. (5.16)

n=1

Рассмотрим ряд

∞

c1 +c2 +c3 +... +cn +... = ∑cn , (5.17)

n=1

	c1 = a1b1,
	c2 = a1b2 + a2b1,
	c2 = a1b2 + a2b1,
где	c3 = a1b3 + a2b2 + a3b1,
где	.....................................
	.....................................
	c	= a b	+ a b	+ a b	−2	+... + a b ,
	n	1 n	2 n−1	3 n	−2	n 1
	..............................................................

Ряд (5.17) будем называть произведением рядов (5.15) и (5.16). Приведем без доказательства следующую теорему.

Теорема 5.7. Если ряды (5.15) и (5.16) абсолютно сходятся, то ряд (5.17) тоже абсолютно сходится и его сумма равна произведению сумм исходных

рядов, так что если A,B и C - суммы рядов (5.15), (5.16) и (5.17), то

C = A B.

Замечание. При умножении неабсолютно сходящихся рядов может получиться расходящийся ряд.

Определение 5.5. Знакопеременный ряд называется условно сходящимся, если он сам сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Пример 5.13. Исследовать сходимость ряда

∞	1	1
∑(−1)2 n(n+1)		1	.
∑(−1)2 n(n+1)			.
n=1		n3

Решение. Выпишем несколько членов данного ряда

	1		1		1		1		1	1		n(n+1)	1
−1−		+		+		−		−		+... +(−1)	2			+...
	23				43		53		63				n3
		33												1
который, очевидно,	является				рядом		знакопеременным. Ряд						∞
													∑		,

													n =1	n3

составленный из абсолютных величин членов исходного ряда, сходится (как ряд Дирихле, где p = 32 >1), поэтому заданный ряд сходится абсолютно.

Определение 5.6. Знакопеременный ряд называется знакочередующимся, если соседние его члены имеют различные знаки, т.е. an an +1 < 0.

Например, знакочередующимся является ряд

1− 12 + 13 − 14 +... + (−1)nn+1 +...

Для знакочередующихся рядов имеется достаточно общий и практичный признак сходимости, доказанный Г.В. Лейбницем.

Теорема 5.8. (Признак сходимости Лейбница) . Если абсолютные величины членов знакочередующегося ряда

a	− a	2	+ a	3	−... + (−1)n +1 a	n	+ ...	(5.18)
1		2		3		n

образуют монотонно невозрастающую последовательность, стремящуюся к нулю, т.е. если

a1 ≥ a2 ≥ a3 ≥... ≥ an ≥...

lim an = 0 ,

n→∞

то ряд (5.18) сходится.

Ряд (5.18), удовлетворяющий условиям доказанной теоремы, будем называть рядом типа Лейбница.

Замечание. Оценим ошибку, которую мы совершаем, заменяя сумму ряда типа Лейбница его частичной суммой S n , т.е. оценим величину суммы

остатка rn :

rn = (−1)n cn +1 + (−1)n +1 cn + 2 + ...

Переписав rn в виде

rn = (−1)n (cn +1 − cn +2 + ...)

и замечая, что ряд, стоящий в скобках, есть снова ряд типа Лейбница, так что его сумма больше нуля и меньше cn+1, получаем для rn следующую оценку:

rn < cn +1.

Таким образом, ошибка имеет знак первого отброшенного члена и меньше его

Г.В.Лейбниц (1646-1716) – немецкий математик.

по абсолютной величине.
Пример 5.14. Исследовать сходимость ряда
	∞		(−1)n+1 n									1				2					3							(−1)n+1 n
	∑									=				−						+					−... +						+... .
	∑			n	2	+1				=		2		−	2	2				+	2				−... +			n	2	+1	+... .
	n=1			n		+1						2			2		+1 3					+1						n		+1
Решение. Применим признак Лейбница. Так как
	2			=		1					,					3			=		1			,			4			=	1		,... ,
22 +				=		1					,								=			1		,		4	2 +1			=		1	,... ,
22 +		1				1								32 +1								1				4	2 +1					1
						2 +														3	+									4	+
то						2 +		2												3	+	3								4	+	4
то							1						2					3								4
							1		>				2				>	3				>				4	>... .
						2			>			2	2				>	2			1	>	4			2	>... .
						2						2		+1				3		+	1		4			+1

Следовательно, первое условие признака Лейбница выполнено. Далее, так как

an =

то

lim a

= lim

= 0,

n2 +1

n →∞

n →∞ n2 +1

n →∞

n +

т.е. выполнено и второе условие. Значит, по признаку Лейбница, исходный ряд сходится.

Выясним теперь, сходится ли этот ряд абсолютно, т.е. сходится ли ряд

∞ n

∑ .

n=1 n2 +1

Воспользуемся вторым признаком сравнения положительных рядов. Сравним

∞

∞ 1

ряд

∑

гармоническим

рядом

∑

который, как

было показано,

n=1 n2 +1

n=1 n

расходится. Так как

= lim

> 0,

lim

n →∞ n

n →∞

∞

то

ряд

∑

также

расходится

и,

следовательно,

исходный ряд

n=1 n2 +1

∑∞ (−1)n +1 n

n =1 n2 +1 сходится условно.

Решение задач

Задача 5.1. Показать, что предлагаемый ниже ряд расходится.

∞	5n−1 +1		2		6		26		5n−1 +1
∑		=		+		+		+... +		+... .
∑	n	=	5	+	25	+	125	+... +	n	+... .
n=1	5		5		25		125		5
					84

Решение. Действительно, предел общего члена этого ряда не равен нулю:

lim an = lim

5n−1 +1

= lim

≠ 0,

n→∞

т.е. необходимый признак сходимости ряда не выполняется, следовательно, ряд расходится.

Задача 5.2. Исследовать сходимость ряда

∞

∑

= 3

+... +

+....

n=1

Решение. Сравним его с рядом:

∞

∑

=1+

+... +

+...,

n=1 n

который расходится, так как является гармоническим рядом. Для общих членов этих двух рядов имеем следующее соотношение

1 < 3n n n .

Так как гармонический ряд расходится, то по первому признаку сравнения расходится и рассматриваемый ряд.

∞	1
Задача 5.3. Исследовать сходимость ряда ∑			.
	n	−2
n=1	4 3

Решение. Воспользуемся вторым признаком сравнения рядов. Для этого наряду

∞

с исходным рядом рассмотрим ряд

∑

общий член

которого b =

n=1 3n

является членом геометрической прогрессии со знаменателем

q =

Вычислим предел отношения общих членов этих рядов

lim

= lim

4 3n −2

n→∞ bn

n→∞

n→∞ 4 −

Так как

предел

отношения общих

членов

рассмотренных

рядов

конечен,

∞

отличен

от нуля,

а ряд

сравнения

∑

сходится,

то,

соответствии со

n=1

вторым признаком сравнения, сходится и данный ряд.

Задача 5.4. Исследовать сходимость ряда

∞

∑

+...+

+....

n=1 n

Решение. В данном случае a

, поэтому рассмотрим функцию f (x) =

. Функция f (x) непрерывна,

положительна

монотонно убывает на

промежутке [1, +∞). Это позволяет воспользоваться интегральным признаком Коши. Вычислим несобственный интеграл:

∞	1	∞	1		1	∞

∫		dx = ∫d (−		) = −			=1.
	x2		x		x	1
1		1

Так как несобственный интеграл сходится, то сходится и данный ряд.

∞ n3

Задача 5.5. Исследовать сходимость ряда ∑ n .

n=1 e

Решение. Вычислим отношение последующего члена к предыдущему:

a	n +1	=	(n +1)	3 en		=	(n +1)	3	.
an			en+1		n3		n3e

В соответствии с признаком Даламбера, найдем предел этого отношения:

(n +1)3

1 3

lim

lim 1

<1.

n3e

n→∞

e n→∞

Этот предел меньше единицы, поэтому делаем вывод, что данный ряд сходится.

∞	n!
Задача 5.6. Выяснить сходимость ряда ∑		.
	n
n=1	2 +1

Решение. Используем признак Даламбера. Здесь

lim an+1

n→∞ an

	a	=		n!		,

	n		2n +1

= lim	(n +1)!				(2n +1)
		+1)			n!
n→∞ (2n+1

(n +1)!

n+1

2n+1 +1

(n +1)

(1+

)

= lim

n→∞ 2n+1 (1 +

)

2n+1

(n +1) 2n

(1+

)

= lim

lim

lim(n +1)

=∞ >1.

2n+1

n→∞

(1+

)

2 n→∞

2n+1

Найденный предел превосходит единицу, следовательно, рассмотренный ряд расходится.

Задача 5.7. Исследовать сходимость ряда

∞

(−1)n+1

∑

=1−

−... +

+... .

n=1

Решение. Применим признак Лейбница. Так как

1 >

>... >

>..., то

первое условие признака Лейбница выполнено. Далее,

так как

, то

lim a

= lim

= 0,

т.е.

выполнено и второе условие.

Значит,

по признаку

n→∞ n

n→∞ n2

сходится. Выясним теперь, сходится

Лейбница исходный

ряд

ли этот

ряд

∞

абсолютно, т.е. сходится ли ряд ∑

. Используя интегральный признак Коши,

n=1 n

∞

можно убедиться (см. пример 5.4), что ряд

∑

сходится и, следовательно,

(−1)n+1

n=1 n

∞

исходный ряд ∑

сходится абсолютно.

n=1

Вопросы для самопроверки по теме 5.1

1. Как

называется сумма Sn = a1 + a2 +... + an

первых

членов

ряда

a1 + a2 +... + an +...?

2. Как называют конечный предел lim Sn =S ?

n→∞

3.Какой ряд называется сходящимся?

4.Какой ряд называется расходящимся?

5. Чему равна сумма ряда αa1 +αa2 +... +αan +..., если сумма ряда a1 + a2 +... + an +...равна S ?

∞

6. Чему равна сумма ряда∑(αn +βn ), если соответствующие суммы двух

n=1

∞	∞
рядов равны соответственно ∑αn = A и	∑βn = B?
n=1	n=1

7.Изменится ли свойство сходимости или расходимости ряда, если у ряда отбросить или приписать к нему любое конечное число членов с начала ряда?

8.Сформулируйте необходимый признак сходимости ряда.

9.Следует ли сходимость ряда из стремления общего члена ряда к нулю?

10.Как называют ряд 1+12 +13 +...+ 1n +...? Сходится ли этот ряд?

11.Сформулируйте первый признак сравнения положительных рядов.

12.Сформулируйте второй признак сравнения положительных рядов.

13.Сформулируйте интегральный признак сходимости Коши.

14.Сформулируйте признак Даламбера сходимости рядов.

15.Какой ряд называется знакопеременным рядом?

16.Какой ряд называется абсолютно сходящимся рядом?

17.Дайте определение операции умножения рядов.

18.Чему равна сумма ряда, полученного в результате умножения двух абсолютно сходящихся рядов?

19.Какой ряд называется условно сходящимся?

20.Какой ряд называется знакочередующимся?

21.Какой ряд будем называть рядом типа Лейбница?

22.Сформулируйте признак сходимости Лейбница?

23.Оцените ошибку, совершаемую при замене суммы ряда типа Лейбница его частичной суммой.

5.2. Функциональные ряды

При изучении функциональных рядов Вам предстоит ознакомиться со следующими вопросами:

•Функциональные ряды и их свойства.

•Степенные ряды и их свойства.

•Разложение функций в степенные ряды. Ряд Тейлора.

•Применение степенных рядов к приближенным вычислениям.

После изучения теоретического материала следует ответить на вопросы для самопроверки и на вопросы теста №9. При возникающих затруднениях в ответах обратитесь к [2].

Студентам очно-заочной и заочной форм обучения надо решить одну задачу из контрольной работы № 6 под номерами 41-50 в соответствии со своим

вариантом.

Функциональные ряды и их свойства

Пусть u1 (x), u2 (x),..., un (x),... - функции, определенные на некотором

множестве X вещественных чисел, которые могут принимать		как
вещественные, так и комплексные значения. Можно считать также,	что	x -
точки, принадлежащие множеству E точек комплексной плоскости,	и тогда
u1 (x), u2 (x),..., un (x),... -функции комплексной переменной x .
Определение 5.8. Символ
u1 (x) +u2 (x) +... +un (x) +...	(5.19)
называется функциональным рядом на множестве X .

Если переменная x принимает только вещественные значения, и функции u1 (x), u2 (x),..., un (x),... - также все вещественные, то ряд (5.19)

называется вещественным. В противном случае ряд называется комплексным. В дальнейшем в основном рассматриваются только вещественные ряды.

Придав в выражении (5.19) переменной x некоторое значение	x0 из
множества X , мы получим числовой ряд
u1 (x0 ) +u2 (x0 ) +... +un (x0 ) +... .	(5.20)

В зависимости от значения, принимаемого переменной x, числовой ряд (5.20) может оказаться сходящимся или расходящимся.

Определение 5.9. Множество всех значений переменной x , для которых сходятся ряды (5.20), называется областью сходимости функционального ряда

(5.19).

Пример 5.15. Ряд		x	+	x2	+	x3	+... +	xn	+...
	2			22		23		2n

при каждом фиксированном	x = x0			представляет				собой геометрическую

прогрессию со знаменателем x20 . Условие сходимости этого ряда состоит в том,

что x20 <1. Таким образом, область сходимости рассматриваемого ряда

состоит из всех тех значений переменной x, для которых \| x\|<2.
Пример 5.16. Члены функционального ряда
	1	+		1		+... +			1		+...	(5.21)
	2		2	+ x	2		n	2	+ x	2
1+ x			2

при любом x меньше соответствующих членов ряда обратных квадратов


1+	1	+	1	+... +		1		+...,
	2		2			2
	2		3			n
			1			1
т.е.					≤				.
			n2 + x2				n2

Так как последний ряд сходится, то по первому признаку сравнения при любом x должен сходиться и ряд (5.21). Таким образом, областью сходимости ряда (5.21) является вся числовая ось −∞ < x < +∞.

Если ряд (5.19) сходится в промежутке (a,b) и имеет сумму S(x), то это означает, что при любом фиксированном x из (a,b), задав произвольное положительное число , можно найти такое N , что при всех значениях n > N остаток ряда rn (x) = S(x) − Sn (x) удовлетворяет неравенству | rn (x) |< ε.

Необходимо особо отметить, что N , вообще говоря, зависит от выбранного значения x , т.е. N = N(x).

Определение 5.10. Если при любом заданном ε > 0 можно найти такое число N , не зависящее от x , чтобы при любом значении x из промежутка

(a,b) выполнялось неравенство | rn (x) |< ε при всех n>N, то ряд (5.19)

называется равномерно сходящимся в промежутке (a,b).

Равномерно сходящиеся ряды обладают целым рядом замечательных свойств, которые мы сформулируем, опустив доказательства.

1. Если члены ряда (5.19) - непрерывные в интервале(a,b) функции и ряд сходится равномерно, то его сумма S(x) - также непрерывная в интервале(a,b) функция.

2. Если члены ряда (5.19) - непрерывные в интервале (a,b) функции, ряд сходится равномерно и S(x) - его сумма, то функциональный ряд интегралов

y	y	y
∫u1 (x)dx + ∫u2 (x)dx +... + ∫un (x)dx +...,
α	α	α

где a < α < y <b, также сходится равномерно в промежутке (a,b) и имеет суммой функцию

∫ S(x)dx.

3. Пусть ряд (5.19) сходится в интервале (a,b) к сумме S(x) , а его

члены имеют на этом промежутке непрерывные производные, причем составленный из производных ряд

u ′(x) +u ′(x) +... +u ′(x) +...			(5.22)
1	2	n

сходится на (a,b) равномерно и имеет сумму σ(x). Тогда ряд (5.19) сходится на (a,b) равномерно и производная его суммы S(x) равна сумме ряда (5.22)

dS(x)	=σ(x).	(5.23)
dx

Очень удобный признак равномерной сходимости функционального ряда был предложен К.Т. Вейерштрассом. Пусть дан ряд.

u1 (x) +u2 (x) +... +un (x) +...,

(5.24)

члены которого определены в интервале (a,b).

Теорема 5.10. (Признак Вейерштрасса) . Функциональный ряд (5.24)

сходится абсолютно и равномерно в интервале (a,b), если существует сходящийся числовой ряд с положительными членами

∞

c1 +c2 +... +cn +... = ∑cn , (5.25)

n=1

члены которого превосходят абсолютные величины соответствующих членов

ряда (5.24) при всех x из интервала (a,b), т.е.

| un (x) |≤ cn

(n =1, 2,...).

Пример 5.17. Функциональный ряд

sin x

sin(22 x)

+... +

sin(n2 x)

+...

потому что при всех x и при

сходится равномерно для всех вещественных x ,

всех n

sin(n2 x)

≤

а ряд обратных квадратов

1+ 212 + 312 +... + n12 +...,

как было показано, сходится.

Степенные ряды и их свойства

Одним из важнейших примеров функциональных рядов являются ряды

вида

a	+a z +a z2		+...+a zn +...,	(5.26)
0	1	2	n

которые называются степенными рядами.

Числа a1, a2 , a3 ,..., an ,... называются коэффициентами этого ряда. Как и

в случае общих функциональных рядов, можно говорить о вещественных и о комплексных степенных рядах. А именно, если переменная z принимает комплексные значения, а коэффициенты ряда - комплексные числа, то

К.Т.Вейерштрасс (1815-1897) – немецкий математик.

степенной ряд называют комплексным. Если же значения z могут быть только вещественными, а коэффициенты ряда - также вещественные числа, то

степенной ряд называют вещественным.				z	- вещественные,
Промежуточный	случай,	когда	значения	z	- вещественные,	а
коэффициенты ряда	могут	быть	комплексными		(an = bn +icn ) ,	не

представляет большого интереса, так как в этом случае всю нужную информацию о ряде

(b0 +ic0) +(b1 +ic1)z +...+(bn +icn)zn +...

можно получить, рассматривая два вещественных ряда

b0 +b1z +...+bnzn +...

c0 +c1z +...+cnzn +...

Области сходимости степенных рядов устроены довольно просто. Они описываются теоремой Абеля.

Теорема 5.11. (Абеля) . Если степенной ряд (5.26) сходится при некотором значении z = z0 , то он сходится абсолютно при всех значениях z ,

для которых | z |<| z0 | . Наоборот, если он расходится при z = z0 , то расходится и при всех значениях z , для которых | z |>| z0 | .

Из теоремы Абеля вытекает следующее очевидное следствие. Следствие. Существует неотрицательное число R , которое называется

радиусом сходимости ряда (5.26), и которое обладает следующими

свойствами:

1)ряд (5.26) сходится абсолютно при | z |< R,

2)ряд (5.26) расходится при | z |> R.

Множество всех комплексных чисел, для которых | z |< R, образует на

плоскости комплексных чисел круг радиуса R с центром в точке 0. Этот круг называется кругом сходимости ряда (5.26).

Если ряд	a	0	+ a x + a	2	x 2	+ ... + a	n	x n + ...	(5.27)
		0	1	2			n
имеет вещественные	коэффициенты				и	переменная x			принимает только

вещественные значения, то из теоремы Абеля следует утверждение:

Существует такое неотрицательное число R , что при x > R или x < −R ряд (5.27) расходится, при −R < x < R - сходится абсолютно, а поведение ряда при x = ±R подлежит дальнейшему анализу.

Множество значений переменной x , удовлетворяющих соотношению −R < x < R , называется в случае вещественного ряда его интервалом сходимости. За числом R , как и в комплексном случае, сохраняется название

радиуса сходимости.

Рассмотрим вещественные степенные ряды более подробно.

Теорема 5.12. Степенной ряд равномерно сходится в любом замкнутом

Н.Х.Абель (1802-1829) – норвежский математик.

интервале, содержащемся в его интервале сходимости.

Из теоремы о равномерной сходимости степенного ряда, а также из теорем о возможности почленного дифференцирования и интегрирования равномерно сходящихся рядов следует, что степенные ряды можно почленно дифференцировать и интегрировать. Более того, можно показать, что

почленное дифференцирование и интегрирование не меняет радиуса сходимости исходного ряда.

Покажем, как можно определить радиус сходимости степенного ряда. Пусть имеется ряд (5.27). Рассмотрим ряд, составленный из абсолютных величин его членов

\| a	0	\| + \| a x \| + \| a	2	x2	\| +...+ \| a	n	xn \| +...	(5.28)
	0	1	2			n

Для определения сходимости последнего положительного ряда применим признак Даламбера. Допустим, что существует предел

xn+1

| a

lim

n+1

=| x | lim

=| x | L.

a xn

| a

n→∞

Тогда по признаку Даламбера ряд сходится,

если

| x | L <1, т.е. если | x |<

, и

расходится, если L | x |>1, т.е. если | x |> L1 .

Следовательно, ряд (5.28) сходится абсолютно при | x |< L1 . Если же

| x |> L1 , то ряд (5.28) расходится и, как было показано в процессе

доказательства признака Даламбера, общий член этого ряда не стремится к нулю. Но тогда общий член исходного степенного ряда (5.27) также не стремится к нулю, и так как не выполнен необходимый признак сходимости, то этот ряд расходится.

Таким образом, интервалом сходимости степенного ряда (5.27) будет

интервал − 1 , 1 , где радиус сходимости равен

L L

R =

= lim

n→∞

n+1

Пример 5.18. Исследовать сходимость степенного ряда

∞

x3 +... +

∑

= x +

+....

n =1

Решение. В данном

случае

Найдем радиус

n +1

−1+ 12 −13 +... +(−1)n+1 1n +...,

сходимости ряда

R = lim		an	= lim	n +1	= lim 1	+	1	=1.
R = lim	a		= lim	n	= lim 1	+		=1.
n→∞	a		n→∞	n	n→∞		n
		n+1

Следовательно, рассматриваемый ряд абсолютно сходится для значений x , удовлетворяющих неравенству −1 < x <1.

Исследуем сходимость ряда на концах промежутка. Если x =1, то мы получаем гармонический ряд

1+ 12 +13 +...+ 1n +...,

который, как было показано, расходится.

Если же x =−1, то получается знакочередующийся ряд

удовлетворяющий всем условиям признака Лейбница, и, значит, этот ряд сходится. Итак, исходный ряд абсолютно сходится при −1 < x < 1 и условно сходится при x = −1.

Пример 5.19. Найти область сходимости степенного ряда

∞

∑nn (x +3)n.

n=1

Решение. Полагая x+3=t, получим ряд

∞

∑nntn.

n=1

Здесь an = n n ,

an +1 = (n +1)n +1. Вычислим R :

R=lim

=lim

lim

=0.

an+1

1 n

n→∞

n→∞(n+1)n+1

n→∞(n+1)n(n+1)

n→∞

en→∞n+1

(n+1)

∞

Ряд ∑nnt n сходится только при t = 0, поэтому исходный ряд сходится

n=1

только для x = −3 и расходится для всех остальных значений x .

Разложение функций в степенные ряды. Ряд Тейлора

Сумма всякого сходящегося вещественного степенного ряда является некоторой функцией, определенной внутри интервала сходимости этого ряда. В связи с этим возникают две задачи. Во-первых, можно по заданному ряду искать ту функцию, которой равна его сумма в интервале сходимости ряда. Эта

Б.Тейлор (1685-1731) - английский математик.

задача называется суммированием сходящегося ряда. Во-вторых, можно по заданной функции искать сходящийся ряд того или иного типа, сумма которого в интервале сходимости равнялась бы заданной функции. Эта задача называется разложением функции в ряд. Сейчас мы займемся вопросами разложения функций в степенные ряды. Заметим, что наряду со степенными рядами вида

a0 +a1x +a2x2 +...+anxn +...

нам будет удобно рассматривать также ряды вида

a0 +a1(x −x0) +a2(x −x0)2 +...+an(x −x0)n +... .

Ясно, что подстановкой y = x − x0 второй ряд превращается в первый.

Поэтому,	если интервалом	сходимости	первого ряда будет \| x \|<R, то
интервалом сходимости второго \| x − x0 \|< R.
Если	функция f (x)	на некотором	промежутке (a −h, a +h) имеет

производные всех порядков, то для любого

x из этого промежутка можно

записать формулу Тейлора любого порядка n :

f (x) = f (a) +

f '(a)

(x − a) +

f ''(a)

(x − a)2 + ... +

f (n) (a)

(x − a)n + Rn (x),

где остаточный член Rn ( x)

может быть представлен в виде

R (x) =

f (n+1) (c)

−a)n+1,

(n +1)!

здесь c -точка, расположенная между a и x .

Положим при любом n=1,2,..

f (n) (a)

(a) +

f '(a)

(x −a) +

f ''(a)

(x −a)2 +... +

(x −a)n = Sn (x).

Тогда

f (x) − Sn (x) = Rn (x).

Если

lim Rn ( x) = 0,

то ряд

n→∞

f (n) (a)

f (a) +

f ' (a)

(x − a) +

f '' (a)

(x − a)2 +... +

(x − a)n +...

сходится и его суммой будет функция f (x).

Определение 5.11. Представление функции f (x) в виде ряда

f (x) = f (a) +	f '(a)	(x −a) +	f ''(a)	(x −a)2	+...+	f (n) (a)
						n!
1!		2!

называется разложением этой функции в ряд Тейлора.

(x −a)n +... (5.29)

В частности, при a = 0 разложение в ряд Тейлора называется

разложением в ряд Маклорена .

f (x) = f (0) +	f '(0)	x +	f ''(0)	x	2	+... +	f (n) (0)	x	n	+...	(5.30)
	1!		2!				n!

Удобный для практических приложений признак разложимости функции f (x) в ряд Тейлора дает следующая теорема.

Теорема 5.13. Если функция f (x) имеет на промежутке (a −h, a +h) производные всех порядков, и для всех x из этого промежутка существует такая постоянная L , что при любых n и x (a −h, a +h) выполняется неравенство | f ( n ) ( x) |≤ L, то функция f (x) разлагается в ряд Тейлора (5.29).

Можно показать, что если разложение функции в какой-либо степенной ряд вообще возможно, то оно является разложением именно в ряд Тейлора. Другими словами, имеет место следующая теорема:

Теорема 5.14. Пусть ряд

c0 +c1(x −a) +c2(x −a)2 +...+cn(x −a)n +...

сходится в некотором интервале (a −R,a +R) к функции f (x). Тогда этот ряд является рядом Тейлора функции f (x) , т.е.

	f (x) =c			+c (x −a) +c (x −a)2 +...+c (x −a)n +...,
		0		1		2	n
где	c	=	f (n) (a)		.
где	c	=			.
	n		n!
			n!
В качестве примера найдем разложение в ряд Маклорена функции
f ( x) = ex .
Поскольку			(e x ) ' = e x ,			(e x ) '' = e x , ..., (e x )( n )	= e x , ..., то
				f (0) = f ' (0) = ... = f ( n ) (0) = ... = 1.

Подставим найденные значения производных в формулу (5.30) и получим искомое разложение:

∞ xn

ex =1 +

+... +

+...,

или

=n∑=1 n!

(5.31)

В частности, при x = 1 получаем выражение для e, весьма удобное для вычисления e с любой степенью точности

e =2 + 21!+...+ n1!+... .

Пример 5.20. Воспользовавшись формулой (5.31), разложить в ряд Маклорена функцию f ( x) = 32 x +1.

Решение. Заметим, что 32 x+1 = 3 32 x = 3e2 x ln 3. Тогда, заменяя в

К.Маклорен (1698-1746) - шотландский математик.

равенстве (5.121) x на 2 x ln 3 , получим			n
e2xln3 =	∞	(2 ln 3)
	∑		xn ,
	n=1	n!

и, умножая обе части последнего соотношения на 3, придем к искомому разложению

32x+1 =3 ∑∞ (2ln3)n xn.

n=1 n!

Так как разложение для ex имеет место на всей числовой оси, то и построенное

разложение функции 32 x+1 справедливо для любого x . Пример 5.21. Написать разложение в ряд Тейлора функции

f (x) = 6

− x2 −2x +8

в окрестности точки a =1.

Решение. Разложим данную дробно-рациональную функцию на

простейшие дроби:

−6

− x2 −2x +

+ 4)(x −2)

x +

x −2

Коэффициенты

находятся

из

тождества

−6 = A(x −2) +B(x +4),

которое верно для любого значения

x . Полагая

x = 2 , получим B = −1, а полагая x = −4 , имеем A =1. Следовательно,

(5.32)

x +4

− x

− x2 −2x +8

Представим каждое из слагаемых, стоящих в правой части этого равенства, в виде геометрического ряда, расположенного по степеням x −1. Имеем

1	=		1		.
2 − x		1−(x		−1)

Дробь, стоящую справа, можно рассматривать как сумму геометрической

прогрессии с первым членом 1 и знаменателем q = x −1:
	1	=1+(x −1)	+(x −1)2 +... +(x −1)n +...
1−(x −1)		=1+(x −1)	+(x −1)2 +... +(x −1)n +...
1−(x −1)
или		1	∞
		1	∞
			= ∑(x −1)n .	(5.33)
		1 − (x −1)	= ∑(x −1)n .	(5.33)
		1 − (x −1)	n=0
Это разложение имеет место для			\| x −1\|<1, т.е. для	−1 < x −1 < 1 или

0 < x < 2 . Первую дробь, стоящую в правой части равенства (5.32), запишем в виде

4 + x

5 + ( x −1)

1 +

x −1

Выражение

представляет

собой

сумму

геометрической

1 +

x −1

прогрессии,

первый

член

которой

a = 1

знаменатель

q =−

Следовательно

x −1

4 + x

−

−5

+...+

+...

−5

(−1)n (x −1)n

∞

или

∑

(5.34)

4 + x

5 n=0

Ряд,

стоящий

справа,

сходится для

x −1

<1,

т.е.

| x −1|<5 или

− 5

− 4 < x < 6. Подставляя ряды (5.33) и (5.34) в равенство (5.32), получим

∞

(−1)n (x −1)n

= ∑ (x −1)n

∑

−x2 −2x +8

n=0

5 n=0

или окончательно

(−1)n

∞

= ∑

n+1

(x −1)n.

− x

− 2x +8

n=0

Построенное разложение имеет место в области пересечения областей сходимости рядов (5.33) и (5.34), т.е. для 0 < x < 2.

Применение степенных рядов к приближенным вычислениям

Рассмотрим применение вещественных степенных рядов к приближенным вычислениям.

Во-первых, ряд Тейлора, и в частности ряд Маклорена в случае его сходимости, дает возможность приближенно вычислять значения функции f (x) , заменяя их конечным числом членов разложения по формуле (5.29).

Чем меньше | x −a |, тем меньше членов можно брать в этом разложении для

| x −a |

вычисления f (x) с желаемой точностью. Если весьма мало, то иногда

достаточно ограничиться только первыми двумя членами, отбросив все остальные. Таким образом, получается очень простая приближенная формула

для f (x) , которая при малых | x −a | вполне может заменить часто довольно

сложное точное выражение для f (x) . Например, из разложения функции ex в

ряд Маклорена следует, что

ex ≈1 + x.

Аналогично могут быть получены формулы:

sin x ≈ x,	cos x ≈1−	x2	,	tg x ≈ x,
		2
					x
ln(1+ x) ≈ x,	(1+ x)n ≈1+nx,			n 1+ x ≈1+		.

					n

Пользуясь этими приближенными формулами при x , близких к нулю (положительных или отрицательных), можно значительно упростить сложные выражения.

Во-вторых, с помощью рядов можно вычислять определенные интегралы.

Большое значение, например, в теории вероятностей имеет интеграл

1	x	x2
	∫e−		dx,
		2

2π 0

который не может быть выражен в элементарных функциях. Для его

вычисления заменим в формуле (5.31)

x на −

. Тогда

x2 n

−

x2 2

e 2

=1−

−

+... +

−

+....

Радиус сходимости R полученного ряда равен ∞, т.е. на любом замкнутом промежутке [0, x] этот ряд сходится равномерно. Это позволяет почленно проинтегрировать его, что дает следующее равенство:

e−

dx =

1−

−

+... +(−1)n

x2n

+...

dx =

2π ∫0

2 22

2! 23 3!

2n n!

2π ∫0

x2n+1

x −

−... +(−1)

+... .

2π

2 3

5 2

(2n +1)2

В-третьих, при помощи степенных рядов можно также приближенно

интегрировать разнообразные дифференциальные уравнения. Не вдаваясь в сложные теоретические соображения, ограничимся рассмотрением примеров.

Пример 5.22. Решить задачу Коши для уравнения первого порядка y ' = x 2 + y 2 , y (0) = 1.

Решение. Полагая x=0, из уравнения и начального условия находим y' (0) = 0 + ( y(0)) 2 = 1.

Если продифференцировать обе части уравнения, а затем положить x = 0 и использовать полученное равенства и начальные условия, то получим

y''=2x +2yy',

y''(0) =2 0 +2 1 1 =2.

Аналогично приходим к равенствам

y' ' ' = 2 + 2( y ' ) 2 + 2 yy ' ' ,

y ' ' ' (0) = 2 + 2 1 + 2 1 2 = 8,

y ( 4 ) = 6 y ' y ' '+2 yy ' ' ' ,

y ( 4 ) (0) = 6 1 2 + 2 1 8 = 28

и т. д. Подставляя полученные значения в формулу Маклорена, имеем

y'(0)

y''(0)

y(x) = y(0) +

x +

+... =1+ x + x

+ 3 x

6 x

+....

Этой формулой можно пользоваться при небольших значениях | x |.

Для решения дифференциальных уравнений широко используются также степенные ряды с неопределенными коэффициентами. Рассмотрим пример.

Пример 5.23. Решить уравнение второго порядка

y''+xy =0.

Решение. Будем искать решение в виде ряда по степеням x

y(x) =a0 +a1x +a2x2 +...+anxn +... .

После дифференцирования этого ряда и подстановки его в уравнение, получим следующее равенство

(1 2a2 +2 3a3x +3 4a4x2 +...)+x(a0 +a1x +a2x2 +...)=0.

Приравнивание нулю коэффициентов при x 0 , x1 , x 2 ,... дает систему уравнений

1 2a2 =0, 2 3a3 +a0 =0, 3 4a4 +a1 =0,

4 5a5 +a2 =0,

5 6a6 +a3 =0,

6 7a7 + a4 =0,...,

откуда последовательно находим коэффициенты ряда

a2 = 0, a3 = −

, a4

= −

, a5 = −

= 0,

2 3

3 4

4 5

a6 = −

a7 = −

= −

= 0

2 3 5 6

6 7

3 4 6

7 8

5 6

и т.д.

Подстановка этих результатов в степенной ряд дает общее решение рассматриваемого уравнения:

100

y ( x ) = a 0 + a1 x + a 2 x 2 + ... =

= a 0	+ a1 x −						a 0			x	3		−			a1		x	4	+		a 0			x	6		+				a1			x	7	− ... =
= a 0	+ a1 x −					2		3		x			−		3		4	x		+	2	3 5 6			x			+		3 4 6 7					x		− ... =
						2		3							3		4				2	3 5 6								3 4 6 7
					x		3							x		6												x	4				x	7
=	a	0	1	−	x				+					x					− ...			+ a	1	x	−			x			+		x				− ... .
=	a		1	−	2 3				+			2 3 5 6							− ...			+ a		x	−		3 4				+	3	4 6			7	− ... .
					2 3							2 3 5 6															3 4					3	4 6			7

Константы a0 и a1 остаются в качестве произвольных постоянных. Ряды же,

стоящие в скобках, представляют собой два линейно независимых частных решения исходного уравнения.

Решение задач

Задача 5.8. Исследовать область сходимости функционального ряда

sin x

sin(2x)

+... +

sin(nx)

+... .

sin(nx)

Решение.

Так

как

при

всех

≤

а ряд

1 +

+... +

+... ,

будучи

геометрическим,

со

знаменателем

геометрической

прогрессии

сходится,

то,

согласно

признаку

Вейерштрасса,

данный ряд сходится равномерно для всех вещественных x.

Задача 5.9. Исследовать область сходимости степенного ряда

∞ (x −1)n

(x −1)

(x −1)2

(x −1)3

(x −1)n

∑

+... +

+... .

n 3n

1 31

2 32

n=1

Решение. В данном случае Un (x) =

(x −1)n

Un+1(x) =

(x −1)n+1

(n +1) 3(n+1)

n 3n

Найдем радиус сходимости ряда, используя признак Даламбера. Для этого вычислим предел отношения последующего члена ряда к предыдущему:

Un+1

(x −1)n+1 n 3n

(x −1) n

lim

= lim

(n +1) 3n+1 (x −1)n

(n +1) 3

n→∞

x −1

lim

x −1

n→∞ n +1

Полученный предел, в соответствии с признаком Даламбера, для сходящегося ряда должен быть меньше единицы, т.е. x 3− 1 < 1 . Отсюда мы получаем

неравенство, определяющее	интервал	сходимости ряда	x −1	< 3 . Искомый

радиус сходимости будет	R = 3 .	Следовательно, рассматриваемый ряд
	101

абсолютно сходится для значений x , удовлетворяющих неравенству

−3 < x −1 < 3 или −2 < x < 4 .

Исследуем сходимость ряда на концах промежутка. Если x = −2 , то мы

получаем знакочередующийся числовой ряд
∞	(−1)n		1		1		(−1)n
∑		= −1 +		−		+... +		+...,
∑	n	= −1 +	2	−	3	+... +	n	+...,
n=1	n		2		3		n

который является рядом Лейбница и сходится. Причем сходится неабсолютно, так как ряд, составленный из абсолютных величин членов исходного ряда, расходится, будучи гармоническим рядом.

Если же x = 4 , то получается гармонический ряд

∞	1		1		1		1
∑		=1+		+		+... +		+...,
			2		3		n
n=1 n

который расходится. Итак, исходный ряд сходится абсолютно при −2 < x < 4 и сходится условно при x = −2 .

Замечание. При вычислении радиуса сходимости с помощью формулы

R = lim	an	, где a и a	n +1	- коэффициенты степенного ряда
R = lim	an+1	n	n +1
n→∞	an+1

a0 + a1 x + a2 x2 + ... + an xn + ... ,

будет получен тот же результат. Но следует быть внимательным в случае, когда в ряде пропущено бесконечно много членов, например, четной или нечетной степени. В этом случае лучше непосредственно применять признак Даламбера. Рассмотрим пример.

Задача 5.10. Найти область сходимости и радиус сходимости степенного

ряда	(x −5)2n−1
∞	(x −5)2n−1
∑		.
∑	2n 9n	.
n=1	2n 9n

Решение. Этот ряд содержит члены только с нечетной степенью, а бесконечное число членов с четной степенью отсутствует. Для нахождения области сходимости и радиуса сходимости применим непосредственно признак Даламбера.

Здесь общий член ряда и следующий за ним член соответственно равны

Un (x) =

(x −5)2n−1

, U n+1 ( x) =

( x − 5)2 n+1

2(n +1) 9n+1

2n 9n

Вычислим предел их отношения

lim

Un+1(x)

= lim

(x −5)2n+12n 9n

= (x −5)2

lim

(x −5)2 .

Un (x)

(x −5)2n−12(n +1) 9n+1

n→∞

n→∞ 2(n +1)

Полагая найденный предел меньше единицы,

т.е.

(x −5)2

<1,

приходим к

102

неравенству (x −5)2 < 9 или	x − 5	< 3 .

Искомый радиус сходимости	R = 3 , интервал сходимости −3 < x −5 < 3 или

2<x<8. Подстановка в заданный ряд x =2 или x = 8 приводит соответственно к рядам

∞

2n−1

∞

2n −1

∞

∑

−3

= −∑

3 3

= −

∑

2n 9n

n=1

6 n=1 n

которые получаются из расходящегося гармонического ряда почленным

умножением на − 16 и на 16 . Эти ряды также расходятся в соответствии со

свойством умножения ряда на число. Таким образом, областью сходимости

заданного ряда будет интервал 2<x<8.

Задача 5.11. Написать разложение в ряд Тейлора функции

f (x) =

в окрестности точки x =1,

+ x −6

т.е. написать разложение функции по степеням

(x −1) .

Решение. Разложим данную дробно-рациональную функцию на сумму

простейших дробей.

x2 + x −6

(x −2)(x +3)

x −2

x +3

Коэффициенты A и B находятся из тождества

5 x = A( x + 3) + B( x − 2) ,

которое верно для любого значения x .

Полагая

x = −3 , получим

B =3 , затем,

полагая x = 2 , будем иметь A=2. Следовательно,

5 x

x2 + 2 x − 3

x − 2

x + 3

Представим каждое из слагаемых, стоящих в правой части этого равенства, в виде геометрического ряда, расположенного по степеням (x −1) . Для этого первое слагаемое представим в виде

2		1
		= −2		.
	x − 2		1 −(x −1)
Дробь, стоящую справа, можно		рассматривать как сумму геометрической
		103

прогрессии с первым членом 1 и знаменателем q = x −1

1=1+(x −1) +(x −1)2 +... +(x −1)n +...

1−(x −1)

Витоге для первого слагаемого имеем:


2				1	∞
			= −2		= −2∑(x −1)n .
	x − 2			1 −(x −1)
					n=0
Это разложение имеет		место		для \| x −1\|<1, т.е. для −1 < x −1 < 1 или
0 < x < 2 .

Вторую простейшую дробь, стоящую в правой части равенства, запишем в виде

= 3

x + 3

4 + ( x −1)

x −1

1 +

Выражение

представляет

собой

сумму геометрической

1 +

x −1

прогрессии, первый

член

которой

a = 1 ,

знаменатель q = −

Следовательно, для второго слагаемого можно записать

x −1

x −1 2

x −1

+... +

+...

x +3

−4

или в сокращенной записи

3 ∞

(−1)n (x −1)n

∑

x +3

4 n=0

Этот ряд сходится при условии

x −1

<1, т.е. для

| x −1 |< 4

или −3 < x <5 .

−4

Подставляя

найденные

разложения

правую

часть

равенства

5 x

, получим

x2 + 2 x − 3

x − 2

x + 3

∞

3 ∞ (−1)n (x −1)n

= −2∑

(x −1)

∑

+ 2x −3

x −

n=0

4 n=0

Окончательно, искомое разложение имеет следующий вид

∞

∑(

(−1)n+1 3 −2)(x −1)n .

+ 2x −3

n=0

Построенное разложение имеет место в области перекрытия областей сходимости 0 < x < 2 и −3 < x < 5 , т.е. для 0 < x < 2 .

Задача 5.12. Разложить в ряд Маклорена функцию f ( x) = xe2 x +1 .

Решение. В этом примере ищется разложение функции в ряд по степеням x. Воспользуемся известным разложением

104

∞

ex = ∑

=1 +

+... +

+... .

n=0 n!

Для

этого

преобразуем

заданную

функцию

виду

f ( x) = xe 2 x +1 = xe2 x e , и в разложении e x вместо x подставим 2x:

∞

n+1

f (x) = xe2xe = xe∑(2x)

= e∑

n=0

Итак, искомое разложение функции f ( x )

имеет следующий вид

∞ 2n xn+1

f (x) =e∑n=0 n! .

Так как разложение для ex имеет место на всей числовой оси, то и построенное разложение функции f ( x) = xe2 x +1 справедливо для любого x .

Задача 5.13. Решить задачу Коши для уравнения второго порядка

y′′ − xy′ − y = 0

при начальных условиях x = 0 , y ( 0 ) = 1 , y ′ ( 0 ) = 0 . Решение. Искомое решение запишем в виде

′

′′

(n)

(0)

y (0)

y(x) = y(0) +

x +...+

+...

y′′(0)

y( n ) (0)

′

или

y( x) =1 +

+... +

... , т.к.

y(0) =

y (0)

= 0 .

Значение

′′

находим

из

заданного

уравнения

при

y (0)

x = 0 , y ( 0 ) = 1 , y ′ ( 0 ) = 0 .

Чтобы найти y′′′(0), y(4) (0),... y(n) (0),... ,последовательно дифференцируем

исходное уравнение

y ′′′ − xy ′′ − 2 y ′ = 0 ,

						′′′
						y (0) =0;
y ( 4 ) −	x y ′′′ − 3 y ′′ =		0 ,			y(4) (0) =3;
y ( 5 ) −	x y ( 4 )	− 4 y ′′′ =		0	,	y(5) (0) =0;
y ( 6 ) −	x y ( 5 )	− 5 y ( 4 )	=	0	,	y(6) (0) =1 3 5;

……………….……………………………………

105

y ( 2 k −1 ) − x y ( 2 k − 2 ) − ( 2 k − 2 ) y ( 2 k − 3 ) = 0

y ( 2 k − 1 ) ( 0 ) = 0 ;

y ( 2 k ) − x y ( 2 k −1 ) − ( 2 k − 1) y ( 2 k − 2 ) = 0 ,

y(2k ) (0) =1 2 3 ...(2k −1) ,

……………………………………………………………

(k = 2, 3, 4,...) .

Подставляя эти значения производных в разложение для искомое решение задачи Коши

y(x) =1+

+...+

+...

1 2 4

1 2 4 6

1 2 4 6 ...(2n)

∞

2 n

y ( x )

= 1 + ∑

( 2 n ) !

n =1

Вопросы для самопроверки по теме 5.2

y(x), получим

или

1.Какой ряд называют функциональным рядом?

2.Какой ряд называется вещественным?

3.Какой ряд называется комплексным?

4.Что называется областью сходимости функционального ряда?

5.В каком случае ряд называется равномерно сходящимся в промежутке

(a,b)?

6.Что можно сказать о сумме равномерно сходящегося в промежутке (a,b) ряда, если члены его непрерывны в (a,b)?

7.Можно ли почленно интегрировать и почленно дифференцировать равномерно сходящиеся ряды?

8.Сформулируйте признак Вейерштрасса равномерной сходимости функционального ряда.

9.Ряды какого вида называются степенными рядами?

10.Сформулируйте теорему Абеля.

11.Дайте определение интервала сходимости, радиуса сходимости.

12.Что называют разложением функции в ряд Тейлора?

13.Как выглядит разложение функции в ряд Тейлора?

14.Что называется разложением функции в ряд Маклорена?

15.Напишите разложение в ряд Маклорена функции ex .

16.Напишите разложение в ряд Маклорена функции 1 −1 x .

106

<<< < Предыдущая 1 2 3 4 5 67 / 137 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.04.20151.46 Mб43litology-kl-2012.pdf
#
26.08.2019890.88 Кб26LOGISTIKA_RASPREDELENIYa_Uchebnoe_posobie.doc
#
02.04.2015459.26 Кб6Marketing_Uchposobie.doc
#
25.11.20191.24 Mб7MATAN.doc
#
02.04.2015292.39 Кб54MATAN_RGZ.docx
#
02.04.20151.89 Mб62matematika.pdf
#
07.05.2019499.2 Кб7Materialy_po_teme_Pronoun_dlya_1_kursa.doc
#
14.08.2019209.58 Кб2Material_dlya_podgotovki_k_GEK_2012.docx
#
20.11.2019583.68 Кб2MathI_opor_konsp_3.doc
#
19.09.201965.02 Кб3Matved_12-15.doc
#
22.11.2019651.26 Кб4mat_ved_kp.doc