2. Функции алгебры логики

2.1. Определение и задание функций алгебры логики

Методы анализа и синтеза всех классов дискретных автоматов строят на базе алгебры логики. Начало алгебры логики было положено ирландским математиком Д. Булем (1815-1864 гг.).

Функцию f(x₁, х₂, ..., х_п) называют функцией алгебры логики (ФАЛ) или булевой функцией (БФ), если она, как и ее переменные, может принимать только два значения: 0 и 1. Переменные ФАЛ сопоставляют со значениями сигналов на входах дискретного автомата, а значения функции алгебры логики – со значениями сигналов на его выходах.

Реальные дискретные автоматы имеют конечное число входов, следовательно, число переменных у соответствующих ФАЛ также конечно. Так как переменные ФАЛ могут принимать только два значения, область определения любой ФАЛ конечна.

Существует ряд способов задания БФ.

1) При табличном способе БФ задают таблицей ее значений в зависимости от значений переменных. Например, в табл. заданы две БФ трех переменных: f(х₁, х₂, х₃) и φ(х₁, х₂, х₃).

Таблица 2.1

Совокупность значений переменных называют набором, или точкой. Каждому набору переменных, или каждой точке, соответствует определенное значение функции. При трех переменных можно образовать восемь наборов. Следовательно, приведенные в табл. 2.1 функции определены на восьми наборах (или в восьми точках). Каждый набор представляет собой трехразрядное двоичное число.

Если ФАЛ содержит n переменных, двоичные числа будут n-разрядные и, следовательно, общее число наборов будет k = 2ⁿ.

При каждом наборе переменных возможны два значения ФАЛ: 0 или 1. Поэтому в соответствие каждой ФАЛ можно поставить k-разрядное двоичное число. Значит, число функций алгебры логики n аргументов R = 2^k = 2ⁿ.

Таблицу, в которой для всех наборов переменных приводятся значения БФ, называют таблицей истинности. При n переменных таблица содержит 2ⁿ строк (по числу наборов), n столбцов (по числу переменных) и один столбец значений функции.

2) При графическом способе наборам значений переменных БФ сопоставляются точки n-мерного пространства. Вершинам куба соответствуют наборы значений переменных и приписаны значения функции на этих наборах, т.е. областью определения БФ, зависящей от п переменных, является множество вершин единичного n-мерного куба. Куб называют единичным, так как каждое его ребро соединяет вершины, наборы которых различаются одной переменной. Функции f(х₁, х₂, х₃) и φ(х₁, х₂, х₃), заданные таблицей истинности, можно задать графически (рис. 2.1).

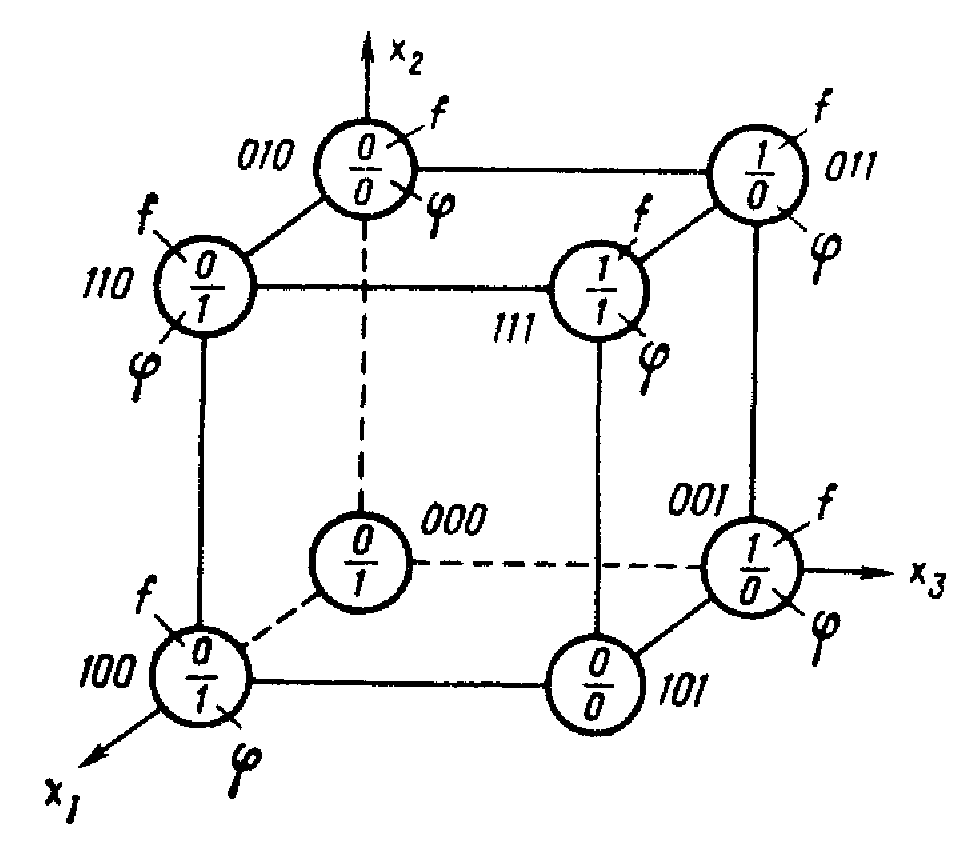
Рис. 2.1

3) При координатном способе функцию задают в виде координатной карты состояний, которую называют картой Карно.

Карты представляют собой прямоугольные таблицы, разделенные горизонтальными и вертикальными линиями на клетки. Общее число клеток соответствует числу наборов функции. Все переменные функции разбивают на две группы. Одна группа переменных определяет выбор строки, другая – столбца. На пересечении строки и столбца находится клетка, в которую записывают значение функции при соответствующем наборе переменных. Разделение переменных на группы осуществляется так, чтобы в соседних клетках наборы различались только значением одной переменной.

Карта Карно для функции f(х₁, х₂, х₃), заданной ранее таблицей истинности, имеет вид (см. рис. 2.2).

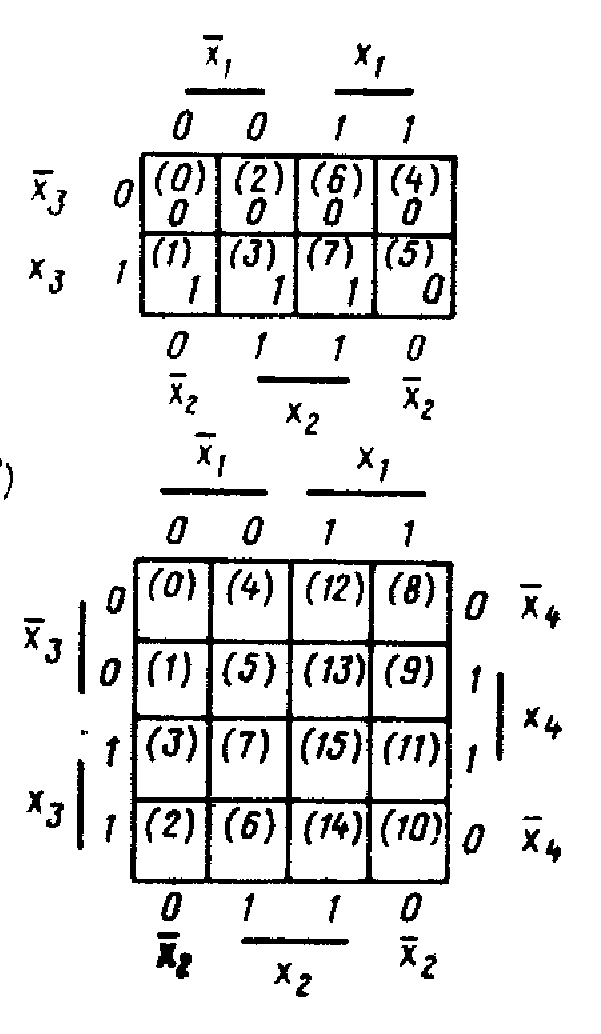
Рис. 2.2

4) При числовом способе функцию задают в виде десятичных номеров тех наборов переменных, на которых она принимает значение 1.

Функции f(х₁, х₂, х₃) и φ(х₁, х₂, х₃), приведенные в табл., могут быть заданы так:

, .

В скобках в каждой из клеток карт Карно проставлены десятичные номера соответствующих наборов.

5) При аналитическом способе функцию задают в виде алгебраического выражения, показывающего, какие и в какой последовательности должны выполняться логические операции над аргументами функции. В таблице 2.2 приведен перечень основных логических операций, используемых при записи логических выражений.

Название операции			Конъюнкция, логическое И, логическое произведение	Дизъюнкция, логическое ИЛИ, логическая сумма	Сумма по модулю два	Логическое И-НЕ, штрих Шеффера, отрицание конъюнкции	Логическое ИЛИ-НЕ, стрелка Пирса, отрицание дизъюнкции	Логическое НЕ, логическое отрицание, инверсия
Как читается			х1 и х2	х1 или х2	Или х1, или х2	х1 и х2 несовместны	Ни х1, ни х2	Не х
Таблица истинности	1	1	1	1	0	0	0	1	0
	1	0	0	1	1	1	0
	0	1	0	1	1	1	0	0	1
	0	0	0	0	0	1	1
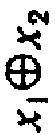
	х1	х2	х1х2	х1\/х2		х1│х2	х1↓х2	х

Алгебраическое выражение может быть составлено из наборов аргументов, на которых функция принимает значение 1, или из наборов аргументов, на которых она принимает значение 0.

Аналитические выражения для функций f(х₁, х₂, х₃) и φ(х₁, х₂, х₃), заданных таблицей истинности (см. табл. 2.1), имеют вид:

В системах железнодорожной АТС могут применяться ДУ, закон функционирования которых определен не полностью. В таких устройствах некоторые комбинации сигналов на входы никогда не подаются. Эти комбинации входных сигналов называют неиспользуемыми. Для неиспользуемых входных комбинаций выходные сигналы не определены.

Работа дискретных устройств с неиспользуемыми комбинациями входных сигналов описывается не полностью, или частично определенными функциями алгебры логики, т. е. функциями, значения которых определены не на всех наборах переменных. Если значение БФ определено на всех возможных наборах значений ее переменных, то ее называют полностью определенной.

При задании частично определенных БФ табличным, координатным и графическим способами ставят знак *, если значение функции не определено. В случае числового задания не полностью определённой функции номера неиспользуемых наборов заключают в скобки:

.