2.6. Геометрический метод минимизация функций алгебры логики

Геометрический метод минимизации основан на представлении ФАЛ на n-мерном кубе. Число вершин куба равно 2ⁿ, т. е. числу наборов для n аргументов. Длина ребер равна условной единице, ребра совмещают с координатными осями, по которым откладывают значения аргументов. Одну из вершин куба совмещают с началом координат.

Вершины куба размечают наборами аргументов. Вершины с единичным значением ФАЛ обозначают «жирными» точками. Такие вершины соответствуют конституентам ДСНФ и могут быть обозначены этими конституентами. Если «жирные» вершины являются соседними, т. е. лежат на одном ребре, то соответствующие им конституенты отличаются значением только одного аргумента. Такие конституенты склеиваются и образуют импликанту, обозначаемую общими для них (n–1) аргументами, что соответствует обозначению ребра n-мерного куба. Таким образом, две соседние «жирные» вершины заменяются на общее ребро. Считают, что ребро поглощает свои вершины. Если четыре «жирные» вершины лежат на одной грани, то они соответствуют четырем конституентам, отличающимся значениями двух аргументов. Такие конституенты также склеиваются и образуют импликанту, обозначаемую общими для четырех вершин (n–2) аргументами. На n-мерном кубе это соответствует обозначению грани куба. Считают, что грань поглощает свои ребра и вершины. Аналогично, восемь «жирных» вершин, лежащих на одном трехмерном кубе, поглощаются этим кубом. В результате получается импликанта из (n–3) аргументов, соответствующая обозначению этого куба.

В общем случае k-мерный куб поглощает все свои 2^k «жирных» вершин и соответствует импликанте из (n–k) аргументов.

Минимизация геометрическим методом заключается в следующем. Сначала путем объединения соседних «жирных» вершин находят все простые импликанты, затем из них выбирают минимальное количество, необходимое для поглощения всех «жирных» вершин. Полученные импликанты образуют МДНФ.

Пример минимизации геометрическим методом ФАЛ показан на рис. 2.9.

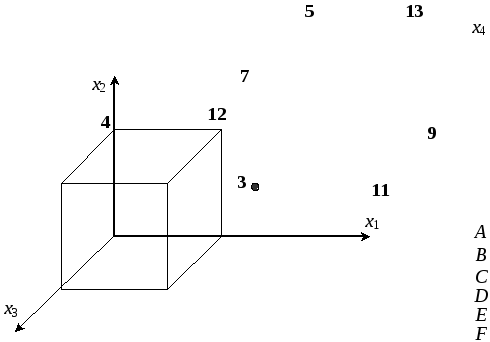
Рис. 2.9

2.7. Минимизация функций алгебры логики методом карт Карно

Метод минимизации БФ с использованием карт Карно применяют при числе переменных не более пяти. Он основан на табличном представлении значений функций. Упрощение функции табличным методом начинается с записи в клетки карты значений функции при соответствующих наборах переменных. Для заполнения карты не требуется предварительно записывать функцию в ДСНФ или КСНФ, достаточно знать наборы переменных, которым соответствуют единичные и нулевые значения функции.

Пусть условия функционирования логического автомата у = f(a,b,c,d) заданы в виде таблицы истинности (табл. 2.6).

Таблица 2.6

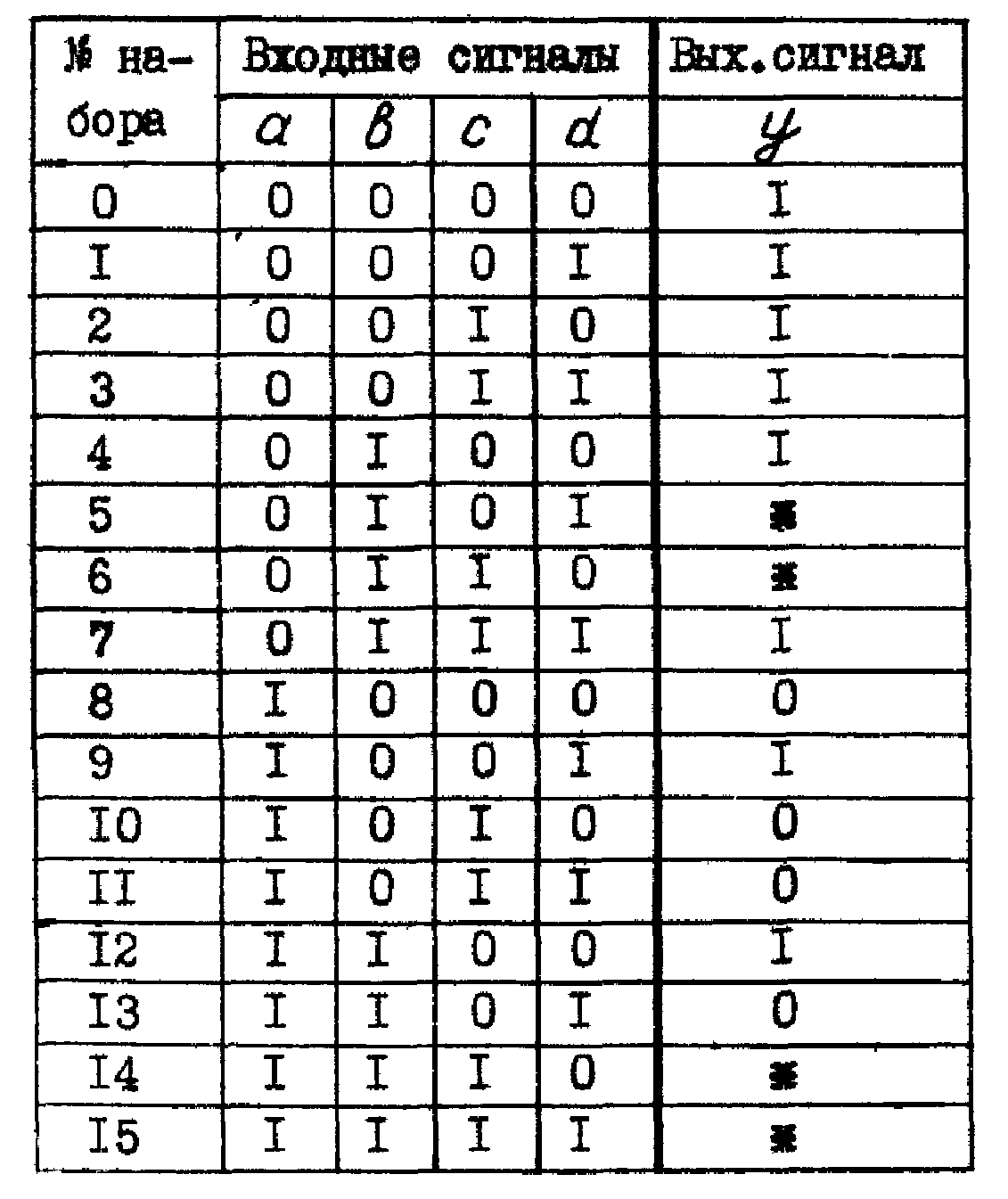
Минимизируем функцию у методом Карно, чтобы получить ее МДНФ. Для заданной функции карта Карно имеет вид (рис. 2.11):

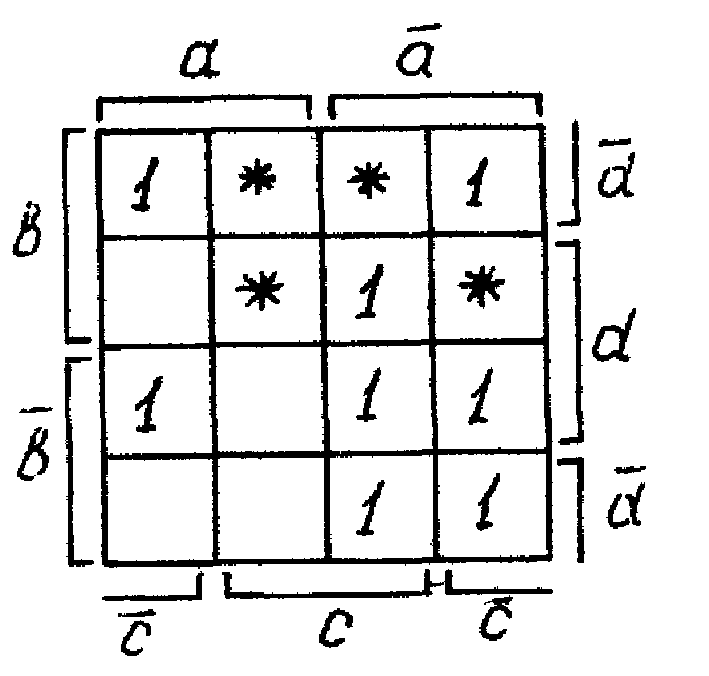
Рис. 2.11

В каждую клетку карты заносится значение функции на соответствующем этой клетке наборе значений аргументов (нулевые значения функции можно не записывать).

Если на, каком-либо наборе функция не определена, то соответствующая этому набору клетка помечается звездочкой.

Все соседние клетки, содержащие 1, нужно объединить в замкнутые контуры. При этом каждый контур должен представлять собой прямоугольник с числом клеток 2^к, где К =1, 2, 3,.... Контуры могут пересекаться, т.е. одни и те же клетки с единицами могут входить в разные контуры.

В карте Карно для n =4 (состоящих иа 2ⁿ = 16 клеток) соседними являются клетки, расположенные рядом по горизонтали и вертикали, а также клетки, находящиеся на противоположных границах карты.

При минимизации БФ методом Карно следует стремиться к тому, чтобы число контуров, охватывающих единицы карты, было минимальным, и каждый контур содержал возможно большее число клеток. При выполнении этого условия число импликант в МДНФ и число аргументов в них будут минимальными. Клетка с единицей, не вошедшая ни в один контур, обозначается всеми переменными.

Основная задача минимизации частично определенных функций заключается в отыскании оптимального варианта её доопределения, позволяющего получить минимальную из всех возможных ДНФ. При доопределении в клетки, соответствующие наборам аргументов, на которых БФ не определена, дополнительные единицы следует вписывать таким образом, чтобы контуры с уже имеющимися единицами увеличивались до максимально возможных, но при этом не образовывалось дополнительных контуров. После минимизации заданной функции, карта Карно имеет вид (рис. 2.12):

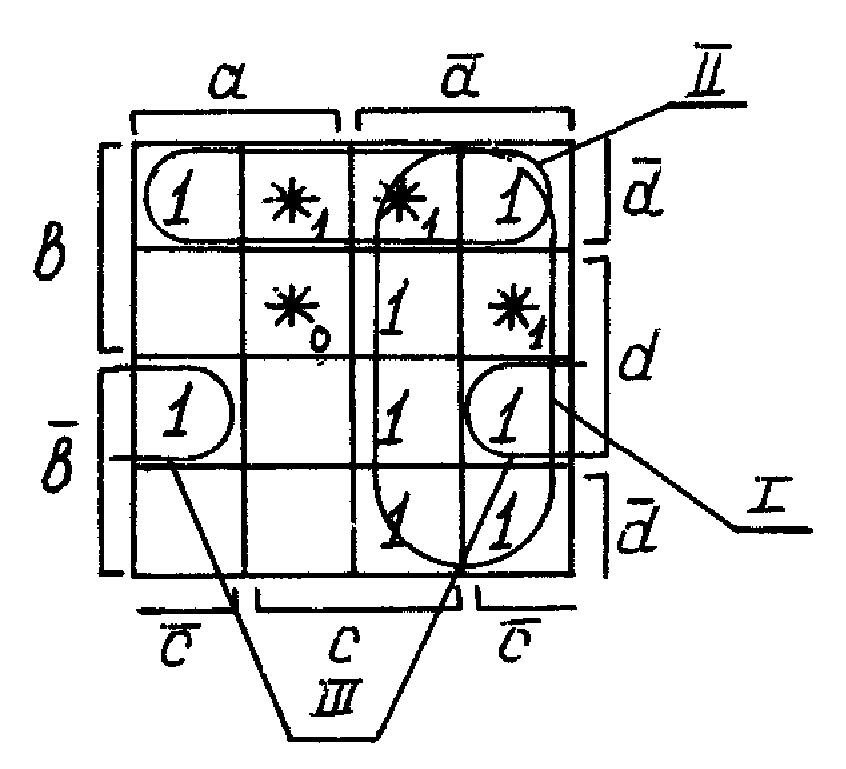
Рис. 2.12

Значения БФ, принятые при доопределении, приведены рядом со звездочками.Контур I охватывает 8 клеток, имеющих один общий аргумент (), и соответствует импликанте в МДНФ. Контур II содержит 4 клетки с 2 общими аргументами и соответствует импликанте в МДНФ. Контур III из 2 единиц соответствует импликанте из 3 аргументов. Таким образом, при минимизации мы получили МДНФ