2.5. Минимизация функций алгебры логики. Метод Квайна – Мак-Класки

Минимизация функций алгебры логики. Важной задачей является упрощение выражений для ФАЛ с целью получения такого вида формулы, при котором построенный в соответствии с ней автомат отличался бы минимальным расходом логических элементов на его изготовление (в более общей формулировке — минимальной стоимостью). Строгое решение этой задачи должно учитывать конкретные особенности логических элементов применяемой элементной базы, в частности значение коэффициента объединения и разветвления логических элементов, число элементов в корпусах и т. д. Однако существующие методы упрощения формул не решают задачу в таком объеме.

Наиболее детально разработаны методы решения канонической задачи минимизации ФАЛ, которая заключается в нахождении формы функции, содержащей минимальное число вхождений переменных. Такие формы называют минимальными.

Исходными формами функции при решении канонической задачи минимизации являются ее ДСНФ и КСНФ. Если функция задана в другой форме, последнюю преобразуют в ДСНФ или КСНФ. Рассмотрим минимизацию функций, заданных в дизъюнктивной нормальной форме.

Минимальной ДНФ (МДНФ) называют такую запись функции, которая содержит самое минимальное число переменных по сравнению со всеми другими ДНФ, эквивалентными данной функции. Существуют различные методы минимизации БФ. Все они основаны на попарном склеивании соседних конституент, отличающихся значениями только одной переменной. В одну конституенту переменная входит в прямой форме, в другую – в инверсной. Например, соседние конституенты:

и ;и.

Две соседние конституенты склеиваются по различающейся переменной, что приводит к замене их одной конъюнкцией с числом переменных, на единицу меньшим, чем в исходных конституентах:

;

.

Конъюнкции, получаемые в результате склеивания двух соседних конституент, называют импликантами. Различные импликанты с одинаковым числом переменных в свою очередь могут оказаться соседними, что позволяет склеивать их между собой: . Процесс многоступенчатого склеивания приводит к получению импликант, которые не склеиваются с другими. Такие импликанты называютсяпростыми.

Импликанта, полученная в результате склеивания некоторого множества конституент покрывает (поглощает) эти конституенты. Так, импликанта покрывает четыре исходные конституенты, каждая из которых содержит четыре переменные.

Логическую сумму всех простых импликант называют сокращенной ДНФ (СДНФ). Любая ФАЛ имеет одну СДНФ. Сокращенная ДНФ часто является избыточной, так как одна и та же конституента покрывается обычно несколькими импликантами. После исключения из СДНФ лишних импликант получают тупиковую ДНФ (ТДНФ).Последняя не содержит лишних импликант. При удалении из ТДНФ любой конъюнкции получается ДНФ, не эквивалентная исходной. К конъюнкциям ТДНФ операция склеивания неприменима.

Минимизируемая ФАЛ может иметь несколько ТДНФ. Задача состоит в выборе путем их перебора ТДНФ с минимальным числом переменных. ТДНФ, содержащая наименьшее число переменных по сравнению с другими ТДНФ, и является искомой минимальной ДНФ (МДНФ) минимизируемой БФ.

В решении задачи минимизации ФАЛ можно выделить два направления. Одно из них предполагает применение систематических методов, основанных на формализованном порядке упрощения формул. Эти методы описываются строгими алгоритмами, поддаются программированию и их применение дает возможность использовать ЭВМ, что является неизбежным при минимизации ФАЛ большого числа переменных. К таким методам минимизации ФАЛ относятся метод Квайна – Мак-Класки и метод существенных переменных.

При минимизации ФАЛ небольшого числа переменных (четыре-пять) находят применение более простые табличные методы. В этом случае процесс минимизации зависит от эвристических соображений оператора, выполняющего упрощение. Одним из таких методов является метод карт Карно.

Метод Квайна – Мак-Класки. При минимизации БФ по этому методу последовательно выполняют два этапа преобразования выражения функции: на первом переходят от канонической формы к сокращенной, на втором – от сокращенной формы логического выражения к минимальной.

Для формирования простых импликант и получения сокращенной ДНФ все конституенты минимизируемой БФ n переменных записывают в виде их двоичных номеров. Последние разбивают по числу m единиц, содержащихся в их коде, на группы. В m-ю группу войдут все номера, имеющие в своей двоичной записи ровно m единиц.

Группы двоичных номеров с одинаковым индексом располагают в столбец, разделяя их горизонтальной чертой в порядке возрастания индекса m. Далее выполняют следующие операции: попарно сравнивают двоичные номера всех членов группы с индексом m с членами группы, имеющей индекс m+1; если сравниваемые двоичные коды различаются только в одном разряде, в первый столбец остатков записывают код с прочерком на месте этого разряда; двоичные коды номеров, участвующих в операции склеивания, отмечают условным знаком, например \/. Указанные операции повторяют для всех групп последовательно в порядке возрастания m. Все не отмеченные знаком \/ двоичные номера соответствуют простым импликантам.

К полученному первому столбцу остатков с укороченными двоичными номерами вновь применяют рассмотренные операции и формируют второй столбец остатков. Склеиванию подлежат только те укороченные двоичные номера, которые содержат прочерки в одних и тех же разрядах и различаются значением только одного разряда. Во втором столбце остатков сокращенные двоичные номера будут содержать уже два прочерка.

Процесс формирования сокращенных двоичных кодов продолжается до тех пор, пока имеется возможность склеивания.

Пример. Пусть ФАЛ задана числовым способом:

.

Перейдя к двоичным эквивалентам десятичных номеров конституент, упорядочив их в группы по числу единиц и проведя операции сравнения и склеивания в соответствии с описанной выше методикой, получим:

Дальнейший процесс склеивания импликант, не отмеченных знаком дизъюнкции, невозможен. Эти импликанты являются простыми, обозначим их буквами А, В, С, D, E, F. Сокращенная ДНФ минимизируемой функции имеет вид

Дальнейшее упрощение логического выражения достигается исключением из него лишних членов.

Для составления тупиковых форм из простых импликант и получения минимальной формы используют импликантную таблицу, которую называют также таблицей покрытий. Ее строки соответствуют простым импликантам, а графы – конституентам функции (членам ДСНФ). Столбцы членов ДСНФ, при склеивании которых образована данная импликанта, отмечают метками X. Говорят, что данная импликанта покрывает (поглощает) данную конституенту. Рассматриваемой функции соответствует импликантная таблица (табл. 2.5).

Таблица 2.5

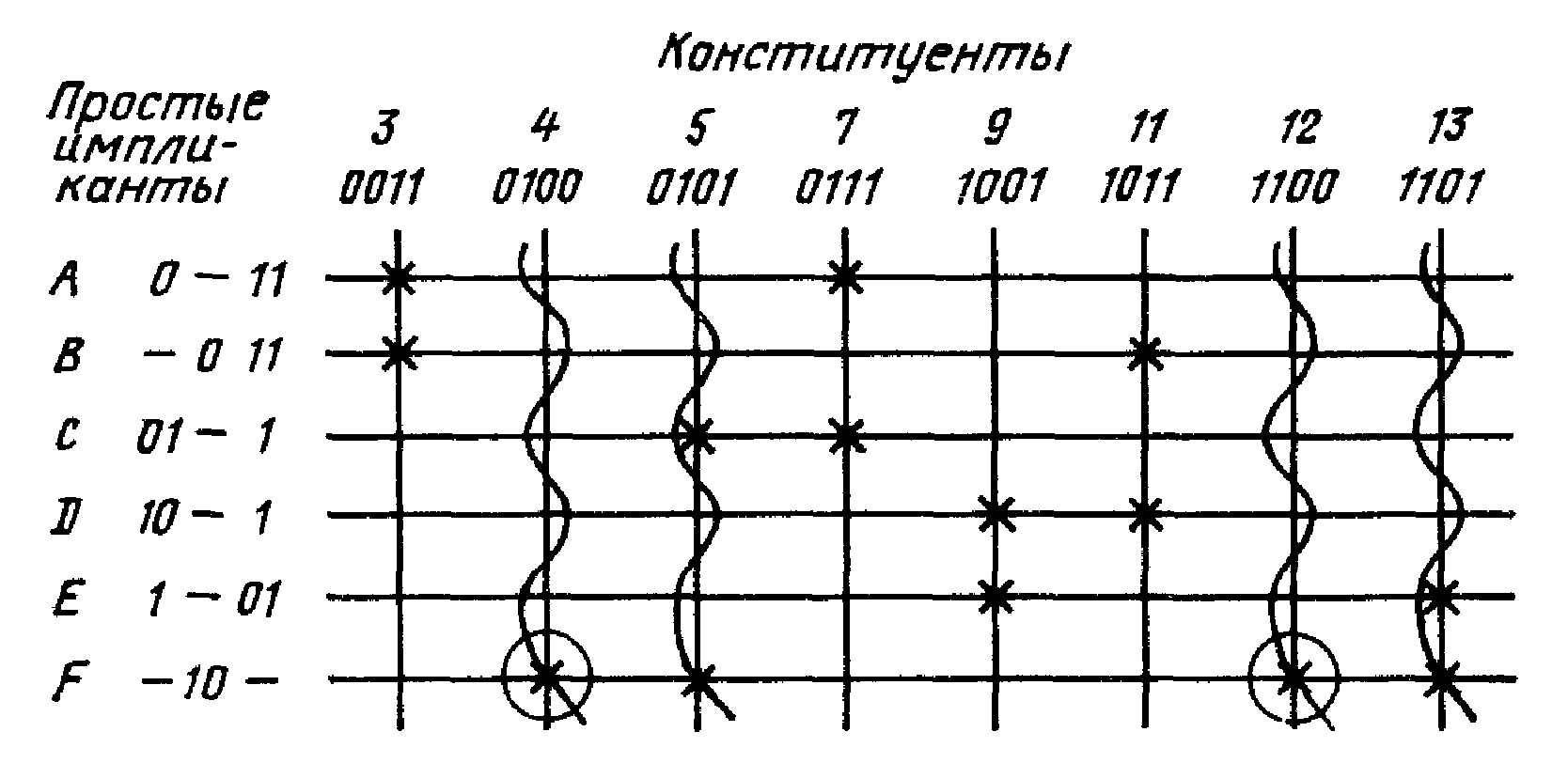
Если в каком-либо из столбцов составленной таблицы имеется только одна метка, простую импликанту, стоящую в соответствующей строке, называют существенной, и метку обводят кружком. Существенная импликанта не может быть исключена, так как без нее не будет получено покрытие всего множества конституент функции. В нашем случае существенная импликанта одна – F.

Совокупность существенных импликант называют ядром функции. После выделения существенных импликант из рассмотрения исключают (вычеркивают) те столбцы импликантной таблицы, которые соответствуют конституентам, поглощаемым существенными импликантами.

Для получения минимальной формы достаточно из импликант, не входящих в ядро, выбрать такое минимальное число их, которое включает в себя метки во всех оставшихся столбцах. При нескольких возможных вариантах такого выбора предпочтение отдается варианту покрытия с минимальным суммарным числом переменных в простых импликантах, образующих покрытие.

Для рассматриваемой функции импликанты А и D совместно покрывают все оставшиеся конституенты. Таким образом, МДНФ имеет вид

Минимальная ДНФ может быть найдена по импликантной таблице с использованием алгебраического способа. Для каждой конституенты, не поглощаемой ядром функции, записывают дизъюнкцию обозначений тех импликант, которые ее покрывают. Составляют произведение ψ этих дизъюнкций, которое называют функцией покрытий. Произведение раскрывают по правилам алгебры логики и записывают в дизъюнктивной нормальной форме. Каждый член этой формы соответствует неизбыточному набору импликант, покрывающих все конституенты заданной функции. Дизъюнкции импликант, соответствующих каждому набору совместно с ядром функции, дают тупиковые формы функции.

В соответствии с табл. 2.5 можно написать

Получились четыре тупиковых ДНФ, из которых одна минимальная, состоящая из импликант A, D и существенной импликанты F.