DKR_MatAn_2_semestr_2014

6. xy′′ = y′+ 2xy′2

В уравнении, опять-таки, отсутствует x , поэтому сделаем замену y′ = z , где z = z(x) −новая неизвестная функция, уравнение для которой имеет вид

xz′ = z + 2xz2 ; z′ = xz + 2z2 . Это уравнение Бернулли. Будем решать его методом

вариации произвольной постоянной. Решим соответствующее однородное уравнение z′ = xz : dxdz = xz ; dzz = dxx ; ∫dzz = ∫dxx + c ; ln z = ln x + ln c ;

ln z = ln cx ; z = cx.Теперь будем искать решение уравнения Бернулли по той

же формуле z = cx, считая, что в ней c = c(x) . Тогда z′ = c′x + c = cx

+ 2c2 x2

;

′

2c

2

x

2

;

x

c x + c = c +

dc

2

2

dc

dc

1

2

dx x = 2c

x

; c2

= 2xdx ; ∫c2

= ∫2xdx + c1 ; −c

= x

+ c1 ;

c = −

1

z = −

x

.

x2 + c

x2 + c

1

1

Таким образом y′ = −

x

и y = −∫

x

1

∫

d(x2 +c )

+c2

dx + c2

= −2

x2 +c 1

=

x2 + c

x2 + c

1

1

1

−12 ln x2 + c1 + c2 . Итак общее решение исходного уравнения имеет вид y = −12 ln x2 + c1 + c2 .

7. y

− y

y

−1

= 0;

y(0) =

2; y (0)

=

2

4

3

′′

′

2

Так как в уравнении отсутствует независимая переменная x , то сделаем замену y′ = z , где z = z( y) −новая неизвестная функция (то есть y становится

переменной, а z ищется как функция от y ). Тогда y′′ = ( y′x )′x = ( y′x )′y y′x = z′z и

уравнение принимает вид y4 − y3 z′z −1 = 0 ;

y3zz′ = y4 −1;

zdz

=

y4 −1

.

dy

Разделяем

y3

переменные:

y4 −1

dy ∫zdz = ∫

y4 −1

zdz =

dy + c ;

y3

y3

z2

1

y2

1

+ c;

z

2

= y

2

1

+ c1

( 2c = c1 −произвольная

=

y −

dy + c = =

+

+

2

y

3

2

2y

2

y

2

∫

постоянная);

y′2 = y2 + y12 + c1 . Из этого равенства найдем знак перед корнем и

101

k −1:

постоянную c1, используя оба начальных условия: при x = 0

22 = ±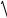2 + 12 + c1

знак «+», возводим обе части в квадрат: 12 = 2 + 12 + c1 c1 = −2 и

2

y′ =

y2 +

1

1

1

. В окрестности точки x = 0 выражение

− 2 =

y −

=

y −

2

y

y

y

y −

1

> 0, так как

y(0) −

1

=

−

1

> 0, тогда y′ = y −

1

=

y2 −1

. Опять

2

y

y(0)

y

2

y

разделяем переменные:

dy

y2 −1

;

y

= dx ; ∫

ydy

∫xdx + c ;

dx

=

dy

=

y

y2 −1

y2 −1

1

d( y2 −1)

= x + c ; ∫

d(y2 −1)

=

2x +

2c ; ln

y

2

−1

= 2x + 2c ;

y

2

−1

= e

2x

e

2c

;

2 ∫

y2 −1

y2 −1

y2 −1 = ±e2ce2 x ; y2 = c2e2 x +1; y = ±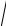c2e2x +1 . При x = 0 отсюда

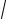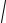2 = ±c2 +1

знак будет «+» и c2 =1 y = e2x +1– единственное решение исходной задачи Коши.

8. y′′′+ y′′−5y′+ 3y = 0; y(0) = 0; y′(0) =1; y′′(0) = −2

Уравнение является линейным однородным с постоянными коэффициентами. Его

характеристическое уравнение имеет вид k3 + k2 −5k +3 = 0 характеристический многочлен k3 + k2 −5k +3 делится на

−	k3	+ k2	−5k +3		k −1
	k3 − k2			k2 + 2k −3

−2k2 −5k

2k2 − 2k

−3k +3

−3k +3

0

Теперь решаем уравнение k2 + 2k −3 = 0 . В соответствии с теоремой Виета, его корнями являются k2 =1, k3 = −3.

Таким образом, корнями характеристического уравнения являются

k1,2 =1, k3 = −3

.Этим корням соответствует следующая фундаментальная система решений исходного дифференциального уравнения: y1 = ex , y2 = xex , y3 = e−3x общее

решение этого уравнения записывается в виде y = c1ex + c2 xex + c3e−3x . 102

Теперь найдем постоянные c1, c2 , c3 из начальных условий:

y′ = c ex			+ c	(ex + xex ) −3c e−3x						;
		1	2						3
y′′ = c ex			+ c	(ex + ex				+ xex ) + 9c e−3x . Отсюда
		1	2							3
y(0) =				c1							+c3			= 0
	′			c1				+c2		−3c3				=1 Решаем систему методом Гаусса:
y		(0) =
	′′			c1				+2c2		+9c3			= −2
y		(0) =
1 0			1			0		1 0			1		0				1
	1 1		−3			1			0 1		−4		1		= −2 ; c3			;
														8c3		= −	4
	1	2	9			−2			0 0		8		−2

c2 − 4c3 =1 c2 +1 =1; c2 = 0; c1 + c3 = 0 c1 = 14 и решение исходной задачи Коши имеет вид y = 14 ex − 14 e−3x

9. y′′+ y′− 2y =18xex

Общее решение этого уравнения имеет вид y = y + y , где y −общее решение соответствующего однородного уравнения, а y −частное решение исходного неоднородного уравнения.

Находим y : характеристическое уравнение имеет вид k2 + k − 2 = 0 ; его корни k1 = −2, k2 =1, и y = c1e−2 x + c2ex . Теперь ищем y в виде, соответствующем

правой

части Pk (x)eαx =18xex :α =1 является корнем характеристического уравнения k2 + k − 2 = 0 кратности r =1, и y следует искать в виде

y = xrQk (x)eαx = x(AX + B)ex = (AX 2 + Bx)ex . Подставим это выражение в исходное уравнение, опуская для удобства символ

: y′ = (2Ax + B)ex + (Ax2 + Bx)ex = (Ax2 + 2Ax + Bx + B)ex ;

y′′ = (2Ax + 2A + B)ex + (Ax2 + 2Ax + Bx + B)ex − 2(Ax2 + Bx)ex =18xex ;

Ax2 + 4Ax + Bx + 2A + 2B + Ax2 + 2Ax + Bx + B − 2Ax2 − 2Bx =18x .

Приравняем коэффициенты при одинаковых степенях x слева и справа:

6A =18		A = 3, 3B = −6, B = −2 y = x(3x − 2)ex и
2A +3B = 0
y = c e−2 x	+ c ex + x(3x −		2)ex	– общее решение исходного уравнения.
1	2

10. y′′+ 9y = 9x2 + xcos x + sin 3x

Характеристическое уравнение для соответствующего однородного уравнения имеет вид k2 +9 = 0 , его корни k1,2 = ±3i , и общее решение однородного

уравнения можно записать в виде y = c1 cos3x + c2 sin3x . 103

Так как правая часть исходного неоднородного уравнения есть сумма трех функций специального вида, то частное решение этого уравнения можно искать в

виде суммы y = y + y + y , где			y −частное решение уравнения	y′′+9y = 9x2	,
1	2	3	1
y −частное решение уравнения			y′′+ 9y = xcos x , y −частное решение
2			3

уравнения

y′′+ 9y = sin 3x .

Для 1ого из этих уравнений α = 0, кратность r этого α как корня характеристического уравнения k2 +9 = 0 равна 0, и y1 следует искать в виде

y1 = Ax2 + Bx + C .

Для 2ого уравнения α = 0, β =3, α + βi =3i , кратность этого числа как корня характеристического уравнения r = 0, и y2 следует искать в виде

y2 = (Dx + E)cos x + (Fx + G)sin x .

Для 3ого уравнения α = 0, β =3, α + βi =3i , кратность этого числа как корня характеристического уравнения r =1, и y3 следует искать в виде

y = x(H cos3x + I sin3x) .
3
В итоге получим общее решение исходного уравнения
y = c cos3x + c sin x + Ax2								+ Bx + C + (Dx + E)cos x + (Fx + G)sin x + x(H cos3x + I sin 3
1					2
(в этой формуле A, B, C,								D, E, F, G, H, I −неопределенные коэффициенты,
значения которых можно найти).
11. y	′′	− 4y	′	+		e2x
					5y = cos x
Характеристическое уравнение для соответствующего однородного уравнения
имеет вид k2 − 4k +5 = 0, его корни k = 2 ±									−1 = 2 ±i , и общее решение
								1,2
однородного уравнения имеет вид y = c e2 x cos x + c e2 x sin x (1).
								1	2

Так как правая часть исходного уравнения не является функцией специального вида, то для нахождения частного решения неоднородного уравнения y

применим метод вариации произвольных постоянных: будем искать y по той

же

формуле (1), считая, что в ней c1 = c1(x) , c2 = c2 (x) . Тогда для нахождения производных этх коэффициентов получим следующую систему уравнений:

′

2x

′

2x

sin x = 0

c1e

cos x + c2e

;

′

(e

2x

′

′

(e

2x

′

e2x

c1

cos x)

+ c2

sin x) =

cos x

c′cos x + c′ sin x = 0

1

2

;

′

(2e

2x

cos x

−e

2x

′

(2e

2x

sin x + e

2x

cos x) =

e2x

c1

sin x) + c2

cos x

104

c′cos x

+ c′ sin x = 0

1

2

;

′

′

(2sin x + cos x) =

1

c1(2cos x −sin x)

+ c2

cos x

c′

= −c′ cos x

c′(2cos x −sin x) −c′ cos x (2sin x + cos x) =

1

;

cos x

2

1 sin x

1

1 sin x

c′

2cos x −sin x − 2cos x + cos2 x =

1

; c′

−sin2 x −cos2 x

=

1

;

1

sin x

cos x

1

sin x

cos x

−c′

1

=

1

; c′ = − sin x

c′

= − sin x

cos x

. Теперь находим c (x) и

cos x

sin x =1

1 sin x

1

cos x

2

cos x

1

c2 (x) :

sin xdx = d cos x = ln

c (x) = −

cos x

; c (x) =

∫

dx = x .

1

∫cos x

∫

cos x

2

Значит,

y = e2x cos xln

cos x

+ xe2x sin x и общее решение исходного уравнения

y = y + y = c e2x cos x + c e2x cos x + e2x cos xln

cos x

+ xe2x sin x .

1

2

12.

y

′′

= 2xy

′

+ 4y;

′

y(0) =1; y (0) = 2

Будем искать решение этой задачи Коши в виде:

y(x)= y(x	)+	y′(x	)	(x − x	)+	y′′(x	)	(x − x	)	2		y′′′(x		)	(x − x	)	3		( )
		0				0					+	0						+...
0		1!		0		2!		0				3!			0
													(x0 )= y′(0) = 2.
По условию задачи имеем:					x0 = 0, y		(x0 )= y(0) =1, y′

y′′(0)= 2 0 2 + 4 1 = 4. Таким образом, решение исходной задачи Коши по формуле ( ) имеет вид:

y(x)= y(x0 )+ y′(1!x0 )(x − x0 )+ y′′2!(x0 )(x − x0 )2 + y′′′3!(x0 )(x − x0 )3 +... =

=1+1!2 x + 2!4 x2 +... =1+ 2x + 2x2 +....

Ответ: y(x)=1+ 2x + 2x2 +...

Замечание к задаче 12.

Если при вычислении старших производных, получаются нулевые значения y(n) (x0 ), то необходимо продифференцировать заданное уравнение и

подставить в него значения x0 , y(x0 ) и производных y′(x0 ), …, y(n−1) (x0 ), и так делать до тех пор, пока не получите 3 ненулевых члена в формуле ( ).

13. Найти кривую, у которой точка пересечения любой касательной с осью абсцисс равноудалена от точки касания и от начала координат.

Пусть y = y(x) −искомая кривая. Уравнение касательной к ней в произвольной точке (x, y) имеет вид Y − y = y′(X − x) (здесь X и Y −координаты точек касательной). Точка пересечения этой касательной с осью абсцисс имеет

105

координаты: Y = 0 X

− x = −

y

;

X = x −

y

. Расстояния от этой точки до

y′

y′

точки

касания и до начала координат соответственно равны

y

2

+ (0 − y)2

x −

− x

y′

y

y 2

2

y

y2

2

y

2

и

x −

. По условию задачи

−

+ y

=

x −

+ y

= x

−

;

y′

y′

y′

2

y′

y′

y2

+ y2

= x2 − 2xy +

y2

;

2xy

= x2

− y2 ; y′ =

2xy

. Делим числитель и

y′2

y′

y′2

y′

x2 − y2

2 y

знаменатель дроби на x2 ≠ 0 : y′ = x 2 . Решаем это (однородное) уравнение:

1− xy2

y

= u ,

y = ux , y′ = u′x + u ; u′x +u =

2u

; u′x

=

2u

−u =

2u −u +u3

= u −u3

;

1−u2

1−u2

1−u2

x

u +u3

1−u2

dx

1−u2

du

1−u2

dx

dx x =

1−u2 ;

=

x

; ∫

du = ∫

x

+ c . Разложим

u(u2 +1)

u(u2 +1)

подынтегральную дробь в правой части этого равенства на простые:

1−u2

=

A

+

Bu + D ; 1−u2 = A(u2

+1) + (Bu + D)u . Положим u = 0 1 = A .

u(u2 +1)

u

u2 +1

Приравняем коэффициенты при u2 и u в левой и правой частях:

∫

1

2u

A + B = −1 B = −2 ; D = 0 . Теперь имеем:

−

du = ln

x

+ ln

c

;

2

u

u

+1

− ∫

d(u2 +1)

u

−ln(u

2

cx

u

cx

u

ln

u

= ln

cx

;

ln

+1) = ln

; ln

= ln

;

= cx ;

u2 +1

u2 +1

u2 +1

y

yx

y

y

x

= cx;

= cx ;

= c

; x2 + y2 =

. Таким образом, решение

y2

+1

x2

+ y2

x2 + y2

c

x2

исходной задачи можно записать в виде x2 + y2 = cy .

14. Известно, что количество радиоактивного вещества, распадающегося за единицу времени, пропорционально имеющемуся в рассматриваемый момент количеству этого вещества. Пусть за 30 дней распалось 50% первоначального количества вещества. Через сколько времени останется 1% от первоначального количества вещества?

По условию задачи y′ = ky , где y(t) −количество вещества в момент времени t .

106

Решаем это уравнение с разделяющимися переменными: dydt = ky ; dyy = kdt ;

∫dy = k∫dt + c ; ln

y

= kt + c;

y

= ekt+c = ekt ec ; y = ±ec ekt , то есть y = cekt . Из

y

этой

формулы y(0) = c , то есть c −это количество вещества в начальный момент

ce30k =

c

времени. Если x −искомый момент времени, то из условия имеем:

2

;

xk

c

ce

=

100

e30k		= 1				30k = ln 1 = −ln 2
			2					2			. Делим второе уравнение на первое:
					;
	xk			1					1
e		=	100			xk	= ln	100		= −ln100 = −2ln10
x	=	2ln10				; x =	60ln10			≈ 60 2,303	= 60 3,323 ≈199,4.
30			ln 2				ln 2
										0,693

Ответ: через 200 дней.

107

План УМД на 2013/2014 уч.г.,

Юрий Львович Александров Наталья Петровна Андреева Роберт Владимирович Арутюнян Андрей Валентинович Куприн Александр Рафаилович Лакерник Аркадий Михайлович Райцин

СБОРНИК КОНТРОЛЬНЫХ РАБОТ И МЕТОДИЧЕСКИХ УКАЗАНИЙ ДЛЯ ИХ ВЫПОЛНЕНИЯ ПО ТЕМАМ

по темам

ОПРЕДЕЛЕННЫЕ И НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ.

ТЕОРИЯ ПОЛЯ. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.

для бакалавров по специальностям

210700, 230100, 230400, 210400

Подписано в печать __.__.13. Формат 60x90 1/16 Объем усл.п.л. Тираж 500 экз. Изд №___ Заказ ____

ООО «Информпресс-94». Москва, ул. Авиамоторная, д. 8а, стр. 5

108