
DKR_MatAn_2_semestr_2014
.pdf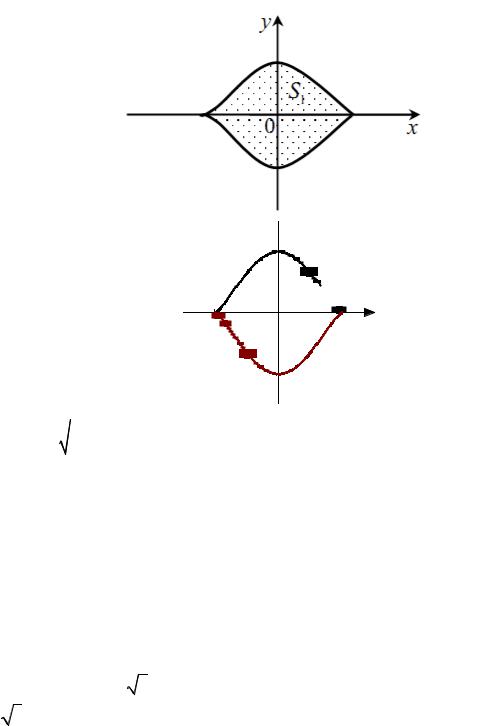
 Y
Y
S1







 X
X
0
S = 4S1 = 4∫1 |
|
dx = |
|
|
|
|
|
|
||||||
(1− x2 )3 |
|
Замена х = sint, dx = costdt |
|
= |
|
|||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
π |
|
|
|
|
|
2 |
|
Используем формулу понижения |
|
||
2 |
3 |
|
2 |
1+ cos2t |
dt = |
|
|
|||||||
|
|
|
||||||||||||
= 4∫cos |
|
t costdt =4∫ |
2 |
|
|
степени и перехода к двойному углу |
= |
|||||||
0 |
|
|
0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
= |
2 |
1+ 2cos2t + cos2 2t dt = π |
+ 2 sin 2t |
|
π |
+ |
2 |
1+ cos4tdt = |
π + 0 + 1 |
π + |
||||||||
|
||||||||||||||||||
|
2 |
|||||||||||||||||
|
∫ |
( |
|
|
|
|
|
) |
2 |
2 |
|
0 |
|
∫ |
2 |
2 |
2 |
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
2 |
||||||
+ |
1 |
|
1 sin 4t |
|
π |
= |
3π |
+ 0 = |
3π . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
02 |
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
4 |
|
|
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
2. Окружностью r = |
|
|
|
||
3sinϕ и кардиоидой r =1+ cosϕ |
|
||||
r ≤ |
|
|
|
||
3sinϕ,r ≤1+ cosϕ, т.е. нас интересует область, |
|||||
|
|
||||
лежащая внутри обеих кривых |
|
||||
51
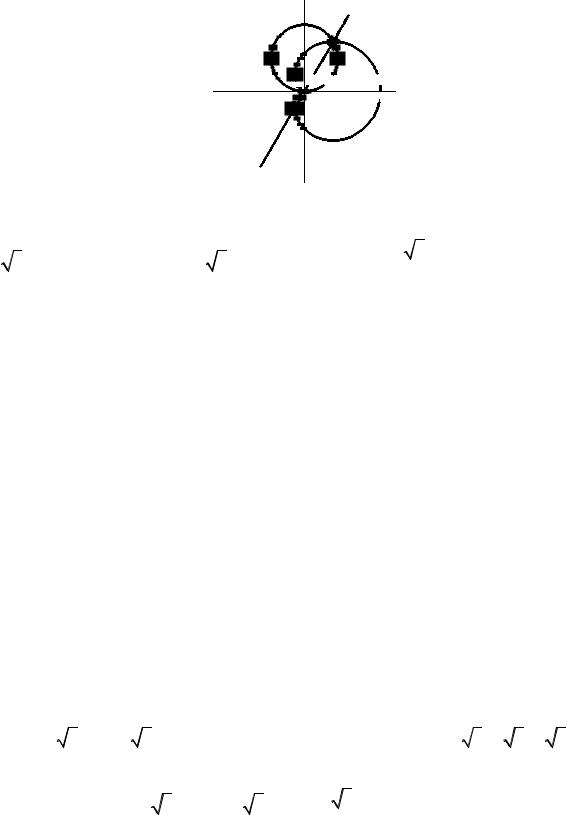
 Y
Y














 X
X  0
0


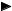
Точки пересечения кривых: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
1 cos βϕ − |
|
|
|
|
sin |
|
1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
ϕ = − |
|||||||||
|
3sinϕ =1+ cosϕ :cosϕ − |
|
3sinϕ = −1; |
||||||||||||||||||||
|
|
|
2 |
|
2 |
||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
1 |
|
|
|
|
2π |
|
|||
cos |
π |
cosϕ −sin |
π |
sinϕ = − |
; |
|
ϕ + |
π |
|
= − |
;ϕ + |
π |
= ± |
+ |
2πn |
||||||||
3 |
3 |
2 |
cos |
3 |
|
2 |
3 |
3 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ϕ= −π + 2πn, и ϕ = π3 +2πn;
ϕ= −π,−3π,−5π,π,3π,5π,.... ϕ = π3 ,π3 + 2π,π3 − 2π,...
В пределах нашего чертежа, например, при ϕ [0; 2π], ϕ = |
π |
|
и ϕ =π. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
∫3 |
|
|
|
|
|
|
|
|
|
1 |
|
π |
|
|
|
|
|
|
|
|
|
|||
Исходя из формулы S = |
∫r2dϕ, имеем: S= |
|
3sin2 ϕdϕ + |
|
∫(1+ cosϕ)2 dϕ = |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
2 |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 3 |
3 |
(1 |
−cos2ϕ)dϕ + 1 |
π |
1+ 2cosϕ + cos2 ϕ dϕ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
4 |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
∫( |
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
3 |
|
π |
|
− |
3 |
sin 2ϕ |
|
π |
|
+ |
1 |
|
|
− |
π |
+sinϕ |
|
π |
1 |
π |
(1+ cos2ϕ)dϕ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
4 |
3 |
|
8 |
|
03 |
|
|
π |
3 |
|
|
π + |
4 |
π∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
3 |
|
|
|
π |
|
|
|
|
|
|
|
|
1 |
|
|
|
π |
|
1 |
|
|
|
|
|
|
|
|
|
π |
|
π |
|
|
π |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
π − |
sin 2ϕ |
π |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|||||||||||||||||||||||||||
= |
|
− |
|
|
|
|
|
+ |
|
− |
|
|
|
|
|
|
+ |
|
|
|
|
+ |
|
π |
= |
|
|
|
|
+ |
|
|
+ |
|
|
− |
|
|
|
|
− |
|
|
|
|
− |
|
|
|
= |
||||||||||||||
4 |
|
16 |
|
3 |
|
2 |
|
|
|
3 |
8 |
|
4 |
3 |
|
6 |
16 |
|
|
2 |
|
16 |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3(π − |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
3π + 4π + 2π |
|
|
12 |
|
|
|
3π |
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
= |
− |
3 |
|
= |
− |
3 |
= |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
12 |
|
|
|
|
|
16 |
|
|
|
4 |
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x =t − t |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
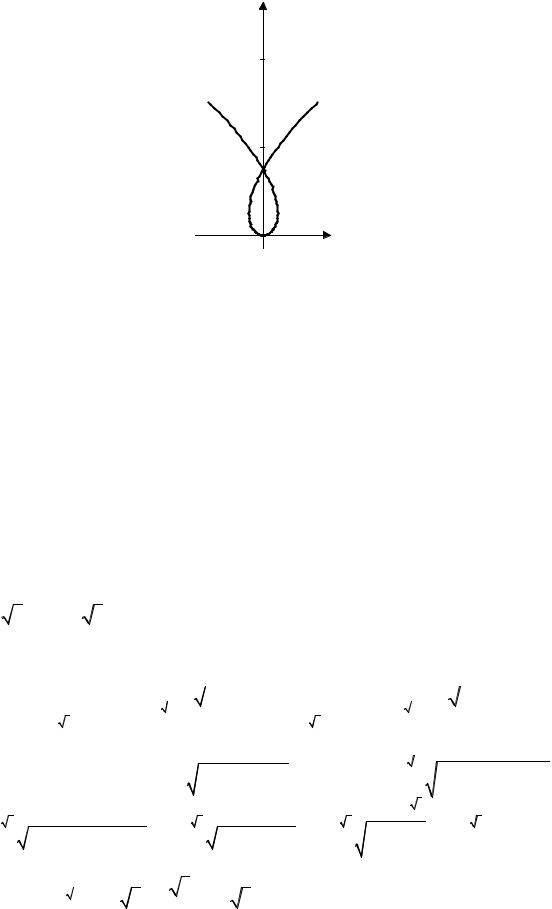
3. Вычислить длину дуги петли кривой: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
52 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
8 |
4 |
X |
0 |
Отметим, что хотя каждому значению t соответствует одна вполне определенная точка кривой, одной и той же точке кривой могут соответствовать разные значения параметра t .
Так как для двух значений t и t1 абсцисса x и ордината y в точке
самопересечения должны быть одними и теми же, то из уравнения кривой следуют два условия для t и t1
|
2 |
=t1 |
2 |
|
|
|
t |
|
|
|
|
||
|
|
|
t3 |
|
t 3 |
, причем t ≠ t1 . |
|
− |
=t − |
||||
t |
|
1 |
|
|||
|
|
|
3 |
1 |
3 |
|
|
|
|
|
|
||
Поскольку |
|
t ≠ t1 из первого уравнения следует t = −t1 . Подставляя это значение |
|||||||||||||||||||||||||||||||||
во второе уравнение, получим t − t3 |
= 0 t (3 −t2 )= 0. Если t = 0, то t1 = 0 и |
||||||||||||||||||||||||||||||||||
значения t |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
и t1 совпадают, что невозможно. Остается только одна возможность |
|||||||||||||||||||||||||||||||||||
t = |
|
|
и t = − |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Этим значениям соответствует одна и та же точка с координатами (0;3), но |
|||||||||||||||||||||||||||||||||||
угловые коэффициенты касательных различны |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
' |
|
y' |
|
|
|
|
|
|
2t |
|
|
|
|
|
|
' |
|
y' |
|
|
|
|
|
|
2t |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y x = |
|
|
t |
|
|
|
|
= |
|
|
|
|
|
|
|
|
= |
3 ; y x |
= |
t |
|
|
|
|
= |
|
|
|
|
|
|
= − 3 . |
|||
|
x' |
|
|
|
1−t2 |
|
t=− 3 |
x' |
|
|
|
|
1−t2 |
|
t= 3 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
t |
|
t=− |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
t= 3 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Через точку (0;3) кривая проходит дважды (точка самопересечения).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫3 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1−t2 )2 +( |
|
|
|
|||||||
Исходя из формулы |
|
|
|
L = ∫ |
|
(xt′)2 +(yt′)2 dt, имеем L = |
|
|
2t)2 dt = |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
∫ |
|
|
|
|
2 |
|
|
4 |
|
|
2 |
|
|
|
|
∫ |
|
|
|
|
2 |
|
4 |
|
|
∫ |
( |
2 |
) |
2 |
|
∫( |
2 |
) |
|
||||||||||
= 2 1− 2t |
+t |
+ 4t |
dt = 2 1+ 2t |
+t |
dt = 2 |
|
|
|
1+t |
|
dt = 2 1+t |
dt = |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|||||
|
|
t3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= 2 |
|
|
|
3 |
= |
2 |
3 |
|
+ |
= 4 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
t + |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
53 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Часть 2.
Решение типового варианта
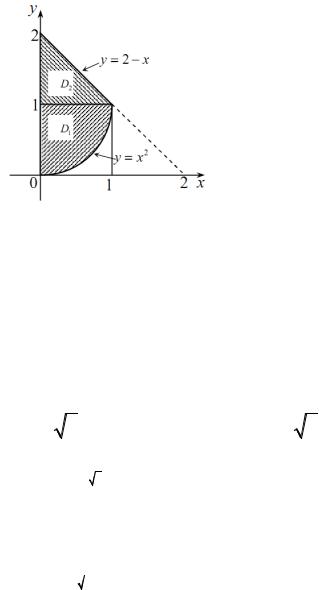
1.Расставить пределы интегрирования двумя способами в двойном интеграле ∫∫ f (x, y)dxdy в декартовых координатах для области D : y = x2 , y = 2 − x,
D
x = 0.
Решение.
I способ. При каждом значении x из отрезка [0, 1] переменная y изменяется от x2 до 2 − x , т. е. область D можно представить в виде
{ |
|
|
} |
|
|
|
|
|
|
|
|
|
|
|
D = (x, y): 0 ≤ x ≤1, x2 |
≤ y ≤ 2 − x . Тогда получаем: |
|
|
|
|
|||||||||
|
b |
y2 (x) |
1 |
|
|
2−x |
f (x, y)dy. |
|
|
|
|
|||
∫∫ f (x, y)dxdy = ∫dx |
∫ |
f (x, y)dy = ∫dx ∫ |
|
|
|
|
||||||||
D |
a |
y1(x) |
0 |
|
|
|
x2 |
|
|
|
|
|
||
II способ. При |
0 ≤ y ≤1 0 ≤ x ≤ |
|
, а при 1≤ y ≤ 2 0 ≤ x ≤ |
|
, где |
|||||||||
y |
y |
|||||||||||||
D = D1 D2 , поэтому в этом случае получаем: |
|
|
|
|
||||||||||
|
|
x2 (y) |
|
|
|
|
|
|
|
|
2−y |
|||
|
d |
1 |
|
|
|
|
y |
2 |
||||||
∫∫ f (x, y)dxdy = ∫dy |
∫ |
f (x, y)dx = ∫dy ∫ |
f (x, y)dx + ∫dy ∫ |
f (x, y)dx. |
||||||||||
D |
c |
x1(y) |
0 |
0 |
|
1 |
0 |
|
|
|
||||
Окончательно, получаем: |
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 2−x |
1 |
|
|
|
|
2 |
2−y |
|
|
|
|||
|
|
|
y |
|
|
|
||||||||
∫∫ f (x, y)dxdy =∫dx |
∫ f |
(x, y)dy = ∫dy ∫ f |
(x, y)dx + ∫dy ∫ |
f (x, y)dx. |
||||||||||
D |
0 |
x2 |
0 |
0 |
|
|
|
1 |
0 |
|
|
|
||
2. Найти массу неоднородной пластинки |
D : y = 2x − x2 , |
y = x, если |
||||||||||||
поверхностная плотность в каждой ее точке µ(x, y)= x2 + 2xy.
54
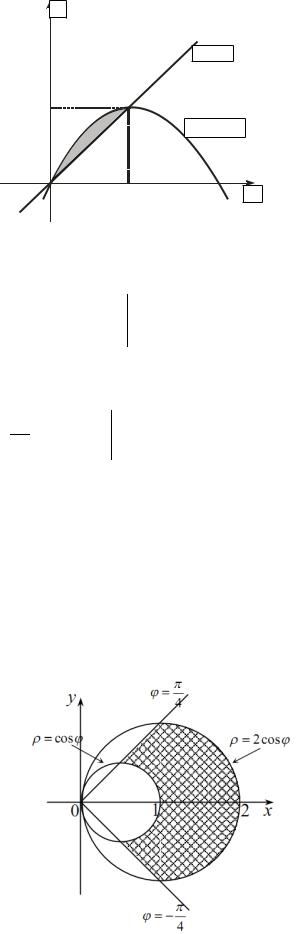
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
2 |
|
Решение: Массу неоднородной пластинки с поверхностной плотностью |
|||||||||||||||||
µ = µ(x, y) |
вычисляем по формуле |
|
m = ∫∫µ(x, y)dxdy , поэтому имеем: |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
m = ∫1 dx2x∫−x2 (x2 + 2xy)dy = ∫1 (x2 y + xy2 ) y = 2x − x2 = |
|||||||||||||||||
0 |
|
|
x |
|
|
|
|
|
0 |
|
|
|
|
y = x |
|
|
|
= ∫1 (2x3 − x4 − x3 + 4x3 − 4x4 + x5 − x3 )dx = |
|
|
|
||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
5 |
−5x |
4 |
+ 4x |
3 |
x6 |
− x |
5 |
+ x |
4 |
x =1 |
= |
1 |
. |
|||
= ∫(x |
|
|
|
)dx = |
6 |
|
|
|
|
6 |
|||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
x = 0 |
|
|
|||
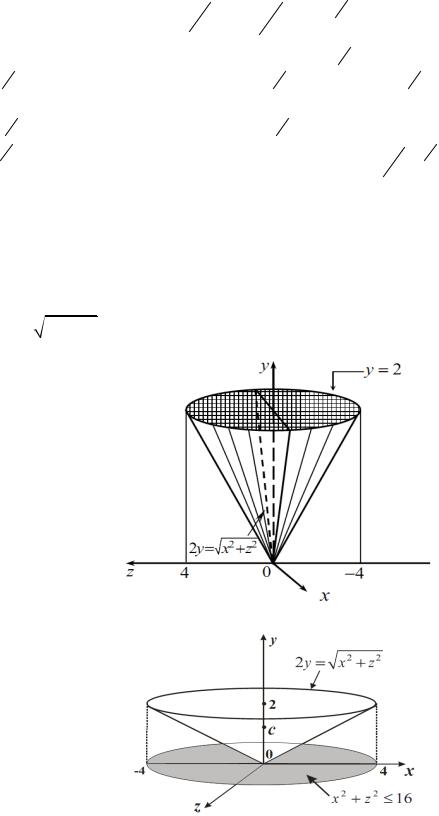
3. Найти статический момент однородной пластины D : x2 + y2 − 2x = 0, |
|||||||||||||||||
x2 + y2 − x = 0, y − x = 0, |
x + y = 0, относительно оси Oy , используя полярные |
||||||||||||||||
координаты. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение: |
Статический момент однородной пластины D (относительно оси |
||||||||||||||||
Oy) вычисляются по формулам: |
M y |
= ∫∫xdxdy (относительно оси Oy) и |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
M x = ∫∫ydxdy (относительно оси |
Ox). В данном случае имеем: |
||||||||||||||||
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
55
|
|
|
|
|
|
|
|
|
−π |
≤ϕ ≤ |
π |
|
|
π |
4 |
|
|
|
2cosϕ |
|
|
|
|
|
|
|||||
M y |
= ∫∫2ρcosϕ ρdρdϕ = |
|
4 |
|
|
|
|
4, |
|
= ∫ cosϕdϕ |
∫ |
ρ2dρ = |
|
|
|
|||||||||||||||
|
|
D′ |
|
|
|
|
|
cosϕ ≤ ρ ≤ 2cosϕ |
−π 4 |
|
cosϕ |
|
|
|
|
|
|
|
||||||||||||
|
|
π |
cosϕ (ρ3 ) |
|
ρ = 2cosϕdϕ = |
|
|
|
|
π |
|
|
π |
(1+ cos2ϕ)2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= |
1 |
∫4 |
|
2 7 |
∫4 |
cos4 ϕdϕ = |
28 |
∫4 |
dϕ = |
|
|
|||||||||||||||||||
|
3 |
−π 4 |
|
|
ρ = cosϕ |
|
|
|
3 |
|
|
−π 4 |
|
|
|
|
|
3 |
0 |
|
|
4 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
7 |
π 4 |
(1 |
+ 2cos2ϕ + cos |
2 |
2ϕ)dϕ = |
7 |
|
(ϕ +sin 2ϕ) |
|
ϕ =π |
|
π 4 |
1 |
+ |
1 |
|
|
= |
|||||||||||
|
|
|
||||||||||||||||||||||||||||
|
∫ |
|
|
|
|
|
|
4 + ∫ |
|
|
cos4ϕ dϕ |
|||||||||||||||||||
|
3 |
0 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
ϕ = 0 |
|
0 |
2 |
|
2 |
|
|
|
|
|
= |
7 |
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3 |
|
8 |
+1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4. Найти координаты центра масс однородного тела, занимающего область
V : y = 12 
 x2 + z2 , y = 2.
x2 + z2 , y = 2.
Решение:
Данное тело симметрично относительно оси Oy(Ox,Oz), поэтому xc = zc = 0,
(yc = zc = 0; xc = yc = 0), а
|
|
∫∫∫yδ (x, y, z)dxdydz |
|
|
|
|
∫∫∫xδ (x, y, z)dxdydz |
|
|
|
∫∫∫zδ (x, y, z)dxdydz |
|
y |
|
|
|
x |
= |
, z |
|
= |
|
|||
= |
V |
. |
|
V |
|
V |
|
|||||
c |
|
∫∫∫δ (x, y, z)dxdydz |
|
c |
|
∫∫∫δ (x, y, z)dxdydz |
|
c |
|
∫∫∫δ (x, y, z)dxdydz |
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
V |
|
|
|
|
V |
|
|
|
V |
|
|
|
|
|
|
|
56 |
|
|
|
|
|
|
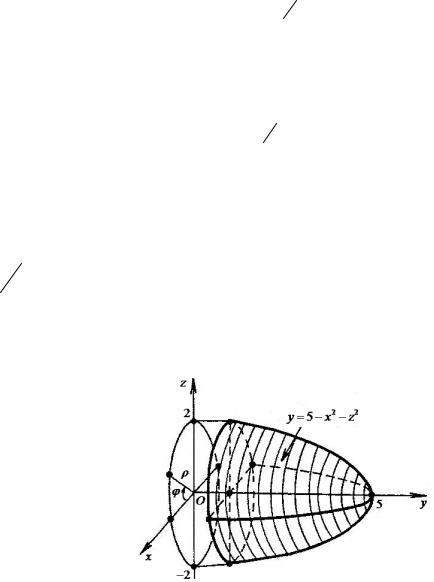
Переходя к цилиндрическим координатам по формулам |
|
x = ρcosϕ, |
||||||||||||||||||||||||||||||||||||||||
y = ρsinϕ, |
y = y, имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
4 |
|
|
|
2 |
ydy = |
1 |
2π |
|
4 |
|
|
− |
1 |
ρ |
2 |
|
|||||||
∫∫∫ydxdydz = ∫∫∫yρdρdϕdy = |
∫dϕ∫ρdρ ∫ |
2 |
∫dϕ∫ |
ρ 4 |
4 |
|
dρ = |
|||||||||||||||||||||||||||||||||||
V |
|
|
|
|
|
|
|
|
|
V ′ |
|
|
|
|
0 |
0 |
|
|
ρ |
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
1 2π |
2 |
ρ |
2 |
− |
|
ρ4 |
|
ρ |
= 4 |
dϕ = |
1 |
16ϕ |
|
|
ϕ |
= 2π |
=16π. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 ∫0 |
|
|
|
|
|
|
16 |
|
ρ |
= 0 |
|
|
2 |
|
|
|
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
4 |
|
|
|
2 |
|
|
|
2π |
4 |
|
|
|
|
|
|
|
||||||||
∫∫∫dxdydz = ∫∫∫ρdρdϕdy = |
∫dϕ∫ρdρ ∫ dy = |
∫dϕ∫ρ |
2 − |
2 |
ρ |
dρ = |
|
|||||||||||||||||||||||||||||||||||
V |
|
|
|
|
|
|
|
|
V ′ |
|
|
|
0 |
0 |
|
|
|
ρ |
2 |
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
2π |
ρ |
2 |
− |
|
ρ3 |
|
|
|
ρ = 4 |
dϕ |
= |
16 |
ϕ |
|
ϕ = |
2π |
= |
32π |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ϕ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
∫0 |
|
|
|
|
|
6 |
|
|
|
ρ = 0 |
|
|
3 |
|
|
0 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16π 3 |
|
3 |
|
|
|
|
|
|
|
|
|||||||||||||||
Следовательно, yc = ∫∫∫ydxdydz / ∫∫∫dxdydz = |
= |
и центр масс |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
V |
|
|
|
|
|
|
32π |
|
|
2 |
|
|
|
|
|
|
|
|
|||
C(0, 32,0).
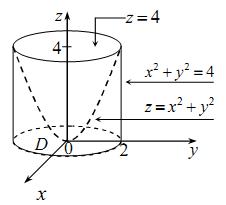
5.Найти момент инерции однородного тела относительно оси Oy ,
занимающего область V : y =5 − x2 − z2 , y =1.
Решение: Так как тело однородное, то примем δ (x, y, z)≡1, а моменты
инерции относительно осей |
Ox(Oy,Oz) будем вычислять соответственно по |
формулам: |
|
Ix = ∫∫∫δ (x, y, z)(y2 + z2 )dxdydz = ∫∫∫(y2 + z2 )dxdydz, |
|
V |
V |
Iy = ∫∫∫δ (x, y, z)(x2 + z2 )dxdydz = ∫∫∫(x2 + z2 )dxdydz, |
|
V |
V |
Iz = ∫∫∫δ (x, y, z)(x2 + y2 )dxdydz = ∫∫∫(x2 + y2 )dxdydz. |
|
V |
V |
В нашем случае, переходя к цилиндрическим координатам по формулам: x = ρcosϕ, y = ρsinϕ, y = y, имеем:
57
|
|
|
|
|
2π |
2 |
|
|
|
5−ρ2 |
|
|
|
2π |
2 |
|
y = 5 |
− ρ |
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Iy = ∫∫∫ρ2ρdρdϕdy = ∫dϕ∫ρ3dρ |
|
∫ |
dy = ∫dϕ∫y |
|
|
ρ3dρ = |
|
|||||||||||||||||||
|
V |
|
|
|
0 |
0 |
|
|
|
|
1 |
0 |
0 |
|
y =1 |
|
|
|
|
|
|
|||||
2π |
2 |
3 |
|
2 |
|
2π |
|
4 |
|
|
ρ6 |
|
ρ = 2 |
|
|
|
4 |
|
26 |
|
2π |
32π |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
= ∫dϕ∫ρ |
|
(5 − ρ |
|
−1)dρ =∫ |
ρ |
|
− |
|
|
|
|
ρ = 0 |
dϕ = 2 |
|
− |
|
|
∫dϕ = |
|
. |
||||||
|
|
|
|
|
|
|
||||||||||||||||||||
0 |
0 |
|
|
|
|
0 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
6 |
|
0 |
3 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
6. Найти объем тела, ограниченного поверхностями |
|
z = 0, |
x2 + y2 = 4, |
|||||||||||||||||||||||
z = x2 + y2.
Решение:
x2 + y2 = 4 − это круговой цилиндр радиуса 2 , ось которого совпадает с Oy.
z = x2 + y2 − параболоид, который пересекает цилиндр по окружности радиуса 2 в плоскости z = 4. z = 0 −координатная плоскость XOY . Таким образом, тело ограничено сверху параболоидом z = x2 + y2 , снизу − кругом D , а с боков
− цилиндрической |
поверхностью x2 + y2 = 4. Так как данное тело |
цилиндрическое и |
z = x2 + y2 ≥ 0, то для вычисления его объема можно |
использовать формулу V = ∫∫(x2 + y2 )dxdy, где D ={(x, y): x2 + y2 ≤ 4, z = 0}
D
− круг в плоскости XOY . Для вычисления этого интеграла перейдем к полярным координатам. При этом круг D преобразуется во множество
Dr ={(r,ϕ): 0 ≤ϕ < 2π, 0 ≤ r ≤ 2}, поэтому имеем:
V = ∫∫(r2 cos2 ϕ + r2 sin2 ϕ)rdrdϕ = 2∫π dϕ∫2 r3dr = 2π ∫2 r3dr =8π.
Dr |
|
0 0 |
0 |
|
|
y = 0, z = 0, |
|
6.1. Найти объём тела |
V : |
|
|
x + y + z = 4, |
|
||
|
|
|
|
|
|
2x + z = 4. |
|
58

Решение. Легко догадаться, что проще всего описать это тело, если
отправляться от его проекции на ось |
(x, z) D, |
Область D − |
||||||||
Oxz : V : |
||||||||||
|
|
|
|
|
0 ≤ y ≤ 4 − x − z. |
|
|
|
||
треугольник, ограниченный прямыми x = 0, z = 0, 2x + z = 4 , поэтому |
|
|
||||||||
|
2 |
4−2x |
2 |
− (4 − 2x) |
2 |
|
||||
V = ∫∫(4 − x − z)dxdz = ∫dx |
∫ (4 − x − z)dz = ∫ 16 −8x − 4x + 2x2 |
|
dx = |
|||||||
D |
0 |
0 |
|
2 |
|
|
||||
0 |
|
|
|
|||||||
= ∫2 dx(4z − xz − z2 / 2) |
|
z=4−2x = = ∫2 (8 |
− 4x)dx = (8x − 2x2 ) |
|
2 =16 −8 =8. |
|
|
|||
|
|
|
|
|||||||
|
|
|
||||||||
0 |
|
|
z=0 |
0 |
|
|
0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
7. Вычислить (непосредственно или с помощью формулы Грина): |
|
|
||||||||
∫ x2 ydx + x3dy, |
L −контур, ограниченный параболами y2 = x, |
x2 = y. |
|
|
||||||
L |
|
|
|
|
|
|
|
|
|
|
Решение:
а). Непосредственно:
Представим замкнутый контур L как сумму двух дуг L1 = x2 и L2 = 
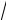 x .
x .
59

1 |
1 |
0 |
∫ x2 ydx + x3dy = ∫x2 ydx + ∫x3dy + ∫x2 ydx + ∫x3dy = ∫x4dx + ∫x3 2xdx + ∫x2 
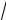 xdx +
xdx +
L |
|
|
|
|
|
|
|
L1 |
|
|
|
L1 |
|
|
L2 |
|
|
|
|
|
|
L2 |
|
|
0 |
0 |
1 |
0 |
x3 |
|
|
x5 |
|
|
|
2x5 |
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + |
|
1 + |
2x2 |
|
0 + |
x2 |
|
|
0 |
|
3 |
|
3 |
|
6 |
|
|
|
|||||
+∫ |
|
dx = |
|
|
|
|
|
|
= |
− |
= |
; |
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1 |
2 x |
5 |
|
0 |
5 |
|
0 |
7 |
|
1 |
7 |
|
1 |
|
5 |
|
7 |
|
35 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
б). По формуле Грина:
∫P(x, y)dx +Q(x, y)dy = ∫∫ |
|
∂Q − |
∂P |
|
тогда имеем |
|
|
||||||||||||||||
|
dydx , |
|
|
||||||||||||||||||||
L |
|
|
|
|
|
|
|
|
|
D |
|
∂x |
|
∂y |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
∫x2 ydx + x3dy = ∫∫(3x2 − x2 )dydx = ∫∫2x2dydx = ∫2x2 y |
|
2x dx = ∫2(x2 − x4 )dx = |
|||||||||||||||||||||
|
|||||||||||||||||||||||
x |
|||||||||||||||||||||||
L |
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
D |
0 |
|
|
0 |
|
|||
|
2 |
7 |
x5 |
|
1 |
|
2 |
|
1 |
|
|
6 |
|
|
|
|
|
|
|
|
|
||
x2 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= 2 |
|
|
|
|
= 2 |
|
− |
|
|
= |
|
. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
7 |
|
|
|
|
|
|
|
5 |
|
35 |
|
|
|
|
|
|
|
|
|
|||
|
|
5 0 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
8. Найти единичный вектор нормали к поверхности G : |
x2 + y − z2 =1 в точке |
||||||||||||||||||||||
M (1,1,1), нормаль |
образует острый угол с положительным направлением оси |
||||||||||||||||||||||
Oz.
Решение. В уравнении, задающем поверхность G , участвует функция f (x, y, z)= x2 + y − z2 −1.
Найдем координаты градиента функции f (x, y, z) в произвольной точке
M (x, y, z): |
|
|
∂f |
|
= 2x; |
|
|
∂f |
=1; ∂f |
= −2z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
∂y |
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
grad f |
= |
∂f |
|
|
|
|
|
|
∂f |
|
|
|
|
∂f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
∂x |
i |
+ |
∂y |
|
j + |
∂z |
k = 2x i |
+1 j − 2zk =(2x;1;−2z). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
∂f |
2 |
|
|
∂f |
2 |
|
∂f |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
grad f |
|
= |
|
|
|
= |
|
4x |
2 |
+1 |
+ 4z |
2 |
= |
1 |
+ 4x |
2 |
+ 4z |
2 |
. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
+ |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
∂x |
|
|
|
∂y |
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
В заданной точке M (1,1,1)= M0 |
|
|
|
координаты градиента функции |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
∂f (M0 ) |
= 2; |
|
∂f (M0 ) |
|
=1; |
|
∂f (M0 ) |
= −2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
grad f (M0 )= |
|
∂f (M |
0 |
) |
|
|
∂f (M |
0 |
) |
|
|
|
∂f |
(M |
0 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
i + |
|
|
|
|
|
|
j + |
|
|
|
|
|
|
k = 2 |
i |
+1 |
|
|
j |
− 2k = (2;1;−2). |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
∂x |
|
|
|
|
|
∂y |
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
grad f (M0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
grad f |
|
|
|
|
2 |
|
|
1 |
|
|
|
2 |
|
|
2 |
|
1 |
|
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
= |
1+ 4 + 4 =3, n |
|
= ± |
|
|
|
|
|
|
|
|
= − |
|
i − |
|
|
j + |
|
|
k = − |
|
;− |
|
; |
|
|
, |
|||||||||||||||||||||||||||||||||||
|
|
|
|
grad f |
|
3 |
3 |
3 |
3 |
3 |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
т.к. cosγ = |
2 > 0, но это означает, что нормаль к заданной поверхности G в |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
точке |
M (1,1,1) |
|
образует острый угол с положительным направлением оси Oz. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
60
