DKR_MatAn_2_semestr_2014

π

sin(ln x)dx

6

dx

1

dx

2

dx

e

∞

16xdx

1.

∫

;

2. ∫

; 3.

∫

;

4. ∫

; 5. ∫

;

1+

(

)

2

5 + 2cos x

x

16x4 −1

3x − 2

2

1

−1

0

1

1

1+ x

6.

∫1

dx

.

0 (3 − x) 1− x

II. Геометрические приложения определенных интегралов. Вычислить площадь области, ограниченной кривыми:

1.y = ln(x + 2), y = 2ln x, y = 0 .

2.Внутри окружности ρ = sinφ и одновременно вне четырёхлепестковой розы

ρ = sin2φ .

Вычислить длинудуги кривой:

3. x2 + y2 =10, внутри ветвей гиперболы xy =3.

		3
4. Найти длину дуги кривой:	x = ch t,		0 ≤t ≤π		.
				2
	y =sh3t,

Часть 2.

Кратные и криволинейные интеграла. Теория поля.

1. Расставить пределы интегрирования двумя способами в двойном интеграле ∫∫ f (x, y)dxdy в декартовых координатах для области

D

D : y = 9 − x2 , y ≥ 0, y ≥ x .

2.Найти массу неоднородной пластины D : x = 2, y = x, y =3x,если поверхностная плотность в каждой ее точке µ(x, y)= 2x2 + y2.

3.Найти статический момент однородной пластины D : x2 + y2 − 2x = 0,

y − x ≤ 0, y ≥ 0, относительно оси Ox , используя полярные координаты.

4.	Найти координаты центра масс однородного тела, занимающего область
V : x = 0, y = 0, z = 0, x + y + z =3.
5.	Найти момент инерции однородного тела относительно оси	Oz ,
занимающего область V : z = 4 x2 + y2 , z = 2.
6.	Найти объем тела, ограниченного поверхностями: z = 6 − x, z = 0,
	x2 +(y − 2)2 = 4, x2 +(y −1)2 =1.
7.	Вычислить (непосредственно или с помощью формулы Грина):
∫ y2dx +(x + y)2 dy, где L − контур треугольника ABC : A(1;0),		B(1;1),
L

C(0;1).

8.Найти единичный вектор нормали к поверхности x2 − y2 + z =1 в точке

41

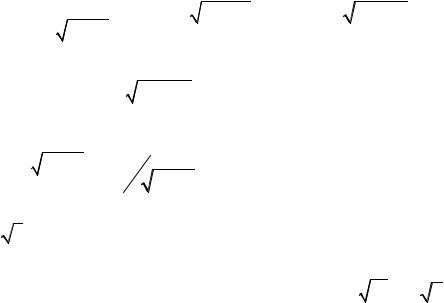
M (0,1,2), составляющую острый угол с положительным направлением оси

Oz .

9. Найти дивергенцию и ротор векторного поля F = yz2 (yzi + 2xzj +3xyk ).

Выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его скалярный или векторный потенциал и сделать проверку соответствующего потенциала.

10. Вычислить (непосредственно или по формуле Остроградского – Гаусса) поток векторного поля F =(y + z)i +(x + 6y) j + yk через внешнюю поверхность пирамиды, образуемую плоскостью x + 2y + 2z = 2 и

координатными плоскостями.
11. Вычислить (непосредственно или по формуле Стокса)					циркуляцию
векторного поля F = (3y − 2x)i + (6x − y) j + (4z − y2 −3)k					по контуру
	2	+ y	2	− z +1 = 0,
L : x
z = 2.

Вариант 27. Часть 1.

Определенные и несобственные интегралам.

I.

Вычислить интегралы:

π

3/4∫

dx

2. ∫1

dx; 3. ∫a x2

4. ∫4

dx

;

1.

;

x15

1+3x8

a2 − x2 dx;

(x +1)

2

x

x

2

+1

0

0

0

0 1+3sin

∞

dx

8

x3dx

5. ∫2

;

6. ∫0

.

x2 + x −1

64 − x2

II. Геометрические приложения определенных интегралов.

Вычислить площадь области, ограниченной кривыми:

1. y = 4 1− x2 , y =

1

.

1− x2

2. Внутриокружности ρ = 2(sinϕ −сosϕ) и одновременно вне окружности

ρ =

.

6

Вычислить длинудуги кривой:

3. Вычислить длину дуги той части кривой y = 2

− 1

x3

, которая

x

3

2

x =1 и x = 4.

расположена в вертикальной полосе, ограниченной прямыми

4. Найти длину дуги кривой

r = aebϕ (a,b > 0), находящейся внутри

окружности r = a.

42

Часть 2.

Кратные и криволинейные интеграла. Теория поля.

1. Расставить пределы интегрирования двумя способами в двойном интеграле ∫∫ f (x, y)dxdy в декартовых координатах для области

D

D : x + 2y −6 = 0, y = x, y ≥ 0.

2. Найти массу неоднородной пластины D : y = x, y = x2 , если поверхностная плотность в каждой ее точке µ(x, y)= 2x +3y.

3. Найти статический момент однородной пластины D : x2 + y2 − 2x = 0,

y − x ≤ 0, x + y ≥ 0,относительно оси Oy , используя полярные координаты. 4. Найти координаты центра масс однородного тела, занимающего область

V : z = 2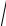x2 + y2 , x2 + y2 =9, z = 0.

5. Найти момент инерции однородного тела относительно оси Oz , занимающего область V : z =3(x2 + y2 ), z = 3.

6. Найти объем тела, ограниченного поверхностями: z = x2 + y2 , z = 0, y = 2, y = 2x, y = 6 − x.

7. Вычислить (непосредственно или с помощью формулы Грина): ∫	dx − dy	,
L	x + y
где L − квадрат ABCD : A(1;0), B(0;1), C (−1;0), D(0;−1).

8. Найти единичный вектор нормали к поверхности x2 − y − 2z2 =1 в точке M (1,−2,1),составляющую острый угол с положительным направлением оси

Oz .

9. Найти дивергенцию и ротор векторного поля

F = 2x(x(y − z)i +(−y2 )j + z2k ).

Выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его скалярный или векторный потенциал и сделать проверку соответствующего потенциала.

10. Вычислить (непосредственно или по формуле Остроградского – Гаусса) поток векторного поляF =(2y − z)i +(x + 2y) j + yk через внешнюю поверхность пирамиды, образуемую плоскостью x +3y + 2z = 6 и

координатными плоскостями.
11. Вычислить (непосредственно или по формуле Стокса)									циркуляцию
векторного поля					F = (y −3x)i			+ (7x + y) j + (2xy +3z − 4)k	по контуру
	2		2			2
L : x		+ y		= (z +1)			,
z = 0.

43

Вариант 28. Часть 1.

Определенные и несобственные интегралам.

I. Вычислить интегралы:

π

1. ∫1

ex dx

; 2. ∫2

x2 −1

dx;

3. ∫3 tg4 xdx;

4. ∫2

e1/ xdx

; 5.

∞∫

dx

;

2

2

− 4x

+ 24

0

e

+ e

1

x

π

1

x

−∞ x

6

6. ∫6

dx

.

3 (4 − x)

2

2

II. Геометрические приложения определенных интегралов.

Вычислить площадь области, ограниченной кривыми:

1. y

=

2

2)2

, y = 1

2

−5x .

(x +

2. Внутри кардиоиды ρ =1+ cosφ и одновременно вне окружности ρ = (1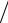3)sinφ. Вычислить длинудуги кривой:

3. y = arccosx − x − x2 , a > 0, 0 ≤ x ≤1.

	x =1−cos2t,
4. Найти длину дуги кривой:		1		0 ≤t ≤π		.
					2
	y =sint −	3	sin3t,

Часть 2.

Кратные и криволинейные интеграла. Теория поля.

1. Расставить пределы интегрирования двумя способами в двойном интеграле ∫∫ f (x, y)dxdy в декартовых координатах для области

D

D : y = −x, 2x + y = 3, y =3.

2.Найти массу неоднородной пластины D : x = 0, x + 2y + 2 = 0, x + y =1,если поверхностная плотность в каждой ее точке µ(x, y)= x2.

3.Найти статический момент однородной пластины D : x2 + y2 − 2y = 0,

y − x ≥ 0, x + y ≥ 0, относительно оси Ox , используя полярные координаты. 4. Найти координаты центра масс однородного тела, занимающего область

V : 2z = x2 + y2 , z = 3.

5. Найти момент инерции однородного тела относительно оси Ox , занимающего область V : x = 2y2 + z2 , x = 2.

6. Найти объем тела, ограниченного поверхностями: z2 = x2 + y2 , 2 z2 = x2 + y2 +1.

44

7. Вычислить (непосредственно или с помощью формулы Грина):

∫(x − y)2 dx +(x + y)2 dy, где L − контур треугольника ABC : A(0,0), B(1,0),

L

C(1,1).

8.Найти единичный вектор нормали к поверхности x2 − y2 − z =1 в точке M (2,1,2), составляющую острый угол с положительным направлением оси

Oz .

9. Найти дивергенцию и ротор векторного поля F = z(yzi + xzj + 2xyk ).

Выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его скалярный или векторный потенциал и сделать проверку соответствующего потенциала.

10. Вычислить (непосредственно или по формуле Остроградского – Гаусса) поток векторного поля F =(y + z)i + xj +(y − 2z)k через внешнюю поверхность пирамиды, образуемую плоскостью 2x + 2y + z = 2 и

координатными плоскостями.

11. Вычислить (непосредственно или по формуле Стокса) циркуляцию

векторного поля

F = (2y − x)i + (3x + 4y) j + (2xy − 2z −1)k

по контуру

2

2

2

L : x

+ y

= (z −3)

,

z = 4.

Вариант 29.

Часть 1.

Определенные и несобственные интегралам.

I.

Вычислить интегралы:

π

)

2

5

1

1

−

x

2

2

e

x

π

xsin xdx

∞ 1

+ 2x

dx

1. ∫cos

xdx; 2.

∫

dx;

3. ∫

dx;

4. ∫

;

5. ∫

(

;

x

2

x

2

(1+ x)

2

0

1 e

−1

0

1+ cos

x

1

x

2

2

2

6.

e∫

dx

.

1 x

ln x

II. Геометрические приложения определенных интегралов. Вычислить площадь области, ограниченной кривыми:

1.y = xe2x , y = xe−2 .

2.Внутри окружности ρ = 3/2 и одновременно вне кардиоиды ρ =3(1−cosφ). Вычислить длинудуги кривой:

3. y =1/sin 2x ,	π	6	≤ x ≤π	3	.

45

				a
4. Найти длину петли кривой:			ρ =		.
				cos4 (ϕ 4 )
			Часть 2.
		Кратные и криволинейные интеграла. Теория поля.
1.	Расставить пределы интегрирования двумя способами в двойном интеграле
	∫∫ f (x, y)dxdy в декартовых координатах для области D : x ≥ 0, y =1, y = −1,
	D
y = log1		x .
		2
2.	Найти массу неоднородной пластины D : x = 0, y = 0,					x + 2y =1, если
поверхностная плотность в каждой ее точке µ(x, y)= 2 −(x2 + y2 ).
3.	Найти статический момент однородной пластины D :					x2 + y2 + 2x = 0,

x + y ≤ 0, y − x ≥ 0, относительно оси Oy , используя полярные координаты.

4.	Найти координаты центра масс однородного тела, занимающего область
V : z = x2 + y2 , z = 4.
5.	Найти момент инерции однородного тела относительно оси	Oy ,
занимающего область V : y =3(x2 + z2 ), y = 3.
6.	Найти объем тела, ограниченного поверхностями: z = −x2 + 2,	z = 0, y = x,
y = 2x, x ≥ 0, y ≥ 0.
7.	Вычислить (непосредственно или с помощью формулы Грина):

∫(x2 − y2 )dx + 2xydy , где L − контур треугольника ABC : A(1;1), B(3;1),

L

C(3;3).

8.Найти единичный вектор нормали к поверхности −4x + y2 + 2z2 = −1 в точке M (1,1,−1), составляющую острый угол с положительным направлением

оси Oz .

9. Найти дивергенцию и ротор векторного поля F = x2 (xi −3yj ).

Выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его скалярный или векторный потенциал и сделать проверку соответствующего потенциала.

10. Вычислить (непосредственно или по формуле Остроградского – Гаусса) поток векторного поля F =(x + z)i + zj +(2x − y)k через внешнюю поверхность пирамиды, образуемую плоскостью 3x + 2y + z = 6 и координатными плоскостями.

46

11. Вычислить (непосредственно или по формуле Стокса)									циркуляцию
векторного поля						F = (x + y)i + (4x −5y) j + (x2 +5z + 2)k			по контуру
		2		2			2
L :	x		+ y		= (z + 2)			,
	z = −1.

Вариант 30. Часть 1.

Определенные и несобственные интегралам.

I.

Вычислить интегралы:

ln 5 ex

2

2π

2

∞

ex + 2

2

1+ x

dx

2

ln x

1.

∫

e

x

dx; 2. ∫

1− x

dx;

3. ∫

;

4.

∫x

ln xdx;

5. ∫

dx;

+3

5 −3cos x

1

+ x

2

0

0

0

1

0

6.

π∫xln(sin x)dx.

0

II. Геометрические приложения определенных интегралов.

Вычислить площадь области, ограниченной кривыми:

1.

y = arcsin x,

y = arctg2x .

2. Внутри кардиоиды ρ =3(1+ cosφ) и одновременно внутри кардиоиды

ρ =1−cosφ.

Вычислить длинудуги кривой:

3. Вычислить длину дуги той части кривой y = 56 5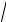x6 −165 5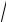x4 , которая расположена в вертикальной полосе, ограниченной прямыми x =1 и x =32.

4.Вычислить длину дуги кардиоиды ρ = 2(1+ cosφ), находящейся внутри окружности ρ =1.

Часть 2.

Кратные и криволинейные интеграла. Теория поля.

1. Расставить пределы интегрирования двумя способами в двойном интеграле

	∫∫ f (x, y)dxdy в декартовых координатах для области D : x ≥ 0, y ≥ 0, y =1,
	D
x = 4 − y2 .
2.	Найти массу неоднородной пластины D : x = 0, y = 0,			x + y = 2, если
поверхностная плотность в каждой ее точке µ(x, y)= x2 + y2.
3.	Найти статический момент однородной пластины D :			x2 + y2 + 2y = 0,

y − x ≤ 0, x + y ≤ 0, относительно оси Ox , используя полярные координаты. 4. Найти координаты центра масс однородного тела, занимающего область

V : z = x2 + y2 , x2 + y2 = 4, z = 0.

47

5. Найти момент инерции однородного тела относительно оси Oz , занимающего область V : z =3 − x2 − y2 , z = 0.

6. Найти объем тела, ограниченного поверхностями: z = x2 + y2 +1,

z = 3 − x2 − y2 .

7. Вычислить (непосредственно или с помощью формулы Грина):

∫(x + y)2 dx +(x − y)2 dy, где L − контур треугольника ABC : A(0,0), B(2,2),

L

C(4,0).

8.Найти единичный вектор нормали к поверхности 3x2 − y2 + z =1 в точке M (1,−1,−1),составляющую острый угол с положительным направлением оси

Oz .

9. Найти дивергенцию и ротор векторного поля F = 2xyz(yzi + xzj + xyk ).

Выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его скалярный или векторный потенциал и сделать проверку соответствующего потенциала.

10. Вычислить (непосредственно или по формуле Остроградского – Гаусса) поток векторного поля F = zi +(x + y) j + yk через внешнюю поверхность пирамиды, образуемую плоскостью 2x + y + 2z = 2 и координатными

плоскостями.
11. Вычислить (непосредственно или по формуле Стокса)								циркуляцию
векторного поля					F = (2x − y)i + (6x +5y) j + (3y2 −6z −1)k			по контуру
	2		2			2
L : x		+ y		= (z +3)			,
z = −4.

48

2. Решение типового варианта

Часть 1.

I. Вычислить интегралы:

x2 + x −1

A

B

C

;

=

+

+

x(x −1)(x +1)

x

x −1

x +1

x2 + x −1 =

4

x

2

+ x −1

4

x

2

+ x −1

= A(x −1)(x +1)+ Bx(x +1)+Cx(x −1)

1. ∫2

dx = ∫2

dx =

x = 0: −1 = −A; A =1

=

x3 − x

x(x −1)(x +1)

x =1: 1 = 2B; B =

1

2

1

x = −1: −1 = 2C; C = −

4

4

d (x −1)

4

d (x +1)

2

=

dx +

1

−

1

= ln

x

24 + 1 ln

x −1

24

−

1 ln

x +1

24 =

∫2 x

2

∫2

x −1

2

∫2

x +1

2

2

= ln 4 −ln 2 +

1 ln3

− 1 ln5 + 1 ln3 = ln 4 −ln 2 + ln3

−

1 ln5 = ln

6

.

2

2

2

2

5

π

2.

∫4

xtg2 xdx =

Пусть х =и => dx = du,

tg2 xdx = dv v = ∫tg2 xdx =

0

π

1

−cos2 x

dx

π

4

= x(tgx − x)

− ∫(tgx − x)dx =

= ∫

2

dx = ∫

− ∫dx =tgx − x

04

cos

x

cos

2

x

0

π

π

π

4 d cos x

x2

π

π

π2

π

π

2

=

1−

+

∫0

cos x

+

04

=

−

+ ln

cos x

04

+

=

4

4

2

4

16

32

π

π2

π

π2

1

=

−

+ ln

2

=

−

−

ln 2.

4

32

2

4

32

2

1

1

Сделаем замену

2

dx

2

t

−

dt

2

dt

t

2

3. ∫

=

1

= ∫

= −∫

=

x

2

1

1

1

x x

+8x − 2

= t

3

+

8 − 2

3 t

+ 8

− 2

3

t2

t

t2

t

= ∫3

dt

=

1

∫3

dt

=

1

∫3

d (t − 2)

=

1+8t − 2t

2

2

1

+ 4t −t2

2

9

−(t − 2)2

2

2

2

(t − 2)

2

2

1

1

2

=

arcsin

3

=

arcsin

2

.

3

2

3

2

2

49

Отметим, что при замене переменной меняются пределы интегрирования,

и возвращаться к исходной переменной не нужно.

π

Сделаем замену

tg

x

=t,

2

dx

2

4.

∫

=

=

5 −

2sin x +3cos x

sin x =

2t

,cos x =

1−t

2

,dx

=

2dt

0

2

1+t2

1+t2

1+t2

1

dt

1

dt

1

dt

1

d (t −1)

1+t

2

= ∫

= 2∫

= ∫

= ∫

=

4t

3

−3t

2

2t

2

− 4t

+8

t

2

− 2t + 4

2

+

3

0

5 −

+

0

0

0 (t −1)

1

+t2

1+t2

1

t −1

1

1

1

π

=

arctg

0

= −

arctg

−

=

.

3

3

3

3

6 3

+∞

5. Вычислить несобственный интеграл первого рода

∫е

dx

.

xln xln2 ln x

е

+∞

dx

+∞

d ln x

+∞ d lnln x

1

+∞

∫е

=

∫e

= ∫e ln2 ln x

= −

ee

= 0 +1 =1.

xln xln2 ln x

ln xln2 ln x

lnln x

е

e

e

Здесь мы использовали справедливость формулы Ньютона-Лейбница для несобственных интегралов.

6. Вычислить несобственный интеграл второго рода ∫4

dx

.

16 − x

2

0

При

x = 4

подынтегральная функция терпит разрыв, поэтому:

4

dx

4−ε

dx

4−ε

dx

x 4 −ε

∫

= limε→0

∫

= limε→0 ∫

= limε→0 arcsin

0

=

4

16 − x

2

16 − x

2

4

2

− x

2

0

0

0

ε

π

интеграл сходится.

= lim arcsin 1−

4

− arcsin0 = arcsin1 =

2

ε→0

II. Вычислить площадь области, ограниченной кривыми:

	2		(		2	)	3		(		2	)	3		2
1. y		=	1	− x				; y = ± 1		− x				Область определения х		≤1,	х	≤1;

кривая симметрична относительно обеих координатных осей.

50