DKR_MatAn_2_semestr_2014

Ответ: единичный

вектор

нормали

в

точке M (1,1,1) к поверхности

x

2

+ y − z

2

=1

0

= −

2

1

2

имеет вид n

3

i −

3

j +

3

k.

9.1. Найти дивергенцию и ротор векторного поля

F

= (2 − x2 y)i

+ y2 zj

+ (2xyz − z2 y)k.

Выяснить, является ли данное поле потенциальным или соленоидальным; если

да, то найти соответственно его скалярный или векторный потенциал и сделать

проверку соответствующего потенциала.

Решение:

1-ый способ. Вычислим divF и rotF :

∂P

+

∂Q

+

∂R

= −2xy + 2yz + 2xy − 2zy = 0.

divF =

∂x

∂y

∂z

F =

i

j

k

=(2xz − z2 − y2 )i +(2yz) j +(x2 )k ≠ 0.

rot

∂

∂

∂

∂x

∂y

∂z

2 − x2 y

y2 z

2xyz − z2 y

rota ≠

0

,

существует векторный потенциал

Имеем:

0

diva ≡

(x, y, z) j + R (x, y, z)k

b (M )= P

(x, y, z)i

+Q

, для которого имеет место

1

1

1

равенство:

rotb

(M ) = F.

Вычисление векторного потенциала. F = (2 − x2 y)i + y2 zj + (2xyz − z2 y)k.

Будем всегда предполагать, что:

P1 ≡ 0, а Q1

и R1

вычислять по формулам:

P1 = 0,

Q1 = ∫R(x, y, z)dx = ∫(2xyz − z2 y)dx = x2 yz − xyz2 ,

R =

∂

Q(x, y, z)dx +

∂

R(x, y, z)dx + P(x, y, z)

dy −

Q(x, y, z)dx =

∫ ∂y ∫

∂z ∫

∫

1

∂

(y2 z)dx +

∂

(

=

∫

∫

∫

−

∫

y2 zdx =

∂y

∂z

2xyz − z2 y)dx + 2 − x2 y dy

= ∫

2xyz + x

2

y − 2xyz

+ 2 − x

2

2

z = 2y − xy

2

z.

y dy − xy

Следовательно,

b

(M )= b (x, y, x)=(x2 yz − xyz2 )j +(2y − xy2 z)k.

Проверка:

rot b

(M ) = F.

61

rotb (M )=

i

j

k

∂

∂

∂

=

∂x

∂y

∂z

0

x2 yz − xyz2

2y − xy2 z

=(2 − 2xyz

− x2 y + 2xyz)i −(−y2 z)

j +(2xyz − yz2 )k =

=(2 − x2 y)i +(y2 z)j +(2xyz − yz2 )k = F.

Известно, что векторный потенциал вычисляется с точностью

f −

grad f , где

произвольная функция, поэтому окончательно имеем:

b (M )=(x2 yz − xyz2 )j +(2y − xy2 z)k

+ grad f .

2-ый способ.

Векторный

потенциал

поля

F

определяется

с

точностью

до градиента

произвольной

дифференцируемой

функции:

где

b1

(M )=b2 (M )

+ grad f ,

b (M )

и b

(M ) – два векторных потенциала одного и того же поля F .

1

2

Этим обстоятельством пользуются при отыскании векторного

потенциала. А именно, полагают одну из компонент поля b равной нулю.

Пусть, для определенности P

(x, y, z)≡ 0., тогда из равенства F = rotb или, в

1

i

j

k

∂

∂

∂

подробной записи, Pi +Qj + Rk =

следует, что

∂x

∂y

∂z

0

Q1

R1

∂R1 − ∂Q1

= P,

∂R1

= −Q,

∂Q1

= R.

∂y

∂z

∂x

∂x

F .

Интегрируя эту систему, получаем некоторый потенциал b1

данного поля

(M )

Общее решение имеет вид b

=b1

(M )+ grad f , где f – произвольная

дифференцируемая функция.

F = (2 − x2 y)i

+ y2 zj + (2xyz − z2 y)k.

Из 1 способа имеем:

∂P

+

∂Q

+

∂R

= −2xy +

2yz + 2xy − 2zy = 0.

divF =

∂x

∂y

∂z

rotF =

(2xz − z2 − y2 )i +(2yz)

j +(x2 )k

≠ 0.

Т.к. P1 (x, y, z)≡ 0

∂R1 = −Q ∂R = −Q∂x R = −xy2 z + F (y, z)

∂x

1

1

1

62

∂∂Qx1 = R ∂Q1 = R∂x Q1 = x2 yz − yz2 x + F2 (y, z).

А теперь используем равенство: ∂∂Ry1 − ∂∂Qz1 = P = 2 − x2 y

−2xyz + ∂F1	−x2 y +2xyz − ∂F2 = 2 −x2 y , т.е					∂F1	− ∂F2	= 2 . Положим теперь
∂y		∂F1		∂z		∂y	∂z
F (y, z) ≡ 0,	тогда			= 2 или F (y, z) = 2y,		поэтому
2		∂y		1
R = −xy2 z + F (y, z)= 2y − xy2 z.
1	1
Следовательно, векторный потенциал данного поля равен:
b (M )=(x2 yz − xyz2 )j				+(2y − xy2 z)k	+ grad f .

Итак, векторный потенциал вычислен двумя способами и получен один и тот же ответ.

9.2. Найти дивергенцию и ротор векторного поля

F = (2xy + z)i + (x2 − 2y) j + xk.

Выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его скалярный или векторный потенциал и сделать проверку соответствующего потенциала.

∂P

+

∂Q

+

∂R

= 2y − 2 ≠ 0.

Решение: divF =

∂x

∂y

∂z

i

j

k

i

j

k

∂

∂

∂

∂

∂

∂

rotF

=

=

= 0

i + (1

−1) j

+ (2x − 2x)k ≡

0.

∂x

∂y

∂z

∂x

∂y

∂z

P Q R

2xy + z x2 − 2y x

Для того чтобы векторное поле F

было потенциальным,

необходимо, чтобы в

каждой точке этого поля выполнялось условие

rotF

= 0.

Следовательно, данное векторное поле F −потенциальное и имеет скалярный

потенциал, то есть функцию U (x, y, z) такую, что выполняется равенство

F(x, y, z) = gradU (x, y, z).

Найдем потенциал по формуле

x

y

z

U (x, y, z) = ∫P(x, y0 , z0 )dx +

∫Q(x, y, z0 )dy + ∫R(x, y, z)dz +C ,

x0

y0

z0

положив x0 = y0 = z0 = 0 , так как никаких особенностей область задания

вектора F

не имеет,

U (x, y, z) = x (2x 0 + 0)dx + y

x2

− 2y dy + z (x)dz +C = x2 y − y2 + xz +C ,

∫

∫(

)

∫

0

0

0

где C - произвольная постоянная.

63

Проверим полученный результат. Так как F = gradU , то

gradU = ∂∂Ux i + ∂∂Uy j + ∂∂Uz k = (2xy + z)i + (x2 − 2y) j + xk = F

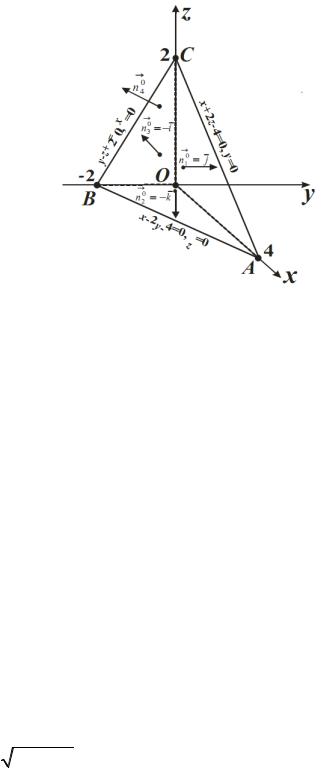
10. Вычислить (непосредственно или по формуле Остроградского – Гаусса) поток векторного поля F =(x + z)i +(2y − x) j + zk через внешнюю поверхность пирамиды, образуемую плоскостью x − 2y + 2z = 4 и координатными плоскостями.

Решение:																				= ∫∫F
а).	Непосредственно: По определению, имеем:																	П							n0dS, где
S −внешняя сторона поверхности пирамиды ABCO.																							S
1.	Грань AOC лежит в плоскости y = 0,												n0 = j ,					dS = dxdz
									4	2−	x					4																			4
											2											x							2			x3					16
П1 = − ∫∫		xdS = − − ∫∫				xdxdz = −∫xdx ∫ dz = −∫x													2 −					dx = − x						−					0	= −		.
																						2										6					3
	∆AOC				∆AOC				0	0						0
2.	Грань AOB лежит в плоскости z = 0,												n0 = −k				,		dS = dxdy
П2 = − ∫∫ 0 dxdy = 0.
	∆AOB												n0 = −i ,
3.	Грань BOC лежит в плоскости x = 0,																		dS = dydz
				2		0			2												z3				2		2			4
П3 = − ∫∫		zdydz = −∫zdz ∫						dy = −∫z(−z + 2)dz = − −																+ z			0	= −			.
																					3									3
	∆BOC			0		z−2			0
4.	Грань ABC			лежит в плоскости x − 2y + 2z − 4 = 0, а нормаль к этой грани
		0		i − 2 j +		2k		i − 2	j + 2k				1			2					2
имеет вид		n	=					=	3	=			3	i	−	3			j +		3		k,,
				1+ 4 + 4
										64

													dxdy,						1 x + y + 2,								z′x = −1 ,
dS =				1+(z′x )2 +(z′y )2											z = −																z′y =1
									dxdy = 3 dxdy,										2											2
dS =							1+ 1	+1
			3		2		4						2														2 ∆∫∫ABC
							∆∫∫ABC
П4 = 1 3							(x+ z)− 2(2y								− x)+ 27 dxdy =											1				(3x− 4y+3z)dxdy =
=	1	∆∫∫ABC				3x − 4y −3					1		x +3y								1	∆∫∫ABC						3	x	− y	+ 6
	2										2										2							2
															+ 6 dxdy =																	dxdy =
=	1 0				2 y+4 3			x − y		+				=	1			0	3	(2y	+	4)	2
	2 −∫2		dy									6 dx			2				4						+(6 − y)(2y + 4) dy =
						∫0 2											−∫2
	1	0	(y2 + 20y +36)dy = 1												y	3											0			52.
=		∫																+10y2 +36y											=
																											−2
	2	−2											2		3															3

Следовательно, П = П1 + П2 + П3 + П4 = 323 .

б). По формуле Остроградского – Гаусса: Имеем

П = ∫∫∫divFdV,

V

divF = ∂∂Px + ∂∂Qy + ∂∂Rz = ∂∂x (x + z)+ ∂∂y (2y − x)+ ∂∂z (z)=1+ 2 +1 = 4, поэтому

									1 Sосн. h , то
П = ∫∫∫divFdV = 4∫∫∫dxdydz = 4 Vпирамиды, но т.к. Vпирамиды =
	V				V		= 4 1	4 2 = 32.	3
окончательно получаем: П = 4 V
						пирамиды	3	3
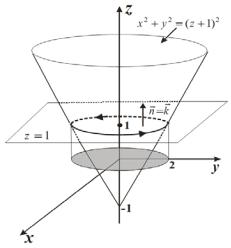
11. Вычислить (непосредственно или по формуле Стокса)										циркуляцию
векторного поля F						= (3y −5x)i + (6x +5y) j + (4z − xy + 4)k				по контуру
	2		2		2
L : x		+ y		= (z +1)		,
z =1.

а). Непосредственно:

65

По определению циркуляция векторного поля F по контуру L равна

∫	Fdl = ∫(3y −5x)dx + (6x +5y)dy + (4z − xy + 4)dz.
L	L
Здесь контуром L	является окружность x2 + y2 = 4, полученная в результате

сечения конуса x2 + y2 = (z +1)2 плоскостью z =1. Параметрические уравнения этой линии имеют вид

x = 2cost,y = 2sint,

z =1.

Отсюда находим dx = −2sintdt,dy = 2costdt,dz = 0. Направление обхода контура выбирается таким образом, чтобы ограниченная им область оставалась слева. Следовательно, обход окружности x2 + y2 = 4 будем

совершать против часовой стрелки, если смотреть с конца оси Oz . Тогда 0 ≤t ≤ 2π . Теперь, переходя к определенному интегралу, найдем искомую циркуляцию

∫Fdl = ∫(3y −5x)dx + (6x +5y)dy + (4z − xy + 4)dz =

L L

= 2∫π ((6sint −10cost)(−2sint)

0

б). По формуле Стокса:

Вычислим ротор векторного поля F = по формуле

		i		j		k				i
		∂		∂		∂				∂
rotF =								=
		∂x		∂y		∂z				∂x
		P		Q		R			3y −5x

+ 2(12cost +10sint)cost)dt =12π .

(3y −5x)i + (6x +5y) j + (4z − xy + 4)k

	j		k			= −xi + yj +3k.
	∂		∂
	∂y		∂z
6x +5y 4z − xy + 4

66

Применим формулу Стокса C = ∫∫rotF ndσ , где в качестве поверхности σ ,
					σ
		2		2		2	, , возьмем часть плоскости z =1,
натянутой на контур	L : x		+ y		= (z +1)
	z =1.

ограниченную окружностью x2 + y2 = 4, то есть круг радиуса R = 2 . Тогда

единичный вектор нормали n = k и скалярное произведение rotF n =3. Следовательно,

						dxdy			2π	2
	∫	Fdl	= ∫∫rotF	ndσ = 3∫∫dσ = 3∫∫			= 3	∫∫	dxdy = 3 ∫dϕ∫rdr =12π .
						| cosγ |
	L		σ	σ	Sσ			x2 +z2 =4	0	0

67

3. Варианты контрольных заданий по дифференциальным уравнениям

Вариант 1

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

впримерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

впримере 10 написать общее решение дифференциального уравнения

со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

впримере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейлора);

впримерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

1.1y′ =5x+y .

1.22x2 y′ = x2 + y2 .

1.3y′+ y = x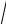y .

x

2

+

y

2

2

+

y

2

1.4

2x +

dx =

x

dy .

2

xy

2

x y

1.5y3 y′′+1 = 0 .

1.6x2 y′′ = y′2 .

1.7y′′(x + 2)5 =1; y(−1)=121 , y′(−1)= −14 .

1.8y′′′+ y′ = 0; y(0)=1, y′(0)= −1, y′′(0)= 0 .

1.9y′′−3y′+ 2y = (x2 + x)e3x .

1.10y′′′+ 4y′′ = x −1+ cos4x .

	′′		2		π2
1.11 y		+π		y = cosπx .

1.12y′ = xy + ey ; y(0)= 0.

1.13Записать уравнение кривой, проходящей через точку A(0; 2), если

известно, что угловой коэффициент касательной в любой ее точке равняется ординате этой точки, увеличенной в 3 раза.

1.14 Найти силу тока в катушке в момент t , если ее сопротивление R , индуктивность L , а электродвижущая сила (эдс) меняется по закону E = E0 sinωt . Начальная сила тока i0 = 0 .

68

Вариант 2

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

впримерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

впримере 10 написать общее решение дифференциального уравнения

со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

впримере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейлора);

впримерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

2.1x dydx + y =1.

2.2y′ = xy + xy .

2.3(sin2 y + xctgy)y′ =1.

2.4e−ydx −(2y + xe−y )dy = 0.

2.5(1+ x2 )y′′− 2xy′ = 0; y(0)= 0; y′(0)= 3.

2.6y′′(x +1)− 2y′ = 0 .

2.7y′′ = 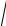1+ y′2 .

2.8y′′′−5y′′+8y′− 4y = 0; y(0)= 0, y′(0)= −1, y′′(0)= −3.

2.9y′′− 2y′+ y = 6xex .

2.10y′′−3y′ = x + cosx.

2.11 y′′+3y′ =	9e3x
		.
	1+ e3x

2.12y′′−(1+ x2 )y = 0; y(0)= −2, y′(0)= 2 .

2.13Записать уравнение кривой, проходящей через точку A(2; 5), если

известно, что угловой коэффициент касательной в любой ее точке в 8 раз больше углового коэффициента прямой, соединяющей ту же точку с началом координат.

2.14 За сколько времени тело, нагретое до 1000 , в комнате с температурой Т0 = 200 охладится до 250 , если до 600 оно охладится за 10 мин.?

69

Вариант 3

В примерах с 1 по 14 решить задачи в соответствии с условиями варианта задания:

впримерах 1- 9, 11 найти общее решение (общий интеграл) или частное решение дифференциального уравнения;

впримере 10 написать общее решение дифференциального уравнения

со специальной правой частью, не находя числовых значений неопределенных коэффициентов частного решения;

впримере 12 решить дифференциальное уравнение с помощью формулы Тейлора (найти первые три ненулевых члена разложения по формуле Тейлора);

впримерах 13-14 решить геометрическую и физическую задачу, путем составления дифференциального уравнения.

3.1y′ = cos(y − x).

3.2y′ = xx +− yy .

3.3xy′+ y = ex , y(1)=1.

3.4(3x2 − 2 − 2x − y)dx +(2y − x +3y2 )dy = 0 .

3.5yIV = x .

3.6x3 y′′+ x2 y′ =1.

3.7(y′)2 = y′′(y −1).

3.8y′′′−5y′′ = 0; y(0)=5, y′(0)= 28, y′′(0)=125 .

3.9y′′+ y = sin x .

3.10y′′+3y′− 4y = e−4x + xe−x .

3.11y′′+ 4y =8ctg2x .

3.12 y′ = x2 y2 +1; y(0)=1.

3.13 Записать уравнение кривой, проходящей через точку A(0; 4), если

известно, что длина отрезка, отсекаемого на оси ординат нормалью, проведенной в любой точке кривой, равна расстоянию от этой точки до начала координат.

3.14 Катер движется со скоростью 18 км/ч. Через 5 мин после выключения мотора его скорость уменьшилась до 6 км/ч. Найти расстояние, пройденное катером по инерции за 15 мин, если сопротивление воды пропорционально скорости движения катера.

70