6.2. Планирование сети дорог

Рассмотренная постановка задачи о прокладке коммуникаций не учитывает возможность их разветвления. Зачастую реальность не накладывает этих ограничений, например, при строительстве дорог, которые могут менять направление, иметь повороты, развилки и перекрестки любого вида. Данная задача известна как «задача Штейнера на графах».

Сразу же зададимся вопросом: а может ли расположение развилок вне связываемых объектов уменьшить длину кратчайшей системы дорог? Пример, иллюстрирующий положительный ответ на этот вопрос, приведен на рис. 6.2.

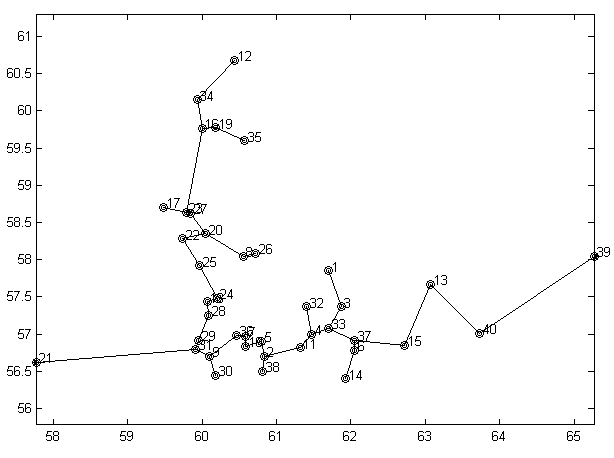
Рис. 6.1. Остовное дерево для Свердловской области

10 9,928... 9,196...

Рис. 6.2. Изменение длины связей в задаче Штейнера

НЕОБХОДИМЫЕ УТОЧНЕНИЯ

Вообще говоря, известны два типа такого рода задач.

• Евклидова задача Штейнера состоит в соединении множества точек на плоскости так, чтобы сумма длин отрезков была минимальна.

• Линейная задача Штейнера вместо евклидова расстояния между точками оперирует линейным расстоянием 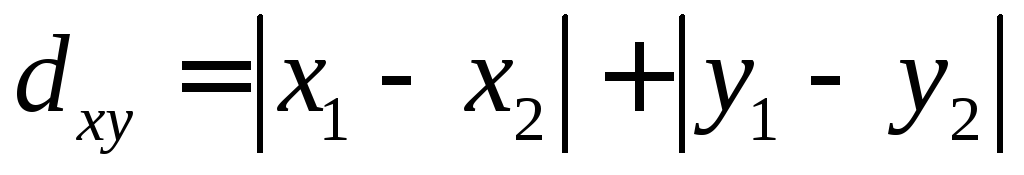. При этих условиях, если через каждую точку из множества Р провести вертикальные и горизонтальные линии, то решение данной задачи можно получить, рассматривая в качестве возможных точек Штейнера точки пересечения полученной сетки линий.

Линейные задачи Штейнера в основном применяются при монтаже печатных схем электронных устройств, а в логистике могут применяться, например, в задачах построения маршрута в условиях города с планировкой клеточного типа.

Евклидовы задачи Штейнера применяются достаточно широко.

ОПИСАНИЕ АЛГОРИТМА

Основная идея

Такой алгоритм в общем случае не существует. Евклидова задача Штейнера является нерешенной с вычислительной точки зрения, поскольку существующие точные алгоритмы находят решение за разумное время только при очень небольшом количестве вершин (порядка 10).

ПРИМЕЧАНИЕ

Частный случай: три города

Если целью является система дорог, связывающая три города, то мы в чистом виде имеем старинную задачу, которую независимо поставили Торичелли и Ферма: в треугольнике ABC найти точку P, такую что сумма расстояний от P до вершин A, В и C минимальна.

Частный случай: четыре города

Если целью является система дорог, связывающая четыре города, то для ее решения используем результат, полученный при рассмотрении задачи Торричелли-Ферма. Вводимые при прокладке пути минимальной длины точки (развилки) в литературе называются точками Штейнера.

Ключевыми свойствами точек Штейнера являются следующие свойства:

• Точка Штейнера имеет степень d=3.

• Для любой вершины p_t из множества связываемых сетью объектов выполняется условие: степень d (p_t)< 3. Если d (p_t) = 3, то угол между любыми двумя ребрами, инцидентными p_t, должен быть равен 120°. Если d (p_t) = 2, то угол между двумя ребрами, инцидентными p _и должен быть больше или равен 120°.

• Если в исследуемой сети N объектов, то количество k точек Штейнера будет в пределах 0<k<N-2.

Отсюда следует решение для рассматриваемого случая. Введем две точки Штейнера, каждая из них будет иметь степень d = 3, а инцидентные ей ребра располагаться под углом 120° друг к другу. Расположение точек зависит от свойств фигуры, образуемой четырьмя объектами.

Анализ сложности

Возрастание сложности связано с потерей дискретности, поскольку расположение перекрестков уже не совпадает с самими объектами, и строго говоря, на площади в 1 кв. м существует бесконечное количество возможных мест расположения развилок. Очевидно, что в общем случае теория графов уже не может дать достоверного результата при решении этой задачи. Мало того, в настоящее время неизвестны точные и эффективные алгоритмы, решающие эту задачу в том случае, если города заданы произвольной сетью. Точное и эффективное решение существует, если рассматриваются относительно простые сети.

В качестве примера приведем решение задачи Штейнера для городов Свердловской области, описанных выше (рис. 6.3). Суммарная длина связей в приведенном решении составила 1930 км при длине остовного дерева 1982 км.

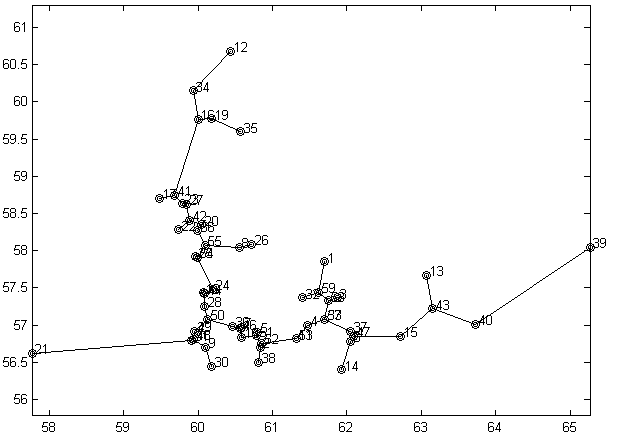
Рис. 6.3. Решение задачи Штейнера для остовного дерева,

изображенного на рис. 6.1