6. Задачи прокладки коммуникаций

Основной тип задач – проблемы прокладки коммуникаций (трубопроводов, телефонных линий) и строительства системы дорог, причем иногда последнюю задачу усложняют различные естественные и искусственные препятствия. Типичные проблемы и соответствующие алгоритмы их решения изложены в рамках задач: о телефонных линиях, о строительстве дорог, строительной трассировки.

6.1. Прокладка коммуникаций

В задачи отдела логистики входят функции по оптимальному размещению различного рода коммуникаций. В разных случаях дополнительные условия размещения могут отличаться, но в большинстве ситуаций критерием оптимальности является суммарная длина размещаемых коммуникаций.

Задачи такого рода имеют общую смысловую модель: дана плоскость и на ней N объектов. Заданы расстояния между объектами. Соединить объекты отрезками между собой так, чтобы суммарная длина отрезков была минимальной.

НЕОБХОДИМЫЕ УТОЧНЕНИЯ

1. Допустим, что объекты относительно малы по сравнению с расстояниями между ними. Поэтому величиной объектов можно пренебречь и изображать их в виде точек.

2. Расстояния между объектами могут быть заданы двумя способами: в натуральном виде (как число метров, километров и т.д.) или опосредованно через задание положения объекта относительно какой-либо точки отсчета. Во втором случае вводится подходящая система декартовых координат и положение i-го объекта, где , задается парой координат 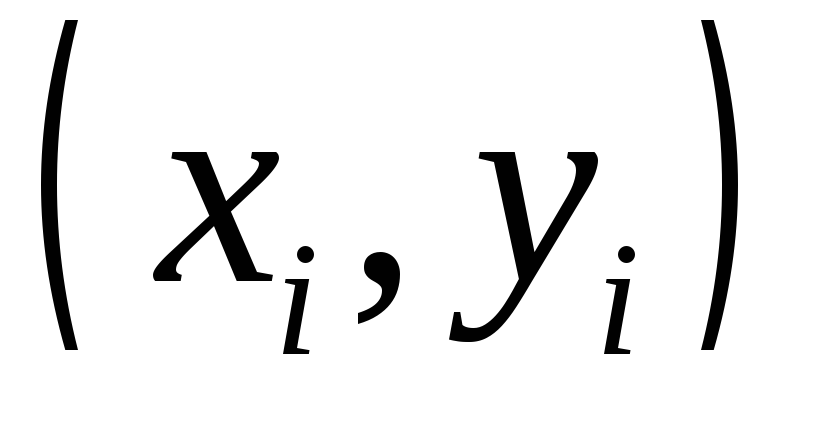. Условие, что страна плоская, означает, чторасстояние от i-го объекта до j-го задается формулой

.

1. Подразумевается транзитивность связи, то есть, если i-й объект связан с j-м объектом, а j-й с k-м, то i-й связан с k-м.

2. Подразумевается или указано явно, что коммуникации могут разветвляться только на территории связываемых объектов.

3. И, наконец, на основе элементарной логики можно утверждать, что в оптимальном решении не будет циклов. Если бы в оптимальном решении был цикл, скажем, (i, j, k, l, i), то можно было бы убрать одно звено цикла, скажем, (j, k), причем связь между j и k сохранилась бы по другой стороне цикла, по пути (j, i, l, k). Но, убирая одно звено, мы бы уменьшили минимальный цикл, что невозможно.

ПОСТАНОВКА ЗАДАЧИ

После такой конкретизации можно вводить графовую модель, в рамках которой объекты становятся вершинами, а возможные связи между ними – ребрами. Расстояния между объектами заданы в виде таблицы, которая в точности совпадает с матрицей смежности, задающей произвольный граф.

В терминах теории графов такая задача независимо была поставлена и решена двумя математиками: Примом (Prim) и Краскалом (Kruskal).

Постановка Прима.

Дан полный граф с N вершинами, длины ребер определяются по формуле ,где , – координаты вершин. Найти остовное дерево минимальной длины.

Постановка Краскала.

Дан граф с N вершинами, длины ребер заданы матрицей , где . Найти остовное дерево минимальной длины.

Постановка Краскала отличается тем, что расстояния между вершинами заданы явно, т.е. являются любыми произвольными положительными числами , . В этом случае может не работать так называемое правило треугольника, согласно которому . На плоскости, если объекты соединяются прямыми, так оно и есть (кратчайшее расстояние между объектами равно длине соединяющего их отрезка, и путь, пролегающий через третий объект в лучшем случае будет равен длине этого отрезка, если третий объект находится на самом отрезке). Однако в реальности коммуникации прокладываются с учетом местности, и вполне может оказаться, что данное правило не работает потому, что за расстояние берется не абсолютная величина, характеризующая географическую удаленность, а длина связывающих коммуникаций. Кроме того, в постановке Краскала для некоторых пар индексов возможна ситуация, когда , что означает отсутствие ребра, т.е. рассматривается любой граф, а не только полный. Это как раз интерпретация задачи, когда коммуникации могут быть проложены не между любой парой объектов или стоимость прокладки между разными парами объектов неодинакова. В реальности именно так чаще всего и бывает, из-за уже имеющихся каналов связи (по которым класть дополнительные коммуникации чаще всего дешевле) и ландшафтных особенностей местности (водоемы, качество грунта) или административных запретов.

Задачи данного класса решаются одним алгоритмом, причем весьма примитивного характера. В литературе его часто называют «жадным». Его суть в последовательном выборе самых выгодных (в данном случае коротких) ребер. В обычной жизни и в большинстве графовых задач за такую политику приходится жестоко расплачиваться на последних шагах. Несмотря на то, что задача Прима-Краскала, не является простой, жадный алгоритм дает точное оптимальное решение.

ОПИСАНИЕ АЛГОРИТМА (КРАСКАЛА)

Необходимая теоретическая информация

Дерево на N вершинах имеет N-1 ребер. Т.к. решением является остов графа, значит, в него тоже войдут N-1 ребер.

Основная идея

Каждое ребро надо выбирать «жадно» так, чтобы не возникали циклы. Выбранные таким образом ребра образуют искомое остовное дерево.

Возможные сложности

Нужно обязательно следить, чтобы новое ребро не образовывало цикла со старыми. Для ручной реализации алгоритма при небольшом количестве объектов можно обойтись визуальным наблюдением. Однако, если таких объектов много, например, более 20, или если решение отыскивается автоматизированным образом (при помощи соответствующей программы), нужен строгий алгоритм, обеспечивающий отсутствие циклов из выбираемых ребер графа.

Способы преодоления

До построения дерева окрасим каждую вершину в отличный от других цветi. Получится N цветов. При выборе очередного ребра, скажем , будем руководствоватьсяправилом: i и j должны иметь разные цвета. Когда же выбор ребра осуществлен, новая вершина красится в цвет вершин, входящих в построенное остовное дерево. Таким образом, выбор вершин разного цвета обеспечивает отсутствие циклов. После выбора N-1 ребер все вершины получают один цвет.

В качестве примера приведем минимальное остовное дерево для 40 крупнейших городов Свердловской области (рис. 6.1).