7. Задачи поиска оптимальных путей

Основная задача – проблема поиска кратчайших путей между объектами, если определенная сеть дорог уже проложена. Например, если после каждой доставки (например, с базы до пункта А) необходимо возвращение автотранспорта на базу для загрузки новой партии товара (такая ситуация часто возникает, если потребность в продукции больше объема единовременно перевозимых товаров), то задача специалистов отдела логистики – рассчитать кратчайшие пути между данным объектом (базой) и всеми прочими объектами (потребителями). Также к этому относится задача определения кратчайших путей между всеми парами объектов в рамках заданной сети дорог, подобная формулировка принимается, если включаются связи между потребителями в сети, например в случае оптовой и мелкооптовой торговли.

В рассмотренных ранее задачах речь шла о прокладке коммуникаций или сети дорог, что называется «в чистом поле». В реальной жизни зачастую сеть дорог уже существует, причем сеть, разветвленная и явно неоптимальная и, как правило, избыточная, т.е. построенная не по Штейнеру и наверняка с множественными путями между некоторыми парами городов, что обусловлено постепенной и, как правило, длительной застройкой, во время которой неоднократно менялось значение и размер связываемых городов, требования к самим дорогам, власть и прочие условия.

Если сеть дорог уже существует, то возникает прикладная и очень актуальная задача поиска кратчайшего расстояния между некоторыми объектами в этой сети.

НЕОБХОДИМЫЕ УТОЧНЕНИЯ

Для более точной постановки вопроса отождествим развилки и города: они будут вершинами сети, а дороги будут ребрами. Однако для решения прикладных логистических задач, в частности ряда задач о минимальной стоимости доставки грузов из пункта А в пункт В, сеть не всегда будет неориентированной. В реальности часто бывает, что возможность проезда из города А в город Б вовсе не означает наличие прямой дороги из Б в А, или стоимость проезда на поезде из Москвы в Киев не имеет никакого отношения к стоимости проезда из Киева в Москву. В этом случае воспользуемся ориентированными графами, заменив ребра парой разнонаправленных дуг, имеющих различные веса (равные бесконечности, если прямое сообщение между связываемыми объектами отсутствует).

Существуют как общие алгоритмы решения подобных задач, так и частные алгоритмы для случаев, когда все веса ребер неотрицательны. Если вес ребра графа соответствует расстоянию между объектами, времени в пути или стоимости доставки, то не возникает необходимости в рассмотрении случая с отрицательными весами. Именно таких задач больше всего встречается в логистике, так что рассмотрение этих специальных (и более простых) алгоритмов вполне оправдано.

Если же некоторые ребра имеют отрицательный вес, то единственное ограничение состоит в том, чтобы в G не было циклов с суммарным отрицательным весом. Если такой цикл Ф все же существует и v_t — некоторая его вершина, то, двигаясь от s к v_t, обходя затем Ф достаточно большое число раз и попадая, наконец, в t, мы получим путь со сколь угодно малым () весом. Таким образом, в этом случае кратчайшего пути не существует.

Если, с другой стороны, такие циклы существуют, но исключаются из рассмотрения, то нахождение кратчайшего пути (простой цепи) между sиt эквивалентно нахождению в этом графе кратчайшего гамильтонова пути с концевыми вершинами s и t. Задача нахождения кратчайшего гамильтонова пути намного сложнее, чем задача о кратчайшем пути - поэтому в рамках данного пособия рассматривать ее не будем и предположим, что все циклы в G имеют неотрицательный суммарный вес. Отсюда также вытекает, что неориентированные дуги (ребра) графа G не могут иметь отрицательные веса.

ПОСТАНОВКА ЗАДАЧИ

В ориентированной, неориентированной или смешанной (т. е. где часть дорог имеет одностороннее движение) сети найти кратчайший путь из заданной вершины во все остальные.

Возможные постановки задачи

Пусть дан граф , дугам которого приписаны веса (стоимости), задаваемые матрицей . Элементы матрицывесов С могут быть в общем случае положительными, отрицательными или нулями.

1. Найти кратчайший путь от заданной начальной вершины 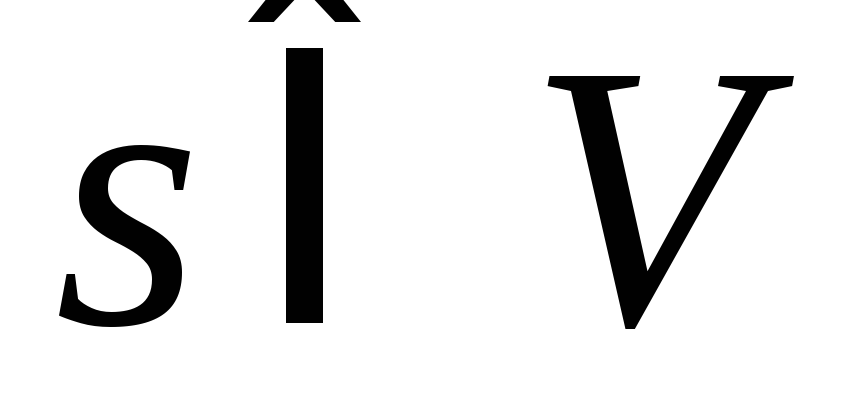до заданной конечной вершины .

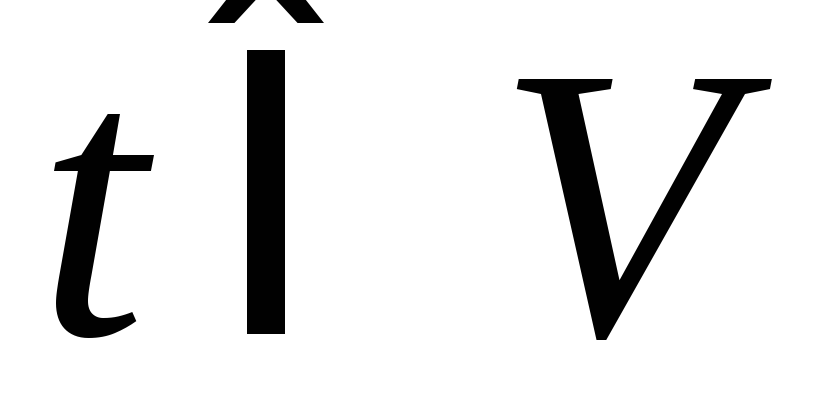2. Найти кратчайшие пути от заданной начальной вершины 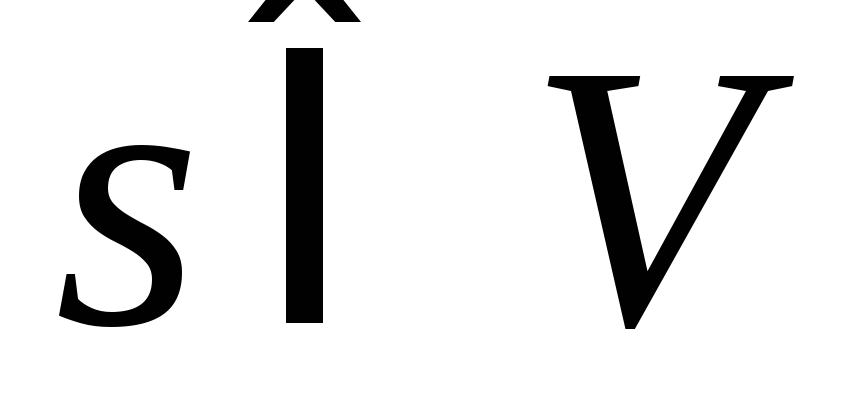до всех других вершин .

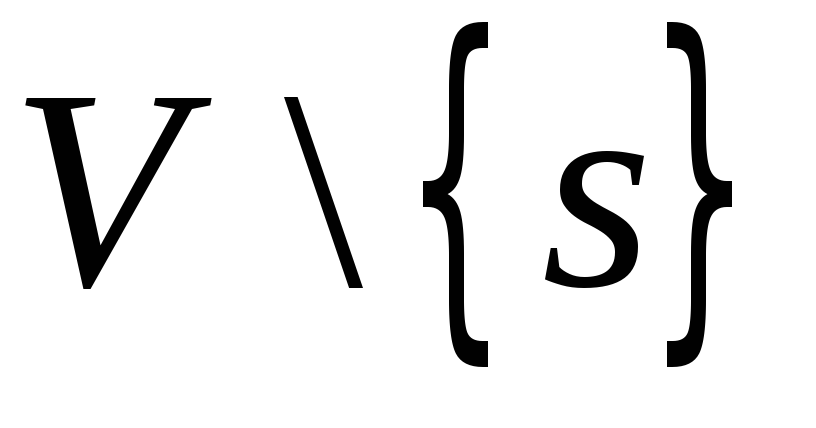3. Найти кратчайшие пути между всеми парами вершин.

Во всех трех случаях поиск кратчайшего пути между s и t имеет смысл, если такой путь, вообще говоря, существует, т. е. при условии. Здесь – множество достижимости для вершины s, то есть множество всех вершин, для которых существует путь из заданной вершины. В случае неориентированного связного графа такой путь существует между любой парой вершин (по определению связности).

На самом деле, почти все методы, позволяющие решить задачу I о кратчайшем (s-t)-пути, дают также (в процессе решения) и все кратчайшие пути от начальной вершины до всех, которые используются в процессе решения задачи. Таким образом, они позволяют решить задачу II с небольшими дополнительными вычислительными затратами. С другой стороны, задача III может быть решена либо N-кратным применением алгоритма задачи I, причем на каждом шаге в качестве начальной вершины s берутся различные вершины, либо однократным применением специального алгоритма.

Как и для большинства задач, для решения задачи о кратчайших путях можно предложить много процедур решения. Например, физическое моделирование такого рода: на плоской доске рисуется карта местности, в города и развилки вбиваются гвозди, на каждый гвоздь надевается кольцо, дороги укладываются веревками, которые привязываются к соответствующим кольцам. Чтобы найти кратчайшее расстояние между кольцом i и кольцом k, нужно взять i в одну руку, взять k в другую и растянуть. Те веревки, которые натянутся и не дадут разводить руки шире, и образуют кратчайший путь между i и k. Однако математическая процедура, которая промоделирует эту физическую, выглядит очень сложно.

Известны алгоритмы попроще, один из которых будет описан далее. Это алгоритм, предложенный Дейкстрой еще в 1959 г. для систем с неотрицательными значениями весов. Алгоритм Дейкстры в чистом виде решает задачу II (а значит автоматически и задачу I за то же время, и задачу III в случае N-кратного применения).

Описание алгоритма.

Каждой вершине из V сопоставим метку – минимальное известное расстояние от этой вершины до a. Алгоритм работает пошагово, то есть на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.

Инициализация.

Метка самой вершины a полагается равной нулю, метки остальных вершин – бесконечности. Это отражает то, что расстояния от a до других вершин пока неизвестны. Все вершины графа помечаются как непосещённые.

Шаг алгоритма.

Если все вершины посещены, алгоритм завершается. В противном случае, из ещё не посещённых вершин выбирается вершина u, имеющая минимальную метку. Мы рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом. Вершины, в которые ведут рёбра из u, назовем соседями этой вершины. Для каждого соседа вершины u, кроме отмеченных как посещённые, рассмотрим новую длину пути, равную сумме значений текущей метки u и длины ребра, соединяющего u с этим соседом. Если полученное значение длины меньше значения метки соседа, заменим значение метки полученным значением длины. Рассмотрев всех соседей, пометим вершину u как посещенную и повторим шаг алгоритма.

Пример.

Рассмотрим выполнение алгоритма на примере графа, показанного на рис. 7.1. Пусть требуется найти кратчайшие расстояния от первой вершины до всех остальных.

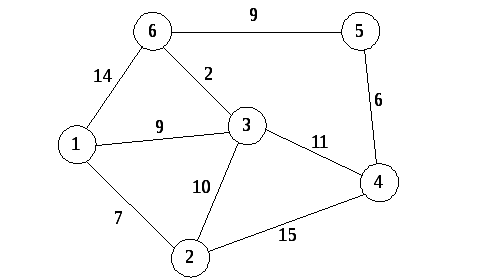
Рис. 7.1. Пример графа

Кружками обозначены вершины, линиями – пути между ними (ребра графа). В кружках обозначены номера вершин, около каждого ребра обозначен их «вес» – длина пути. Рядом с каждой вершиной обозначена метка – длина кратчайшего пути в эту вершину из вершины 1 (Рис.7.2).

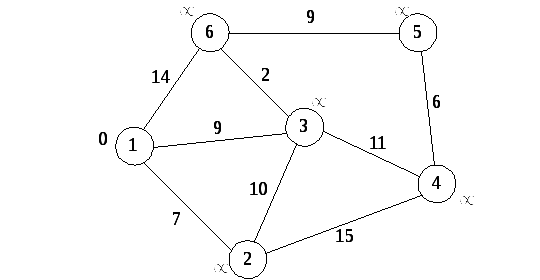
Рис. 7.2. Начальное состояние графа

Первый шаг. Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет начальная вершина 1. Её соседями являются вершины 2, 3 и 6. Первый по очереди сосед вершины 1 – вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна сумме кратчайшего расстояния до вершины 1, значению её метки, и длины ребра, идущего из 1-ой во 2-ю, то есть 0+7=7. Это меньше текущей метки вершины 2, бесконечности, поэтому новая метка 2-й вершины равна 7. Аналогичную операцию проделываем с двумя другими соседями 1-й вершины – 3-й и 6-й (Рис.7.3).

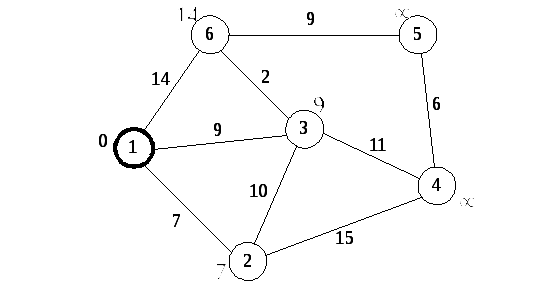
Рис. 7.3. Первый шаг. Пометка смежных вершин

Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Э. Дейкстра). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена (Рис. 7.4).

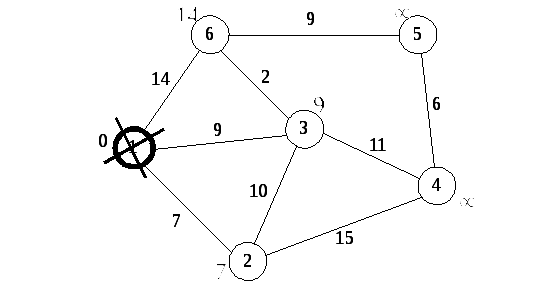
Рис. 7.4. Первый шаг. Вычеркивание начальной вершины

Второй шаг. Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7. Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю вершину. Соседями вершины 2 являются вершины 1, 3 и 4. Первый (по порядку) сосед вершины 2 – вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем. Следующий сосед вершины 2 – вершина 3, так как имеет минимальную метку из вершин, отмеченных как не посещённые. Если идти в неё через 2, то длина такого пути будет равна 17 (7+10=17). Но текущая метка третьей вершины равна 9, а это меньше 17, поэтому метка не меняется. Ещё один сосед вершины 2 – вершина 4. Если идти в неё через 2-ю, то длина такого пути будет равна сумме кратчайшего расстояния до 2-й вершины и расстояния между вершинами 2 и 4, то есть 22 (7+15=22). Поскольку 22<, устанавливаем метку вершины 4 равной 22 (Рис. 7.5).

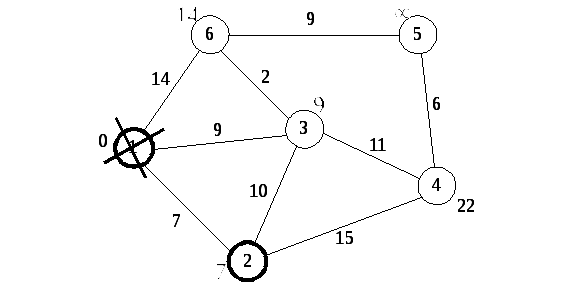
Рис. 7.5. Второй шаг. Пометка смежных вершин

Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещенную (Рис. 7.6).

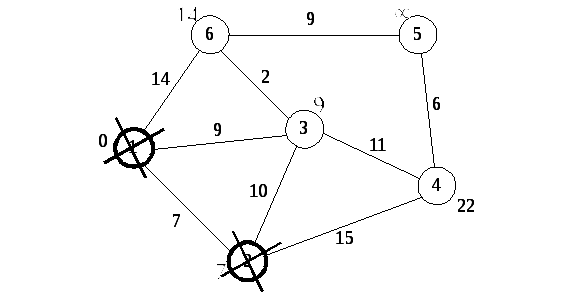
Рис. 7.6. Второй шаг. Вычеркивание второй вершины

Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты, изображенные на рис. 7.7.

Рис. 7.7. Третий шаг

Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин. Это будут вершины 6, 4 и 5, соответственно порядку (Рис. 7.8).

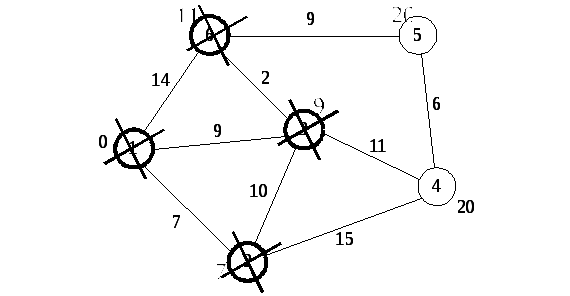
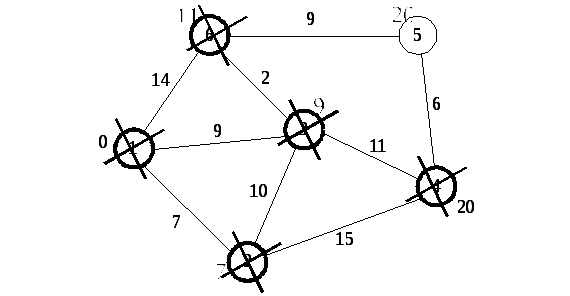
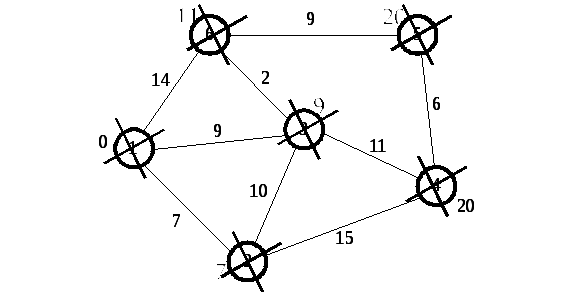
Рис. 7.8. Последующие шаги

Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда нельзя больше обработать ни одной вершины. В данном примере все вершины зачеркнуты, однако ошибочно полагать, что так будет в любом примере - некоторые вершины могут остаться не зачеркнутыми, если до них нельзя добраться. Результат работы алгоритма виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й – 9, до 4-й – 20, до 5-й – 20, до 6-й – 11.