2.6. Метод бинарных (парных) соотношений

Если совместная оценка всех параметров вызывает затруднения, их можно сравнивать попарно, т.е. методом попарных соотношений. При использовании этого метода каждый i-ый эксперт назначает парные соотношения

и для i-го эксперта составляется расчетная таблица 2.3, причем

,

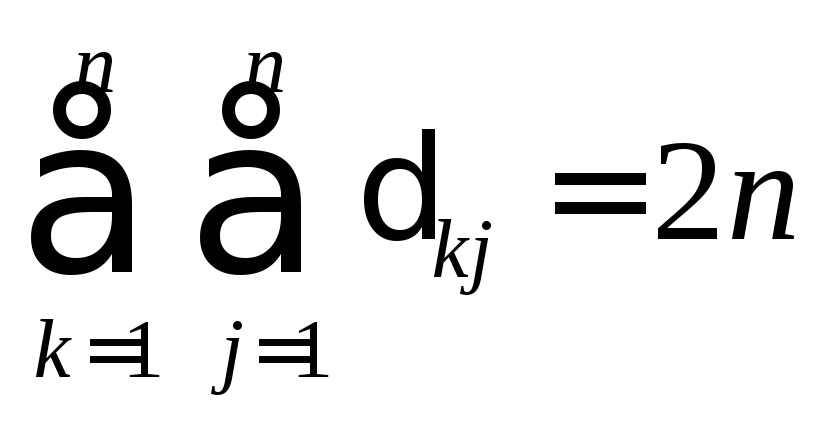где – количество параметров.

Таблица2.3

Сравниваемые параметры		…		…
		…		…
…	…	…	…	…	…
		…		…
…	…	…	…	…	…
		…		…

Приведенные методы определения коэффициентов веса дают возможность получить достаточно достоверные исходные данные, позволяющие оценить важность каждого оптимизируемого параметра.

3. Транспортная задача

Рассмотрим задачу, когда помимо N потребителей продукции существует несколько ее производителей, с неодинаковым в общем случае количеством выпускаемой продукции. Естественно, что стоимость доставки продукции неодинакова для различных пар «производитель-потребитель». Если при этом предположить, что эти производители входят в одну компанию (холдинг), то сразу встает вопрос о минимизации суммарных расходов на транспортировку при условии обеспечения всех потребителей нужным количеством товара.

Будем считать, что компания производителей выпускает ровно столько продукции, сколько требуется всем N потребителям. Такая задача обычно называется транспортной.

ПОСТАНОВКА ЗАДАЧИ

Пусть поставщиков располагают,единицами некоторой продукции, которая должна быть доставленапотребителям в количествах,. Известна стоимостьперевозки единицы продукции от-го поставщика к-му потребителю, задаваемая неотрицательной матрицейразмерности. Требуется определить такие объемы перевозокот каждого поставщика к каждому потребителю, чтобы суммарные затраты на перевозки были наименьшими и потребности всех потребителей были бы удовлетворены.

Составим математическую модель замкнутой транспортной задачи. Поскольку от -го поставщика к-му потребителю планируется перевезтиединиц продукции, стоимость такой перевозки составит. Стоимость всех перевозок выражается двойной суммой.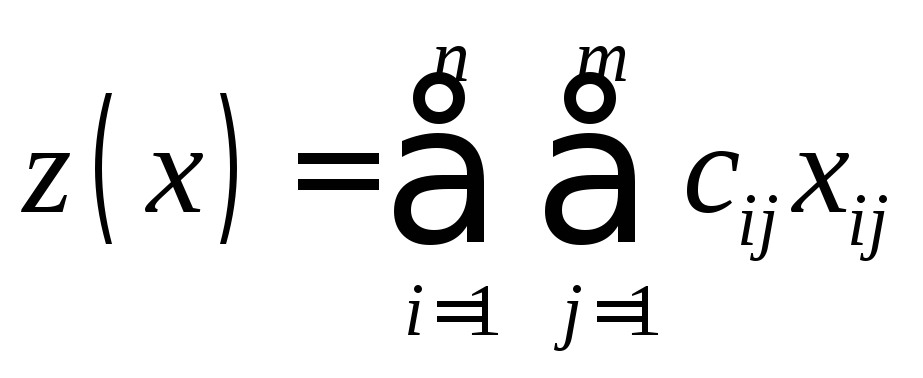

Таким образом, математическая модель замкнутой транспортной задачи имеет следующий вид:

, , ,.

НЕОБХОДИМЫЕ УТОЧНЕНИЯ

Это весьма реалистическая постановка задачи. Единственная натяжка – линейная зависимость цены перевозки от ее величины. Ну, скажем, если производителями являются пекарни, а потребителями – булочные, то нелепо утверждать, что перевозка одной булки в два раза дешевле, чем перевозка двух булок. Однако если считать товар не в булках, а в грузовиках, то линейность становится вполне реалистическим предположением.

Вообще говоря, это типичная задача линейного программирования, когда дан функционал который необходимо минимизировать или максимизировать при заданных линейных ограничениях. В терминах линейного программирования транспортная задача ставится так: найти такой план перевозок, чтобы минимизировать общую стоимость перевозок при наложенных ограничениях полного использования производства и полного удовлетворения спроса.

Эта задача может быть решена стандартными методами, например симплекс-методом, но в результате вполне могут получиться не целые значения . Однако, очевидно, что применение в логистических задачах о доставке таких методов не может быть оправдано, хотя бы потому, что везти полгрузовика продукции вовсе не в два раза дешевле, чем полный грузовик. Таким образом, оптимальное математическое решение задачи не будет соответствовать оптимальной практической реализации. Таким образом, необходимо ограничение на целочисленность результата.

Для этого применим специальный алгоритм решения транспортной задачи, в котором не будет делений, так что, если входные данные a, b, c – целочисленные, то и ответ x будет целочисленным.

ОПИСАНИЕ АЛГОРИТМА

Основная идея

Выбрать некоторую начальную перевозку, соответствующую максимальному ациклическому набору загруженных клеток, посчитать значение функционала. Затем среди оставшихся незагруженных клеток выбрать еще одну, получив цикл, после чего удалить из цикла одну из ранее выбранных перевозок, стремясь таким образом уменьшить значение функционала.

Возможные сложности

1. Выбор начальной перевозки.

2. Выбор новой перевозки для получения цикла.

3. Определение того, какую из имеющихся перевозок убирать для получения ациклического набора.

4. Выявление момента, когда пора прекращать процесс уменьшения функционала.

Способы преодоления

1. Выбор начальной перевозки.

Для инициализации проставляем перевозки жадным алгоритмом по строкам. Принцип следующий: ищем j-го потребителя, к которому i-му поставщику дешевле всего везти продукцию. Полностью удовлетворяем его потребность (записываем в нижней левой части клетки . Далее ищем следующего и т.д. до тех пор, пока полностью потребность удовлетворить уже не удастся, потому как закончится ресурс i-го поставщика. Тогда отдаем этому потребителю все, что есть. Остатки его потребностей удовлетворяем за счет другого поставщика с минимальной стоимостью доставки по заданному столбцу. И так далее, пока не удовлетворим всех потребителей.

В ходе инициализации построен набор из загруженных клеток (включая фиктивные, загруженные нулем), причем этот набор – ациклический.

2. Выбор новой перевозки с целью получения циклического набора.

Для осуществления выбора служат маркеры, которые приписываются каждой строчке (, …,) и каждому столбцу (, …,). Они считаются следующим образом: произвольно назначается маркер какой-либо строки, обычно той, в которой наибольшее число занятых клеток, например, . Найдем в этой строке все загруженные клетки и подпишем под столбцами для каждой из них маркеры, такие, что для загруженной клетки выполняется условие . Теперь, зная , найдем в помеченных столбцах загруженные клетку , для которых стоимость перевозки составляети посчитаем. Далее, через загруженные клетки вычисляем маркеры столбцов , и так до тех пор, пока не пометим все строки и столбцы. Использование данного алгоритма всегда приводит к однозначному нахождению всех значенийи, что вполне очевидно вытекает из ацикличности имеющегося набора.

Теперь будем выбирать клетку , для которой . Это будет незагруженная клетка, потому что для всех загруженных, по построению,. Теперь, вместе с остальными загруженными клетками, весь набор образует единственный цикл. Величинаназывается потенциалом клетки. Опыт расчетов показывает, что итераций часто бывает меньше, если выбирать новую клетку не просто, чтобыбыло положительным, а так, чтобыбыл максимальным.

3. Удаление перевозки для возврата к ациклическому набору.

По построенному циклу перемещаем максимально возможное количество груза. При этом клетка, бывшая свободной, занимается, а одна из занятых клеток освобождается. В некоторых случаях, в частности, если матрица стоимостей является вырожденной, при перемещении грузов освобождается несколько клеток. В такой ситуации при пересчете маркеров при повторе второго шага придется задаваться несколькими маркерами вместо одного.

4. Критерий остановки алгоритма.

Итерации повторяются до тех пор, пока может быть найдена клетка с положительным потенциалом

.

Если все потенциалы незагруженных клеток неположительны, то получена оптимальная система перевозок.

ПРИМЕР ЗАДАЧИ

Три хлебобулочных комбината, принадлежащие одному владельцу, снабжают шесть небольших городов своей продукцией. Потребности городов: 10, 8, 7, 10, 15 и 5 автомашин в неделю, а мощности комбинатов – 10, 15 и 30 машин соответственно. Стоимость проезда одной а/м от i-го комбината к j-му городу задана матрицей С. Найти оптимальное количество поставляемой из комбинатов в города продукции так, чтобы стоимость доставки была минимальной.

Таблица 3.1. Матрица стоимости проезда

Комбинат	Город
	1	2	3	4	5	6
1	3	1	6	5	3	4
2	4	7	2	4	6	5
3	2	5	8	3	6	7

РЕШЕНИЕ ПРИМЕРА

1 итерация. Составим начальный план методом наименьшей стоимости («жадным» алгоритмом), избегая получения вырожденного плана. Составим первую расчетную таблицу (табл. 3.2).

Таблица 3.2.

Поставщики	Потребители
	3 0	1 8	6 0	5 0	3 2	4 0
	4 0	7 0	2 7	4 0	6 3	5 5
	2 10	5 0	8 0	3 10	6 10	7 0

Стоимость перевозок при исполнении этого плана составляет

.

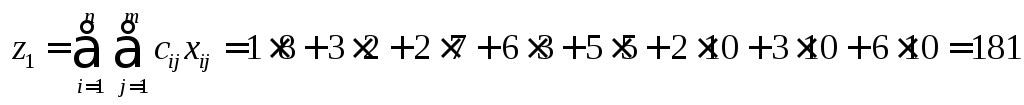Принимаем . В первой строке находим занятые клетки(1,2) и (1,5). Находим маркеры второго и пятого столбцов:

, .

В пятом столбце находим занятые клетки (2,5) и (3,5), а по ним маркеры второй и третьей строк

, .

Во второй строке столбцу находим занятые клетку (2,3) и (2,6), а по ним маркеры третьего и шестого столбцов

, .

В третьей строке находим занятые клетки (3,1) и (3,4), а по ним маркеры первого, и четвертого столбцов

, .

Вносим полученные значения маркеров в расчетную таблицу (табл. 3.3).

Таблица 3.3

Поставщики	Потребители
	3 0	1 8	6 0	5 0	3 2	4 0	1
	4 0	7 0	2 7	4 0	6 3	5 5	4
	2 10	5 0	8 0	3 10	6 10	7 0	4
	-2	0	-2	-1	2	1

Для незанятых клеток вычисляем потенциалы:

,

,

,

,

,

,

,

,

,

.

Поскольку потенциалы всех свободных клеток отрицательны, построенный план перевозок является оптимальным.

Очевидно, метод наименьшей стоимости даёт оптимальный либо близкий к оптимальному начальный план.