8. Задачи размещения

К этому классу относят вопросы об оптимальном размещении различных пунктов обслуживания, как регулярного плана (школы, кинотеатры, парки), так и экстренного характера (больницы, пункты милиции, пожарные депо). Типичные проблемы и соответствующие алгоритмы изложены в рамках задачи о размещении регулярных пунктов обслуживания (минисуммная постановка, алгоритм поиска медианы графа) и задачи о размещении экстренных пунктов обслуживания (минимаксная постановка, алгоритм поиска центра графа).

8.1. Размещение регулярных пунктов обслуживания

Задача о размещении пунктов массового обслуживания для некоторого множества объектов возникает в логистике достаточно часто. Это может быть поиск оптимального места для склада, с которого осуществляется доставка продукции потребителям, или размещение школ, детских садов или кинотеатров, поликлиник, пожарных депо и станций скорой помощи.

Однако, несмотря на схожесть подобных задач, критерии оптимальности чаще всего бывают двух типов. В соответствии с ними разделяют и постановки задачи на размещение пунктов обслуживания.

Минисуммная задача размещения. Дана сеть с обслуживаемыми объектами. Разместить пункт регулярного обслуживания так, чтобы сумма кратчайших расстояний от этого пункта до вершин графа была минимально возможной.

Минимаксная задача размещения. Дана сеть с обслуживаемыми объектами. Разместить пункт экстренного обслуживания так, чтобы расстояние до самого удаленного объекта было минимально возможным.

Рассмотрим минисуммную постановку задачи. Подобная формулировка подходит для размещения автобазы, обслуживающей ряд объектов, центрального склада, с которого осуществляется доставка продукции, школы, коммутатора в телефонной сети и т.д. Однако в реальности вряд ли все обслуживаемые объекты имеют одинаковый приоритет. Например, в случае с размещением склада, очевидно, что объекты с наибольшей потребностью в продукции должны размещаться ближе к складу, поскольку ездить туда придется чаще, а в целом речь идет о минимизации транспортных расходов. Если говорить о размещении школы, то вполне очевидно, что стоит учитывать количество детей, проживающих в каждом из населенных пунктов с тем, чтобы минимизировать суммарное пройденное ими всеми расстояние. Обобщая эти рассуждения, каждому объекту можно сопоставить некоторое число, называемое весом.

НЕОБХОДИМЫЕ УТОЧНЕНИЯ

Дан граф . Пусть – матрица кратчайших расстояний от i-й до j-й вершины, – весj-й вершины. Тогда можно определить понятие передаточного числа.

внешнее передаточное число:

,

внутреннее передаточное число:

Далее введем понятие медиан:

внешняя медиана графа - вершина , для которой

,

внутренняя медиана графа - вершина , для которой

.

Очевидно, что в случае неориентированного графа внешнее передаточное число равно внутреннему передаточному числу, и внешняя медиана совпадает с внутренней медианой.

Теперь, исходя из конкретной прикладной задачи, можно искать вершину, являющуюся внутренней или внешней медианой графа. Однако чаще всего смысл имеет поиск так называемой внешне-внутренней медианы графа, т.е. вершины, для которой сумма внутренних и внешних передаточных чисел будет наименьшей.

Возникает естественный вопрос: а что, если на каком-нибудь ребре графа (иными словами, на дороге между двумя обслуживаемыми объектами) существует точка y* такая, что искомое суммарное расстояние от нее до всех объектов и обратно будет меньше, чем для внешне-внутренней медианы? Оказывается, что оптимальная точка расположения пункта массового обслуживания обязательно совпадет с одним из обслуживаемых объектов.

Итак, в двухмерной сети для решения задачи размещения необходимо выбирать из N точек, что делает полный перебор легко осуществимым.

ОПИСАНИЕ АЛГОРИТМА

Основная идея

На основе исходных данных построить матрицу смежности. Пользуясь несколько раз алгоритмом Дейкстры, найти кратчайшие пути (выраженные явно или их приведенные эквивалентные характеристики) из каждой вершины в каждую. Затем, по очереди предполагая размещение пункта обслуживания в каждом объекте, рассчитать сумму произведений элементов соответствующей ему строки и столбца на вектор весов. Из найденных результатов отобрать минимальный.

Возможные сложности

Если моделью системы является ориентированный граф, рассматриваются пути до пункта обслуживания и обратно, и в качестве целевой функции используется минимизация стоимости обслуживания, то вполне возможна ситуация, когда затраты на проезд 1 км по пути к пункту обслуживания отличаются от затрат на проезд 1 км по пути обратно. В этом случае матрица кратчайших путей не будет отражать реальных финансовых затрат.

Способы преодоления

В таких случаях после нахождения матрицы кратчайших путей нужно последовательно для каждой вершины рассчитывать:

• сумму произведений элементов соответствующей ей строки на вектор весов с коэффициентом стоимости затрат на проезд из пункта обслуживания;

• сумму произведений элементов соответствующего столбца на вектор весов с коэффициентом стоимости затрат на проезд к пункту обслуживания.

ПРИМЕР ЗАДАЧИ

Семь деревень расположены так, как показано на рис. 8.1. Найти место для оптимального размещения школы, если в деревнях соответственно проживают 80, 100, 140, 90, 60, 50 и 40 детей школьного возраста. Критерий оптимальности – минимизация суммарного расстояния, проходимого всеми школьниками по пути в школу и обратно.

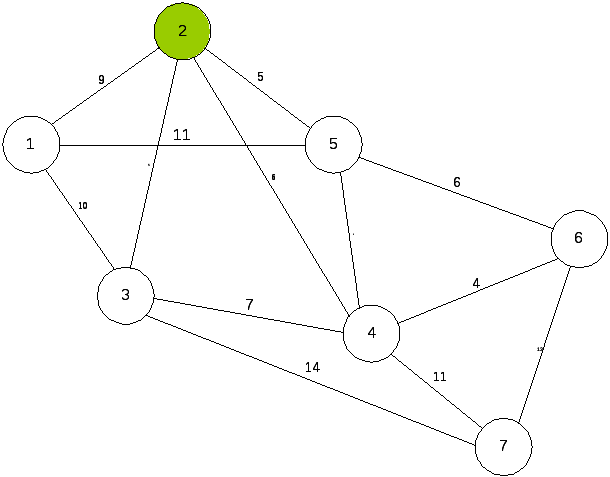
Рис. 8.1. Схема расположения объектов

Решая задачу описанным выше способом, получим, что школу нужно расположить в пункте 2.

ПРИМЕЧАНИЕ

Задачу можно обобщить на случай, если необходимо размещать не один, а P пунктов обслуживания. В этом случае постановка задачи выглядит так: разместить P пунктов обслуживания сети из N объектов так, чтобы сумма расстояний от каждого из объектов до ближайшего пункта обслуживания и обратно была минимальной. Соответствующее множество вершин называют P-медианой графа.

В этом случае простой перебор уже не дает эффективного решения. Для поиска P-медиан применяют методы целочисленного программирования, алгоритм направленного древовидного поиска, а также эвристический алгоритм Тэйца и Барта.