Загребаев Методы обработки статистической информации в задачах контроля 2008

Свойства оценок

Состоятельность. Оценка θ*( X1, ..., Xn ) называется состоя-

тельной, если по мере роста объема выборки n она сходится по вероятности к истинному значению параметра:

θ* (X	, ..., X )	n→∞	θ.
1	n	→
		по вероятности

Требование состоятельности отражает здравый смысл. Действительно, увеличение объема выборки есть не что иное, как увеличение информации о генеральной совокупности, поэтому оценка по выборке должна приближаться к истинному значению параметра. Это свойство оценки необходимо проверить в первую очередь. С другой стороны, свойство состоятельности – это асимптотическое свойство, т.е. оно может проявляться лишь при больших объемах выборки. Вместе с тем, как правило, можно предложить несколько состоятельных оценок одной и той же величины, которые при конечном объеме выборки будут давать различные результаты. Следовательно, только требования состоятельности недостаточно. Свойство оценки при конечном объеме выборки характеризует несмещенность.

Оценка θ*( X1, ..., Xn ) называется несмещенной, если при любом

объеме выборки n результат ее усреднения по всем возможным выборкам данного объема приводит к истинному значению оцени-

ваемого параметра, т.е. M[θ* ] = θ . В отличие от состоятельности,

несмещенность оценки характеризует ее доасимптотические свойства, т.е. хорошие или плохие свойства при конечном объеме выборки. Удовлетворение требованию несмещенности устраняет систематическую погрешность оценивания, которая зависит от объема выборки. Оценка может быть состоятельной, но смещенной, т.е. хорошей при n → ∞ , но плохой при конечном n.

Эффективность. Оценка θ*( X1, ..., Xn ) называется эффектив-

ной, если она при заданном объеме выборки имеет минимальную дисперсию. На рис. 1.17 показана такая ситуация.

61

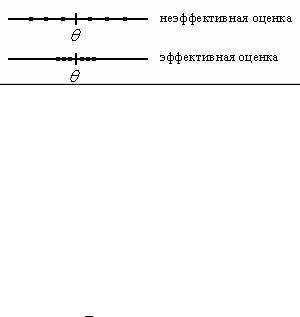
Рис. 1.17. Иллюстрация эффективности оценки

Отметим, что на практике стремятся, чтобы выбранная оценка удовлетворяла всем вышеперечисленным свойствам: состоятельности, несмещенности и эффективности.

Свойства средней выборочной. Пусть из генеральной сово-

купности в результате независимых наблюдений извлечена повторная выборка x1, ..., xn . Пусть генеральная средняя неизвестна и требуется ее оценить по данной выборке. Докажем, что если в качестве оценки выбрать среднюю выборочную xв , то эта оценка яв-

ляется несмещенной оценкой генеральной совокупности xг . Рассмотрим выборку в гипотетическом варианте, т.е. xв как

случайную величину Xв , а x1, ..., xn как X1, ..., Xn – соответст-

вующие независимые одинаково распределенные случайные величины. Так как эти величины имеют один и тот же закон распределения, совпадающий с законом распределения случайной величины X, то они имеют одинаковые числовые характеристики, в том числе математические ожидания.

M[X ] = M[X1] =... = M[Xn ] = a ;

M [ Xв] =	M [ X1 + X 2 +... + X n ]	=	1	M [ X + X +... + X ] =	1	na .
	n		n
					n

Таким образом, математическое ожидание средней выборочной совпадает с математическим ожиданием генеральной совокупности, т.е. оценка является несмещенной. В соответствии с предельной теоремой Чебышева эта оценка является и состоятельной. Действительно, по теореме Чебышева, при n → ∞ среднее арифметическое величин x1, ..., xn стремится к математическому ожиданию

M[ X ] = a , т.е. оценка является состоятельной.

62

Можно показать, что если X подчиняется нормальному закону, то оценка является и эффективной.

Свойство выборочной дисперсии. Пусть из генеральной сово-

купности в результате n независимых наблюдений над количественным признаком X извлечена повторная выборка объемом n. По данной выборке необходимо оценить неизвестную генеральную дисперсию. Казалось бы, что в качестве оценки следует взять выражение

				n
	1	n		∑xi
Dв =		∑(xi − xв)2 , где	xв =	i=1	,
				n
	n i=1

однако эта оценка является смещенной. Действительно, переходя к гипотетическому толкованию выборки, получим:

M[Dв] = M

1

n

в)2 .

∑(Xi − X

n i=1

Учтем, что M[Xi ] = M [Xв] = mx , тогда

в − mx ,

Xi = X − mx , Xв = X

в)2 = ( Xi − Xв)2 ,

( Xi − X

1

n

1 n

Dв

=

− Xв)2 =

∑(Xi

∑(Xi − Xв)2 =

n i=1

n i=1

n

1

n

n

1

n

∑Xi

i=1

=

∑Xi2

− 2Xв∑Xi

+ nXв2 =

∑Xi2 − 2Xв

+ Xв ,

n

n

i=1

i=1

n i=1

n

n

M[Dв] =

1 M ∑Xi2 − M[Xв2

] = 1 ∑D[Xi ] − D[Xв] =

n

i=1

n i=1

= 1n nDг − Dnг = nn−1 Dг .

Таким образом, несмещенная оценка для генеральной средней будет

63

		n			1	n
	Dг =			Dв =		∑(xi − xв)2 = s2 .	(1.2.7)
		n −1
					n −1i=1

Величина s2 носит название исправленной выборочной. Легко видеть, что исправленная выборочная дисперсия является состоятельной оценкой генеральной дисперсии.

Асимптотические свойства оценки. Всякая оценка

θ* ( X1, ..., Xn ) как функция от «гипотетических» результатов на-

блюдения является случайной величиной и, следовательно, ее свойства определяются функцией распределения. Причем, закон

распределения оценки θ* зависит от объема выборки n. Получение закона распределения оценки для данного объема выборки n является очень сложной задачей, поэтому обычно пользуются асимптотическим законом распределения оценок, т.е. при n → ∞ . В этом случае говорят об асимптотической несмещенности и асимптотической эффективности оценки.

Из асимптотической несмещенности оценки не следует ее несмещенность в обычном смысле и наоборот. На практике асимптотическая дисперсия оценки обычно оказывается меньше, чем дисперсия в обычном смысле.

Если есть θ1* и θ*2 – две различные, асимптотически несмещенные, оценки параметров θ, то оценка θ1* называется более эффективной, чем θ*2 , если D1 < D2 .

Метод максимального правдоподобия. Определение неизвестных параметров нормального закона распределения

Пусть из генеральной совокупности извлечена выборка объемом n. Известно, что закон распределения наблюдаемой случайной величины X описывается плотностью распределения f (x, θ) , где θ –

параметр распределения. Если рассматривать выборку в гипотетическом смысле, то X1, ..., Xn – независимые одинаково распределенные случайные величины. Тогда для любого реализованного значения выборки x1, ..., xn плотность распределения есть

64

L(x1, ..., xn ; θ) = f (x1, θ) f (x2 , θ) ... f (xn , θ) . Таким образом,

L(x1, ..., xn ; θ) задает вероятность получения при извлечении выборки объема n именно наблюдений x1, ..., xn . Поэтому, чем больше L, тем правдоподобнее выборка x1, ..., xn . Потребуем подобрать

неизвестный параметр распределения θ так, чтобы реализованная выборка была наиболее правдоподобной, т.е. чтобы функция правдободобия L, достигала максимального значения: найдем

	max L(x1, ..., x2 ; θ) .				(1.2.8)
	θ
	Если L(x1, ..., xn ; θ) – дифференцируемая функция,				то условие
	максимума есть
	∂L	= 0,	∂2 L	< 0 .	(1.2.9)
	∂θ		∂θ2

Пример 1.1. Пусть случайная величина X распределена в генеральной совокупности по нормальному закону. Оценить по данным

выборки x1, ..., xn

математическое ожидание и дисперсию,

т.е. не-

известные параметры нормального закона.

1

−(x−mx )2

2

2σ2x

f (x,θ) = f (x,θ1, θ2 ) = f (x, mx , σx )

=

σx

2π

l

.

Построим функцию правдоподобия:

L(x1, ..., xn ; θ) = f (x1, θ)

f (x2 , θ) ...

f (xn , θ) ;

(1.2.10)

( x −m

x

)2

(x −m

x

)2

1

−

1

1

−

n

; σ2 ) =

2σ2x

2σ2x =

L(x

, ..., x

; m

x

l

×... ×

l

1

n

x

σx

2π

σx 2π

n

(x −m

x

)2

1

−∑

i

l

2σ2

=

i=1

x .

(σx 2π)n

Учитывая, что соотношения

∂L

= 0

и

∂ln L

= 0

равносильны, а

∂θ

∂θ

корни последнего уравнения найти проще, получим:

65

		1				1	n	(x	− m	)2
ln L = ln					−		∑	i	x		.
	(σx	2π)	n			2			2
						2σx	i=1		2σx

Оценки для математического ожидания и дисперсии находятся из соотношений:

∂ln L = 0;

∂m

x (1.2.11)

∂ln L = 0.∂σ2x

Раскрывая выражения (1.2.11) в явном виде, получим:

∂ln L		1	n
	=		∑(xi − mx ) = 0 .
∂m x
		σ2x i=1

Из этого выражения следует формула для оценки математического ожидания:

				n
				∑xi
		mx =		i=1		.
		∂2 ln L		n
	Легко показать, что		= −		n			< 0	, т.е. находится действи-
		∂mx2			σ2x

тельно максимум функции. Для оценки дисперсии получим

σ2x = 1n ∑n (xi − mx )2 . i=1

Таким образом, для математического ожидания мы получили эффективную, состоятельную, несмещенную оценку, а для дисперсии – смещенную оценку.

Пример 1.2. Пусть известно, что случайная величина X подчи-

нена закону Пуассона, P(X = x) = λxl−λ . Пусть на практике полу- x!

чен следующий результат: в первой серии, состоящей из n наблюдений событие A, произошло x1 раз, во второй серии – x2 раз и

66

т.д., в n-й серии – xn раз. Требуется по выборке x1, ..., xn оценить параметр закона распределения, т.е. λ:

L(x

, ..., x

; θ) = P(x ) P(x

2

) ×... × P(x

n

) =

λx1l−λ

λx2 l−λ

...

λxn l−λ

.

1

2

1

x1

!

x2 !

xn !

Возьмем натуральный логарифм от функции правдоподобия:

n

∑xi

−λn

n

n

n

λ

i=1

l

∑ xi

ln L = ln

= ln λi=1 l−λn − ln x !... x

! =

∑ x ln λ −λn −

∑

ln(x !) .

x !...x !

i

n

i=1 i

i

i

n

i=1

Из условия нахождения экстремума

∂ln L

= 0 , получим

∂λ

n

∑xi

λ =

i=1

.

(1.2.12)

n

Выражение (1.2.12) показывает смысл постоянной в законе Пуассона (λ – математическое ожидание).

Метод моментов. Примеры оценки по методу моментов

Суть данного метода заключается в приравнивании определенного количества выборочных моментов к соответствующим теоретическим. Количество приравниваемых моментов равно числу неизвестных параметров закона распределения. В качестве моментов могут рассматриваться как начальные, так и центральные моменты.

Математическая формулировка такова:

	1 n
∫x(l) f (x, θ)dx =		∑xi(l) .	(1.2.13)
	n i=1
Пример 1.3. По выборке x1, ..., xn	требуется найти оценку неиз-
вестного параметра λ показательного распределения			f (x) =λl−λx

(x ≥0) . Так как требуется найти только один параметр, то необходимо одно уравнение для моментов ( l =1):

67

∞		−λxdx =		1 n
∫ xλl
						∑xi .
0				n i=1
∞						1
Можно показать, что ∫ xλl−λxdx =							, таким образом
0						λ
			n
1			∑xi
		=	i=1		= x .			(1.2.14)
	λ		n				в

Пример 1.4. По выборке x1, ..., xn найти методом моментов для

нормального закона распределения mx и σ2x .

1. Так как по определению математическое ожидание является первым моментом, получим:

	+∞			1	n
	mx = ∫ x f (x, mx , σ2x )dx =					= xв .	(1.2.15)
					∑xi
	−∞			n i=1
	2. По определению дисперсии
	+∞	1	n
	Dx = ∫ (x − mx )2 f (x, mx , σ2x )dx =						(1.2.16)
			∑(xi − xв)2 = Dв .
	−∞	n i=1

Из вышеприведенных примеров видно, что оценки по методу моментов получить достаточно просто и выражаются они через эмпирические моменты, что упрощает исследование статистических свойств оценок. Однако, эффективность оценок, полученных по методу моментов иногда ниже, чем полученных, исходя из принципа максимального правдоподобия. Зачастую оценки по методу моментов используют для определения начальных, приближенных оценок, которые в дальнейшем уточняются другими методами.

Интервальное оценивание

Рассмотренные ранее методы оценивания неизвестного параметра θ позволили нам получить оценку, выраженную одним числом – как говорят, «точечную» оценку. При этом, вычисляя оценку

θ* на основании имеющейся выборки x1, ..., xn , понимаем, что та-

68

кая оценка является лишь приближением к истинной величине па-

раметра θ. Так как оценка θ* случайна, возникает вопрос, насколько она отличается от истинного значения θ. Можно ли указать такую величину , которая с практической достоверностью гаранти-

ровала бы выполнение неравенства θ − θ* < . Иначе говоря, нель-

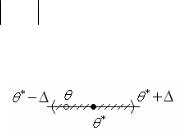
зя ли указать такой интервал вокруг θ* , который с заданной вероятностью накрывал бы истинное значение θ (рис. 1.18)?

Рис. 1.18. Геометрическая иллюстрация понятия интервальной оценки

При этом вероятность, заранее выбираемая исследователем, с которой интервал (θ* − , θ* + ) накрывает истинное значение θ называется доверительной вероятностью и обозначается β, а сам интервал (θ* − , θ* + ) – доверительным интервалом.

Математически требование того, чтобы истинное значение оцениваемого параметра находилось с вероятностью β внутри доверительного интервала, выражается так:

P(

θ* − θ

< ) = β.

(1.2.17)

Интервал (θ* − , θ* +Δ) случаен по своей природе как по своему расположению на числовой оси, так и по своей длине, поскольку

θ* и находятся на основании выборочных случайных значений x1, ..., xn . Ширина доверительного интервала зависит от объема выборки: при увеличении объема выборки ( n → ∞ ) величина доверительного интервала уменьшается ( →0 ). Величина интервала зависит также и от доверительной вероятности β: при β →1 → ∞ .

Интервальным оцениванием пользуются при небольших объемах выборки. Если оценивается не один параметр, то говорят о доверительной области. Решение задачи о нахождении доверительного интервала по заданной доверительной вероятности не представляла бы трудностей, если был известен закон распределения оценки,

69

например, в форме плотности распределения f (θ* ) . Действительно, в этом случае из решения уравнения

	θ*+Δ
	∫ f (θ* )dθ* = β
	θ*−
можно было бы найти	или, наоборот, при заданном	найти веро-
ятность β попадания	истинного значения параметра	в интервал

(θ* − , θ* + ) . К сожалению, функция плотности распределения оценки, как правило, не известна. Из положения выходят следую-

щим образом. Формируют некоторую функцию от оценки θ* , т.е. производный параметр, распределение которого хорошо известно. Находят для него доверительный интервал, а затем делают обратное преобразование и находят доверительный интервал для искомой оценки. При этом часто используются, например, законы распределения Стьюдента и Пирсона.

Распределение Стьюдента. Если случайная величина X распределена в генеральной совокупности по нормальному закону с

параметрами mx и σ2x , то в гипотетическом варианте каждая из случайных величин X1, ..., Xn , подчиняется нормальному закону с

теми же				параметрами, следовательно,		и их			линейная функция
			n
			∑Xi
		в =	i=1		также распределена по нормальному закону с матема-
X
			n
							Dx
тическим ожиданием mx и дисперсией								.	Действительно, ис-
							n

пользуя теоремы о числовых характеристиках, получим:

				n			n
				∑Xi			∑M[Xi ]		n mx
			в] = M	i=1		=	i=1	=		= mx ; (1.2.18)
	M[X
				n			n
									n

70