Загребаев Методы обработки статистической информации в задачах контроля 2008

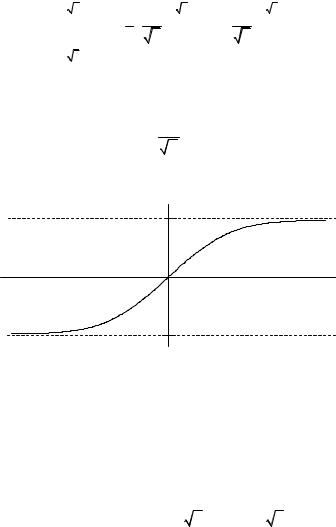
β−mx

β−mx

α−mx

σx

2

−t2

1

2

σx

2

−t2

2

σx 2

−t2

P(α< X <β) =

∫

l

dt =

∫

l

dt −

∫

l

. (1.1.41)

2

π

π

dt

α−mx

0

0

σ

x

2

Выражение (1.1.41) можно переписать короче, если ввести в

рассмотрение так называемую функцию Лапласа

2

x

Φ(x)

=

∫l−t2 dt .

(1.1.42)

π

0

Вид функции Лапласа показан на рис. 1.11.

Φ(x)

1

0

x

-1

Рис. 1.11. Функция Лапласа

Из рисунка видно, что

Φ(0) = 0; Φ(−x) = −Φ(x); Φ(+∞) =1; Φ(−∞) = −1 .

Вероятность попадания случайной величины в интервал (α, β) есть:

1

β − m

α − m

P(α < X < β) =

x

x

. (1.1.43)

Φ

− Φ

2

σ

2

σ

2

x

x

На рис. 1.10 показан геометрический смысл этого выражения как площади под колоколообразной кривой, ограниченной прямыми x = α и x = β .

31

Вероятное отклонение. Правило 3σ

Часто требуется найти такой интервал E около математического ожидания, вероятность попадания в который равна заданной величине, например ε. Для нахождения этой вероятности воспользуемся

соотношением (1.1.43), в котором положим α = mx − E;				β = mx + E .
Тогда после несложных преобразований получим:
	E
ε = Φ			.	(1.1.44)
	σx	2

Для заданного ε по таблицам значений функции Лапласа нахо-

дим аргумент	E	, при котором		E			= ε . Допустим
			Φ
	σx 2			σx	2

	E		= γ ,	тогда E = γσx 2 . Например, пусть	ε = 0,5 , тогда по
	σx	2
таблицам				Лапласа находим γ = 0, 477 и,	следовательно,

E = 0,675σx . Таким образом, с вероятностью 50 % значения случайной величины X, подчиненной нормальному закону, попадают в интервал (mx − 0,675σx , mx + 0,675σx ) . Величина E = 0,675σx при

этом называется вероятным отклонением.

Поставим теперь задачу по-другому. Пусть требуется определить вероятность попадания в заданный интервал E, симметричный около математического ожидания. Будем измерять E в единицах среднего квадратического отклонения. Тогда получим:

E = σ

P(m

X < m

σ

x

1

;

x

;

x

− σ

x

<

x

+ σ

x

)

= Φ

= Φ

= 0,677

σx

2

2

2σ

2

E=2σ ;

P(m −2σ <X <m +2σ )=Φ

x

=Φ

=0,953;

σ

2

x

x

x

x

x

2

x

3σ

3

E =3σ ; P(m −3σ < X <m +3σ ) =Φ

x

=Φ

=0,997 .(1.1.45)

σ

2

2

x

x

x

x

x

x

32

Из выражения (1.1.45) видно, что с вероятностью, почти равной единице, значение случайной величины попадет в интервал (mx −3σx , mx + 3σx ) . Иначе говоря, при нормальном законе рас-

пределения почти все значения случайной величины не уклоняются от математического ожидания больше, чем на 3σx . Отсюда следу-

ют такие практические выводы.

1. Если известно, что случайная величина распределена по нормальному закону и дано некоторое множество ее значений, то σx приблизительно можно определить, разделив разницу между мак-

симально удаленным значением и средним на 3, т.е. σx ≈ xmax − x . 3

2. По множеству значений случайной величины приближенно

		N		N
		∑(xi − x)2		∑xi
	находят σx ≈	i=1	, где x =	i=1
		N −1		N

Если самая удаленная точка отличается от среднего значения не более, чем на 3σx , то закон распределения можно принять за нор-

мальный (конечно, в дальнейшем следует провести дополнительные исследования).

Система случайных величин

На практике часто встречается необходимость описывать объекты, которые характеризуются не одной, а несколькими случайными величинами, образующими комплекс или систему. При этом связь между величинами носит стохастический характер. При этом свойства системы случайных величин не исчерпываются свойствами отдельных величин, её составляющих, помимо этого они включают также взаимные связи между случайными величинами.

Система двух ( X , Y ) или более (X1, ..., Xn ) случайных величин

может быть изображена случайной точкой, соответственно, в двухмерном или n-мерном пространстве.

33

Функция распределения системы двух случайных величин
Функцией распределения двух случайных величин называется ве-
роятность совместного выполнения двух неравенств –		X < x	и
Y < y :
F(x, y) = P((X < x)(Y < y)) .		(1.1.46)
Свойства функции распределения следуют из ее геометрической
интерпретации (рис. 1.12).
y1
F (x1, y1)
y2
F (x2 , y2 )
	x
x1	x2
Рис. 1.12. Геометрическая интерпретация функции распределения
системы двух случайных величин

Свойства функции F (x, y) .

1. Функция распределения системы случайных величин – неубывающая функция. Это означает, что если x2 > x1 , то

F(x2 , y) ≥ F(x1, y) , если y2 > y1 , то F(x, y2 ) ≥ F(x, y1) .

2.F (x, −∞) = F (−∞, y) = F (−∞, −∞) = 0 .

3.F(x, +∞) = F1(x); F(+∞, y) = F2 ( y) .

4.F (+∞, +∞) =1.

Условимся событие, состоящее в том, что случайная точка попадет в область R, обозначать ( X ,Y ) R .

34

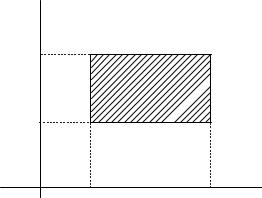
Найдём вероятность попадания точки в область в виде прямоугольника со сторонами, параллельными координатным осям

(рис. 1.13):

P((X ,Y ) R) = F(β,δ) − F(α,δ) − F(β, γ) + F(α, γ) . (1.1.47)

В выражение (1.1.47) последний член входит со знаком «плюс», потому что при вычитании F (α,δ) и F (β, γ) мы два раза вычитаем

площадь F(α, γ) .

Пусть теперь область R представляет собой элементарный прямоугольник с площадью S = x y (см. рис. 1.13).

δ

R

γ

αβ

Рис. 1.13. Иллюстрация к выводу функции плотности распределения системы двух случайных величин

Вероятность попадания случайной точки в эту элементарную площадку есть

P((X,Y) R) =F(x+Δx, y+Δy)−F(x+Δx, y)−F(x, y+Δy)+F(x, y). (1.1.48)

Для непрерывных случайных величин существует предел

lim	P(( X ,Y ) R)		=	∂2F(x, y)	= f (x, y) .	(1.1.49)
		x y		∂x∂y
x→0
y→0
Функция f (x, y)		называется плотностью распределения систе-

мы двух случайных величин. По своему смыслу f (x, y)dxdy есть

35

вероятность попадания случайной величины в элементарную площадку dS = dxdy . Понятно, что вероятность попадания случайной

точки в произвольную область R есть

P((X ,Y ) R) = ∫∫ f (x, y)dxdy .	(1.1.50)
R

Между функцией распределения и плотностью распределения существует простая связь:

x	y
F (x, y) = ∫	∫ f (x, y)dxdy .	(1.1.51)

−∞ −∞

В справедливости этого выражения легко убедиться, если взять смешанную производную по переменному верхнему пределу. Тогда получим выражение (1.1.49).

Свойства функции плотности распределения f (x, y) вытекают

из свойств функции распределения F (x, y) :
1.	Так как F (x, y) – неубывающая функция, а	f (x, y) – ее про-
изводная, то f (x, y) ≥ 0 .
2.	Так как F (+∞, + ∞) =1, то из выражения	(1.1.51) следует
+∞ +∞	f (x, y)dxdy =1.
∫ ∫

−∞ −∞

Законы распределения случайных величин, входящих в систему.

Условные законы распределения

Понятно, что должна существовать связь и между такими функциями как плотность распределения системы f (x, y) и плотностя-

ми распределения отдельных переменных f1(x) и f2 ( y) .

Теорема. Пусть f (x, y) – плотность распределения системы случайных величин ( X ,Y ) , тогда плотность распределения от-

+∞	+∞
дельных величин есть f1(x) = ∫	f (x, y)dy и f2 ( y) = ∫ f (x, y)dx
−∞	−∞

36

Данная теорема показывает, что, зная закон распределения системы величин, можно определить закон распределения каждой из них, но обратное утверждение, вообще говоря, неверно. Недостаточно знать закон распределения каждой величины, необходимо знать зависимость между величинами, входящими в систему. Эта зависимость может быть охарактеризована с помощью условных законов распределения.

Условным законом распределения случайной величины X, вхо-

дящей в систему ( X ,Y ) называется закон её распределения, вычис-

ленный при условии, что случайная величина Y приняла определённое значение.

Теорема. Закон распределения системы случайных величин ( X ,Y ) можно представить в виде

f (x, y) = f1(x) f ( y / x) или f (x, y) = f2 ( y) f (x / y) . (1.1.52)

Определение. Случайные величины X и Y называются независимыми, если закон распределения каждой их них не зависит от того, какое значение приняла другая величина. Условие независимости записывается следующим образом:

f (x / y) = f1(x) – случайная величина X не зависит от случайной величины Y;

f ( y / x) = f2 ( y) – случайная величина Y не зависит от случай-

ной величины X.

Зависимость или независимость случайных величин всегда взаимны.

Для независимых случайных величин плотность распределения системы равна произведению плотностей распределений отдельных величин:

f (x, y) = f1(x) f2 ( y) .

(1.1.53)

Числовые характеристики системы двух случайных величин

Важнейшими числовыми характеристиками системы двух случайных величин являются следующие: mx = M[X ] , my = M[Y ] ,

Dx = M[(X )2 ] , Dy = M[(Y )2 ] . Смысл этих величин понятен и ни-

37

чем не отличается от смысла числовых величин, рассмотренных ранее для одной переменной. Но эти числовые характеристики никак не отражают того факта, что случайные величины X и Y образуют систему случайных величин ( X ,Y ) . Характеристикой именно

системы случайных величин является ковариационный момент Kxy , который по определению есть

Kxy = M[( X − mx )(Y − my )] .

(1.1.54)

Ввиду особой важности этой характеристики приведем ее явный вид для дискретных и непрерывных величин:

Для дискретных случайных величин

	n n
Kxy = ∑∑(xi − mx )( y j		− m j ) pij .	(1.1.55)
	i=1 j=1
Для непрерывных случайных величин
+∞ +∞
Kxy = ∫ ∫	(x − mx )( y − my ) f (x, y)dxdy .		(1.1.56)
−∞ −∞
Y	Y

X	X
а)	б)

Рис. 1.14. Распределение точек на плоскости

при различных значениях ковариационного момента: а) Kxy > 0; б) Kxy > 0

На рис. 1.14 показано распределение случайных точек на плоскости при различных значениях ковариационного момента. Из рисунка видно, что чем больше ковариационный момент между случайными величинами ( X ,Y ) , тем теснее располагаются точки друг

к другу. Однако ковариационный момент характеризует не только

38

степень «тесноты» зависимости между X и Y, но и их рассеяние. Действительно, если X мало отличается от mx , то Kxy будет бли-

зок к нулю, хотя случайные величины X и Y могут быть и сильно связаны. Поэтому для характеристики именно степени связи между X и Y вводится безразмерная величина

r =	Kxy				.	(1.1.57)
	σ		σ
xy		x		y
Величина rxy называется	коэффициентом					корреляции. Если

rxy = 0 , то случайные величины называются некоррелированными.

Отметим сразу, что некоррелированность в общем случае не означает независимости случайных величин. В тоже время из независимости некоррелированность следует. Действительно, если X и Y

независимы, то f (x, y) = f1(x) f2 ( y) , тогда

	+∞ +∞
Kxy	= ∫ ∫ (x − mx )( y − my ) f (x, y)dxdy =
	−∞ −∞
+∞ +∞
= ∫	∫ (x − mx )( y − my ) f1(x) f2 ( y)dxdy =
−∞ −∞
+∞	+∞

= ∫ (x − mx ) f1(x)dx ∫ ( y − my ) f2 ( y)dy = 0.

−∞ −∞

Коэффициент корреляции характеризует степень тесноты линейной зависимости. Можно показать, что если между случайными величинами есть функциональная зависимость Y = a X +b , то rxy = +1 , если a > 0 и rxy = −1 , если a < 0 . В общем случае, когда X

и Y связаны вероятностной зависимостью, то −1< rxy <1.

Числовые характеристики системы n случайных величин

Система случайных величин (X1, ..., Xn ) может быть охарактеризована следующим минимальным числом характеристик:

1) n математических ожиданий m1, ..., mn ;

39

2) n дисперсий;

3) n (n −1) корреляционных моментов Kij = M[Xi X j ] , где i ≠ j .

Ковариционные моменты образуют симметричную положительно определенную матрицу

ˆ		K	... K
		11	1n
K =			...	.
	Kn1		... Knn

Для некоррелированных случайных величин матрица		ˆ
		K диаго-
нальна. Два случайных вектора X и Y называются некоррелиро-
ванными, если каждая из составляющих вектора	X некоррелиро-
вана с каждой из составляющих вектора Y , т.е.	Kij = 0	для всех
i =1, ..., n и j =1, ..., n .

Нормальный закон распределения системы двух случайных величин (нормальный закон на плоскости)

Из законов распределения случайных величин рассмотрим наиболее распространенный – нормальный. Для наглядности ограничимся случаем системы из двух случайных величин, поскольку она может представляться случайной точкой на плоскости. Функция плотности распределения системы в этом случае выражается формулой:

	1		1		,	(1.1.58)
f (x, y) =		exp −		Q(x, y)
			2
	2πσxσy 1− r2

где

Q(x, y) =		1		(1− m	x	)2
		− r2		σ2
1
				x

	2r(x − mx )( y − my )				(1	− my )2
−				+			. (1.1.59)
	σ	σ				σ2
			y
	x					y

40