Загребаев Методы обработки статистической информации в задачах контроля 2008

Функция распределения случайной величины Х есть

+∞		1				−	(x−mx )2
										.	(1.1.60)
f1(x) = ∫	f (x, y)dy =				l			2σ2x
		σx	2π
−∞
Функция распределения случайной величины Y есть
+∞		1				−		( y−my )2
								2σ2y		.	(1.1.61)
f2 ( y) = ∫	f (x, y)dx =				l
		σy	2π
−∞
Можно показать, что
+∞ +∞
Kxy = ∫ ∫ (x − mx )( y − my ) f (x, y)dxdy = rσxσy .											(1.1.62)

−∞ −∞

Нетрудно видеть, что при некоррелированных случайных величинах, т.е. при r = 0 , выражение для плотности распределения системы имеет вид:

1

−

(x−mx )

2

1

−

( y−my )2

2σ2y = f (x) f

f (x, y) =

l 2σ2x

l

2

( y) . (1.1.63)

σx

2π

σy

2π

1

Из формулы (1.1.63) видно, что при нормальном законе распределения случайных величин из некоррелированности следует их независимость.

Если случайные величины коррелированны ( r ≠ 0 ), то можно найти условные законы распределения:

1

y−my

(x−mx )

2

f (x, y)

1

−

−r

2(1−r2 )

σy

σ

f ( y / x) =

=

l

x

;

(1.1.64)

f1

(x)

σy 2π 1− r2

1

( x−mx )

y−my

2

f (x, y)

1

−

−r

2(1−r2 )

σ

σy

f (x / y) =

=

l

x

.

(1.1.65)

f2

( y)

σx 2π 1− r2

41

Формулу (1.1.64) можно привести к виду

					1		σy	2
		1		−		y−my −r		(x−mx )
							σx
f ( y / x) =				l	2(1−r2 )σy				. (1.1.66)
	σy	2π	1− r2
Легко видеть,		что	f ( y / x)		есть плотность распределения слу-

чайной величины, имеющей нормальный закон распределения, если положить

	my/ x = my + r	σy	(x − mx ) ,	(1.1.67)
		σy
	σy/ x = σy	1− r2 .		(1.1.68)

Из этих формул видно, что от x зависит только математическое ожидание, но не дисперсия. При этом my/ x есть условное матема-

тическое ожидание. В геометрическом плане выражение (1.1.67) представляет собой линию, которая называется линией регрессии случайной величины Y на X.

Числовые характеристики функций случайных величин

На практике часто возникает необходимость определять статистические характеристики функции от случайных величин. В математическом плане задача ставится следующим образом. Случайная величина Y есть неслучайная функция нескольких случайных величин Y = ϕ(X1, ..., Xn ) . Известны математические ожидания и дис-

персии аргументов: mx1 , ..., mxn и Dx1 , ..., Dxn . Требуется определить математическое ожидание и дисперсию функции

M[ϕ( X1, ..., Xn )] = mϕ и D[ϕ(X1, ..., Xn )] = Dϕ . (1.1.69)

Обобщая вышеприведенные формулы на функцию многих случайных аргументов, например, для непрерывных случайных величин получим:

M[ϕ(X1, ..., Xn )] = mϕ =

42

	+∞	+∞
= ∫ ... ∫ ϕ(x1, ..., xn ) f (x1, ..., xn )dx1 ... dxn ;			(1.1.70)
	−∞	−∞
		D[ϕ( X1, ..., X n )] = Dϕ =
+∞	+∞
= ∫ ... ∫ [ϕ(x1, ..., xn ) − mϕ]2 f (x1, ..., xn )dx1 ... dxn .			(1.1.71)
−∞	−∞

Примечательным в приведенных выше выражениях является то,

что для определения числовых характеристик функций случайных аргументов достаточно знать только закон распределения аргу-

ментов. Более того, если функция линейно зависит от своих аргументов, то знать закон их распределения тоже не обязательно. Для определения числовых характеристик в этом случае достаточно знать только числовые характеристики самих аргументов. Нетрудно показать справедливость следующих соотношений.

1. Математическое ожидание постоянной величины есть сама эта величина

M[c] = c .	(1.1.72)
2. Дисперсия неслучайной величины равна нулю
D[c] = 0 .	(1.1.73)

3. Неслучайная величина может быть вынесена за знак математического ожидания

M[cX ] = cM [X ] .

(1.1.74)

4. Вынесение не случайной величины за знак дисперсии и среднего квадратического отклонения

D[cX ] = c2D[X ]; σ[cX ] =		c		σ[X ] .	(1.1.75)

5. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий:

M[X +Y ] = M[X ] + M[Y ] .

(1.1.76)

6. Математическое ожидание линейной функции от случайных аргументов равно линейной функции от математических ожиданий аргументов:

43

n	n
M[∑ai Xi + b] = ∑aimx			+ b .	(1.1.77)
i=1	i=1	i

7. Дисперсия суммы случайных величин

D[X +Y ] = D[X ] + D[Y ] + 2 Kxy .				(1.1.78)
8. Дисперсия линейной функции
n		n	∑aia j Kij .	(1.1.79)
D ∑ai Xi + b		= ∑ai2 D[Xi ] + 2
i=1	i=1		i< j

для некоррелированных случайных величин

n		n
D ∑ai Xi +b		= ∑ai2 D[Xi ] .
i=1		i=1

Приведенные правила еще раз подчеркивают важное свойство математического ожидания как линейного оператора. Перечислим еще ряд полезных соотношений для нелинейной функции – произведения случайных величин:

математическое ожидание произведения случайных величин

M[X Y ] = M[X ] M[Y ] + Kxy .

(1.1.80)

дисперсия произведения независимых случайных величин

D[XY ] = D[X ]D[Y ] + mx2D[Y ] + m2y D[X ].

(1.1.81)

Метод линеаризации функции случайных аргументов

Рассмотренный ранее аппарат числовых характеристик позволяет определять числовые характеристики функций случайных аргументов, зная лишь числовые характеристики самих аргументов. В этом заключается его удобство. Однако применим этот аппарат, главным образом, к линейным функциям. Если исходная функция нелинейна, то выйти из положения можно следующим образом.

Допустим, что значения случайной величины X ограничены пределами α и β, а случайная величина Y связана со случайной величиной X функциональной зависимостью

Y = ϕ(X ) .

(1.1.82)

44

Разложим функцию Y в ряд около точки mx и ограничимся членами первого порядка малости:

	Y ≈ ϕ(mx ) +	dϕ		(X − mx ) .	(1.1.83)
		dx
				x = mx

Чем меньше интервал (α, β) , тем точнее выполняется соотно-

шение (1.1.83). Так как теперь функция Y является линейной относительно аргумента X, то для нахождения ее математического ожидания и дисперсии можно применить аппарат числовых характеристик.

M[Y ] = M[ϕ(mx ) + dϕ

( X − mx )] =

= M[ϕ(mx )] + dϕ

dx

x = mx

M[(X − mx )] = ϕ(mx ) ;

dx

x = mx

2

D[Y ] = D[ϕ(mx )] +

dϕ

D[(X − mx )] =

dx

x = mx

dϕ

2

D[X ].

=

dx

x = mx

(1.1.84)

(1.1.85)

Этот подход легко обобщается, когда Y является функцией многих переменных:

Y = ϕ( X1, ..., Xn ) .

(1.1.86)

Тогда функцию Y = ϕ( X1, ..., Xn ) также раскладывают в ряд и ограничиваются линейным членом:

n

Y≈ ϕ(mx1 , ..., mxn ) + ∑ϕ′xi (mx1 , ..., mxn )(Xi − mxi ) . (1.1.87)

i=1

Применяя аппарат числовых характеристик, получим:

M[Y ] = ϕ(mx	, ..., mx ) ;	(1.1.88)
1	n

45

n

dϕ

2

dϕ

D[Y ] = ∑

D[X ] + 2∑

dϕ

Kij , (1.1.89)

dx

dx

i=1

i< j

dx

j

i

i

ˆ

K

... K

11

1n

где K =

...

– ковариционная матрица аргументов.

Kn1

... Knn

Если при разложении функции в ряд оставить еще одно слагаемое:

Y ≈ ϕ(mx ) + dϕ				(X − mx ) +	1 d 2ϕ	(X − mx )2 , (1.1.90)
dx		x = m	x		2 dx2	x = mx

то результаты линеаризации можно уточнить. Действительно, применяя к выражению (1.1.90) операцию нахождения математического ожидания, получим:

	M[Y ] = ϕ(mx ) +	1 d 2ϕ	D[ X ] .	(1.1.91)
		2 dx2
			x = mx

Поправка к дисперсии просто выглядит, когда случайная величина, распределенная по нормальному закону:

dϕ				2		1	d 2ϕ
D[Y ] =					D[X ] +
	dx		x = m			2	dx2
				x

2

D2[X ] .

x = mx

Возможно, конечно, обобщение данных результатов на многомерный случай, однако формулы в этом случае выглядят очень громоздкими.

Закон распределения функций случайных аргументов

Рассмотренные выше способы получения статистических характеристик функции от случайных аргументов имеют недостатки. Вопервых, они справедливы лишь для линейных функций. Если же функция нелинейная и используется метод линеаризации, то трудно оценить ошибку определения числовых характеристик. Знание

46

закона распределения функции решает все эти проблемы. Действительно, если задана функция Y = ϕ( X ) и известна плотность рас-

пределения случайной величины Y, которую мы обозначим g( y) , то числовые характеристики функции Y = ϕ( X ) могут быть найдены из следующих соотношений:

+∞
M[Y ] = my = ∫ y g( y)dy ;	(1.1.92)
−∞
+∞
D[Y ] = Dy = ∫ ( y − my )2 g( y)dy .	(1.1.93)

−∞

Можно показать, что если плотность распределения аргумента

	есть функция f (x) , то плотность распределения g( y)				есть
		dψ( y)		,	(1.1.95)
	g( y) = f (ψ( y))
		dy
	где ψ( y) – функция обратная функции y = ϕ(x) .

Идею получения закона распределения для функции нескольких аргументов покажем на примере функции двух случайных величин.

Закон распределения функции двух случайных величин

Пусть имеется система двух случайных величин (X , Y ) с плотностью распределения f (x, y) и случайная величина Z, связанная с (X , Y ) функциональной зависимостью Z = ϕ( X , Y ) . Требуется оп-

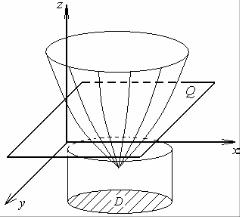
ределить закон распределения случайной величины Z. На рис. 1.15 показана функция Z = ϕ( X , Y ) . Плоскость Q, параллельная плоско-

сти XOY , осуществляет сечение этой функции на высоте z. Область D есть проекция этого сечения на плоскость XOY .

Как следует из рисунка, если случайная точка (X , Y ) попадает в область D, то ϕ(X , Y ) < z . Таким образом, вероятность того, что значение случайной функции будет менее величины z , есть веро-

47

ятность попадания случайной точки в область D, т.е. функция распределения случайной величины Z = ϕ( X , Y ) есть

G(z) = P(Z < z) = P(ϕ(X , Y ) < z) = P((X , Y ) D) ;

G(z) = P((X , Y ) D) = ∫ ∫ f (x, y) dxdy .

D( z)

Рис. 1.15. Иллюстрация к закону распределения двух случайных величин

Величина z в это выражение входит через предел интегрирования. Дифференцируя G(z) по z, получим плотность распределения

случайной величины Z.

Закон распределения суммы двух случайных величин. Композиция законов распределения

Пусть имеется система двух случайных величин (X , Y ) с плотностью распределения f (x, y) . Требуется найти закон распределения случайной величины Z = X +Y . Поверхность z = x + y –

плоскость, проходящая через начало координат (рис. 1.16). В заштрихованной области лежат те значения аргументов, при которых

X +Y < z .

48

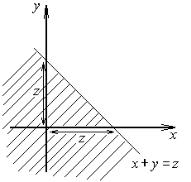
Рис. 1.16. Иллюстрация к закону распределения суммы случайных величин

Из рис. 1.16 следует:

				+∞ z−x
G(z) =	∫∫	f (x, y)dxdy =		∫		∫			(1.1.96)
							f (x, y)dy dx .
	D			−∞ −∞
Плотность распределения случайной величины Z есть
		g(z) = dG	+∞		f (x, z − x)dx .				(1.1.97)
			= ∫
		dz	−∞

Исходя из соображений симметрии, можно получить:

g(z) = dG =	+∞	f (z − y, y)dy .	(1.1.98)
	∫
dz	−∞
Таким образом, если известен		закон распределения	системы
f (x, y) , то закон распределения суммы легко получить.

Если требуется найти закон распределения независимых слу-

чайных величин, то говорят о композиции законов распределения.

Рассмотрим случай композиции двух законов распределения. Пусть имеются две случайные величины X и Y, соответственно подчиненные f1(x) и f2 ( y) . Требуется найти плотность распреде-

ления суммы этих двух независимых случайных величин. В силу независимости X и Y плотность распределения системы имеет вид f (x, y) = f1(x) f2 ( y) , тогда

+∞	+∞
g(z) = ∫	f (x, z − x)dx = ∫ f1(x) f2 (z − x)dx . (1.1.99)
−∞	−∞
	49

Операцию нахождения композиции двух законов распределения сокращенно записывают так:

g(z) = f1(x) f2 ( y) .

Композиция нормальных законов

Можно показать, что если имеется n случайных величин X1, ..., Xn , подчиненных нормальному закону, то случайная вели-

n
чина Z = ∑ Xi также подчиняется нормальному закону с парамет-
i=1
n		n
рами mz = ∑mx		и Dz = ∑Dx . Отметим тот факт, что даже если
i=1	i	i=1	i

нормально распределенные случайные величины коррелированны, то их сумма все равно распределена по нормальному закону. Только выражение для дисперсии будет иметь вид

n		+ 2∑Kx y			. Таким образом, при композиции нормаль-
Dz = ∑Dx				j
i=1	i	i< j	i

ных законов получается нормальный закон.

Нетрудно понять, что закон распределения линейной функции

						n
от нормально распределенных аргументов Z = ∑ai Xi + b также
будет нормальным с числовыми характеристиками						i=1
n			n		+ 2∑aia j Kx y
mz = ∑aimx		+ b и	Dz = ∑ai2Dx				j	. (1.1.100)
i=1	i		i=1	i	i< j	i

Предельные теоремы теории вероятностей доказывают, что при композиции большого числа любых законов закон распределения композиции близок к нормальному закону.

Предельные теоремы теории вероятностей

Предельные теоремы теории вероятностей можно условно разделить на две группы. Первая группа предельных теорем объеди-

50