12

Физически существует только один ток – переходный, и представление его в виде двух составляющих упрощает расчёт переходного процесса, сводящийся к решению линейного неоднородного дифференциального уравнения.

Частное решение такого уравнения дает принуждённый ток, общее решение однородного – свободный ток. Тогда переходный ток i = iпр +iсв есть общее

решение неоднородного дифференциального уравнения.

В нахождении принуждённой и свободной составляющих тока или напряжения (интегрировании дифференциальных уравнений) и заключается расчёт переходных процессов классическим методом.

1.4. Порядок расчёта переходного процесса

Анализ переходного процесса в разветвлённой цепи начинают с составления системы уравнений для мгновенных значений токов и напряжений, используя любой подходящий для расчётов метод (контурных токов, узловых потенциалов, законов Кирхгофа и др.). Если требуется найти какой-либо один ток i (или напряжение), то систему исходных дифференциальных уравнений путём исключения остальных переменных приводят к одному уравнению n-го порядка:

		d ni	+ a		d n −1i	+... + a di	+ a	i = u(t).	(1.8)
		dtn		n −1 dtn −1
						1 dt	0
u(t)	Принуждённая составляющая iпр зависит от вида приложенного напряжения
	– это либо постоянное, либо синусоидальное напряжение;								составляющую
iпр	находят обычными методами расчёта						установившегося		режима после

коммутации.

Физическая причина свободного процесса – несоответствие запаса электромагнитной энергии в реактивных элементах цепи в момент коммутации тому значению, которое должно быть в них после коммутации.

Свободный ток iсв представляет общее решение однородного уравнения

d ni

d n −1i

di

св

+ a

св

+... + a

св

+ a i

= 0

.

(1.9)

dtn

n −1

dtn −1

1

dt

0 св

Решение уравнения (1.9) находят в виде

i

= Аеpt .

(1.10)

св

d ki

pt

k

pt

Подставив экспоненту

Ае

и её производные

св

= Ap

e

в уравнение

(1.9), после сокращения Аеpt

dtk

получают алгебраическое уравнение степени n ,

которое называют х а р а к т е р и с т и ч е с к и м

у р а в н е н и е м:

pn + a

n−1

pn−1 +... + a p + a

0

= 0.

(1.11)

1

13

Каждый из n корней уравнения (1.11) даёт линейно независимое решение Ak e pk t ; общее решение уравнения (1.9) представляет линейную комбинацию этих решений. Вид корней pk определяет характер свободного процесса, его функциональную зависимость от времени.

Вчастном случае, если корни характеристического уравнения вещественные

иразличные, выражение свободного тока имеет вид

i		= Аep1t + A ep2t		+...+ A epnt =	n
					∑A epk t	,	(1.12)
св		1	2	n	k
где Ak – постоянные интегрирования.					k =1
Другие варианты возможных решений для iсв рассмотрены ниже							в §
1.13.	интегрирования Ak
Постоянные				в выражении	(1.12) определяют из

начальных условий – значений токов и напряжений в цепи при t = 0+ .

Прежде всего из законов коммутации (1.1) и (1.2) находят н е з а в и с и м ы е н а ч а л ь н ы е у с л о в и я (значения), которые справедливы только для тока через индуктивность и для напряжения на ёмкости. Значения

остальных токов и напряжений при t = 0+ (з а в и с и м ы е н а ч а л ь н ы е у с л о в и я) определяют по независимым начальным условиям, используя законы

Кирхгофа.

Отметим, что порядок дифференциального уравнения (1.8) (порядок цепи) равен общему числу индуктивностей и ёмкостей, для которых можно задать независимые начальные условия.

Ввиду того, что решения для свободного тока (или напряжения) в любой ветви цепи имеют стандартную форму Аеpt (1.10), а корни pk уравнения (1.11)

зависят только от параметров цепи R, L, C, нет необходимости всякий раз составлять и обрабатывать дифференциальные уравнения. Расчёт переходного процесса рекомендуется вести в следующем порядке.

1.Выбрать условно положительные направления токов в ветвях цепи.

2.Записать для искомого тока общее решение в виде i = iпр +iсв .

3.Найти iпр в установившемся режиме после коммутации.

4.Составить характеристическое уравнение и найти его корни. Его можно записать по виду дифференциального уравнения (1.9), если последнее известно. Другой, более простой способ его получения состоит в том, что для цепи находят

комплексное входное сопротивление Z вх, в котором заменяют jω на p , а затем приравнивают к нулю. Zвх( p) можно составить относительно любой ветви цепи,

причём источник ЭДС следует условно закоротить, так как его внутреннее сопротивление равно нулю.

14

5. По виду корней pk характеристического уравнения записать решение для свободного тока iсв (см. § 1.13).

6. Определить независимые начальные условия (1.1) и (1.2) iL (0− ) = iL (0+ ) и uC (0− ) = uC (0+ ) и, используя их, найти зависимые значения искомых токов (или напряжений) для t = 0+ по законам Кирхгофа.

7.Найти постоянные интегрирования.

8.Записать окончательные выражения переходных токов и напряжений.

9.Определить необходимые параметры переходного режима (постоянные времени, время переходного процесса, величину выбросов и др.).

Рассмотрим примеры расчёта переходных процессов, иллюстрирующие общие положения, изложенные выше.

1.5. Включение RL–цепи на постоянное напряжение

Известны напряжение U , параметры цепи R и L (рис. 1.5). Требуется найти

ток i и напряжения uR и uL после коммутации.
i	S t = 0	R
+
		uR
U			uL	L

-

Рис. 1.5

Для контура на рис. 1.5 составим уравнение равновесия напряжений при

t ≥ 0

R i + L di			=U	или
		dt
di	+	R i = U .		(1.13)
dt		L	L

Уравнение (1.13) – линейное неоднородное дифференциальное уравнение первого порядка имеет решение

i = iпр +iсв .

Как видно из схемы рис. 1.5, принуждённая составляющая тока iпр = UR . Её

можно найти также из уравнения (1.13), полагая в установившемся режиме dtdi = 0 .

15

Свободный ток найдём, интегрируя однородное уравнение:

diсв

+ R i

= 0.

(1.14)

dt

L св

Покажем, что результат совпадает с формулой (1.10). Разделив в уравнении

(1.14)

переменные

diсв

= −

R

dt и интегрируя полученное

равенство, найдём

i

L

diсв

R

св

∫

= −

∫dt ; ln iсв = − R t + const

или, представив const

как ln A,

i

L

L

св

icв

ln i = − R t + ln A, откуда ln

= − R t и

св

L

А

L

R

i = Аe

−

t

(1.15)

L .

св

Очевидно, что результат (1.15) совпадает с формулой (1.10) при p = − R .

Составим характеристическое уравнение

L

Zвх = R + jωL; jω = p;

Zвх( p) = R + Lp =0.

Следовательно, p = − RL , что также соответствует формуле (1.15).

+ Ae−

R

Переходной ток в цепи

i

= i

+i

= U

L t .

пр

cв

R

Найдём постоянную

интегрирования

A. На основании первого

коммутации, для цепи на рис. 1.5 i(0− ) = i(0+ ) = 0.

Для момента t = 0+

R

i(0+) = 0 = U + Ae−

0

, откуда A = −U

L

, и окончательно

R

R

R

U

U

−

t

i =

−

R

R

e

L

;

R

−

t

L

u

R

= Ri =U −Ue

;

R

−

t

u

L

=U −u

R

=Ue

L

,

или непосредственно через i

закона

(1.16)

(1.17)

16

= L(−U )(− R)e−

R

R

u

L

= L di

L t =Ue−

L t .

(1.18)

dt

R

L

Кроме того, найдём закон изменения индуктивного сопротивления X L (t)

после коммутации

R

u

Ue−

t

R

X L (t) =

L

=

L

=

i

U

−

R

t

R

t

.

(1.19)

(1 − e

L

)

e L

−1

R

iсв, i , uR , uL ,

X L (t) во время

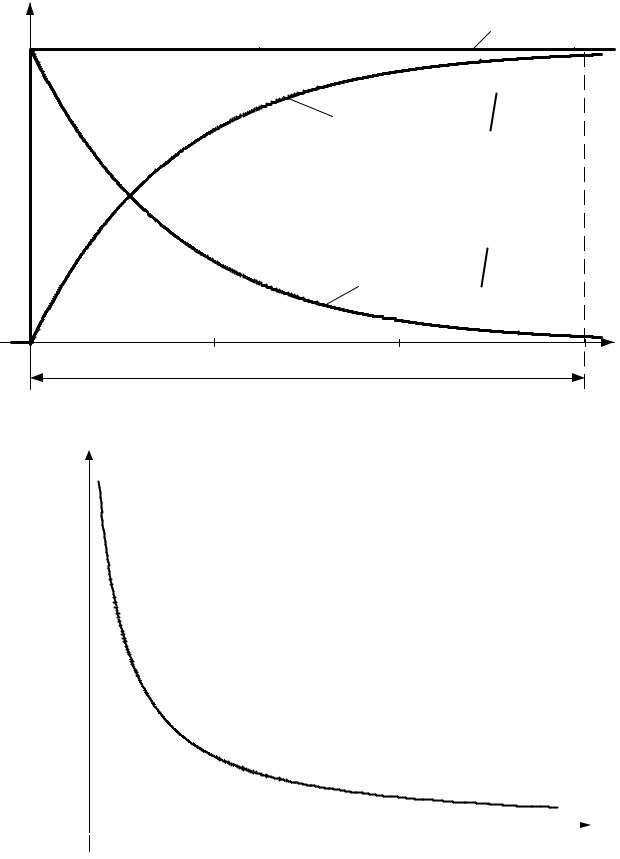
На рис. 1.6 а-в приведены кривые изменения

переходного процесса.

X L (t) при t = 0 принимает бесконечно большое

Обратим внимание, что

значение (“обрыв” цепи на индуктивности), а uL

изменяется скачком от 0 до U

(рис. 1.6 б).

i	t пп =	3 τ	iпр =	U
				R
U
R
	i =	U (	−t τ)
		R 1− e
0	τ = L		2τ	3τ	t
	R
	i св= −U e−t τ
	R
−U
R		а

	17
uR	uL			uR пр =U
U
	u	=U	)	1− e−ττ)
	R
		uL = Ue−τ τ
	τ = L
0	R	2τ		3τ t
	tпп = 3 τ
	б
X L (t)

0	τ		2	τ	3	τ t

в

Рис. 1.6

18

1.6. Экспонента. Постоянная времени цепи. Время переходного процесса

В цепях первого порядка характеристическое уравнение имеет один вещественный отрицательный корень p1, а изменение свободного тока (или напряжения) подчиняется экспоненциальному закону

i

= Ae p1t = Ae−t /τ = Ae−β t .

(1.20)

св

1

В формуле (1.20) величина τ

=

называется постоянной времени цепи.

p

A

1

При

t =τ значение

i

=

, т.е.

постоянная времени τ

равна промежутку

св

е

времени, в течение которого свободный ток уменьшается в е=2,718 раза.

Величина β = 1 называется коэффициентом затухания цепи и, подобно							p ,
τ							1
имеет размерность c−1. Значения p , τ ,			β зависят от схемы и её параметров.
	1
Свободный ток затухает тем медленнее, чем больше постоянная времени τ							(чем
меньше коэффициент затухания β ).		], β	= R [c−1 ],			[c ]. При любом t
Для цепи (рис. 1.5) p = − R [c−1				τ =	L
1	L		L		R

показатель экспоненты в формуле (1.20) – всегда безразмерное число.

Задавая значения t кратными τ , рассчитаем координаты характерных точек

−t

экспоненты e τ (табл. 1.1) и построим её график (рис. 1.7).

							Таблица 1.1
t	t=0	t=τ	t=2τ	t=3τ	t=4τ	t=4,6τ	t=5τ
e-t/τ	e0=1,0	e-1=0,368	e-2=0,135	e-3=0,05	e-4=0,018	e-4,6=0,01	e-5=0,007

19

e−t τ

1

0,75

0,5

0,368

0,25

0,135

0, 05

0,018

0,007

0

τ

2

τ

3

τ

4

τ

τ

t

5

Рис.1.7

− t1

Проведём касательную к экспоненте в произвольной точке B (t , e

τ

) рис.

1.8.

1

−t1

e

tgα = −tg(180

o

−α) = −m

τ

,

(1.21)

x

где x – длина подкасательной; m – масштабный коэффициент для

выравнивания масштабов по осям при вычислении tgα ; m припишем

экспоненте.

e−t τ

e −t τ

1

1

−

τ A

B

e−t1

τ A

B

e t1

1

=0, 368

t1

α

e

t

t

0

D

x

C

0

τ

Рис. 1.8

Рис. 1.9

20

−

t

−

t

me

Так как

tgα =

d(me

τ )

= −

τ

то с учётом выражения

(1.21)

dt

τ

,

получим для t = t1

t1

t1

−

−

−

me

τ

= −

me

τ

(1.22)

x

τ

,

откуда следует, что x =τ , т.е. длина подкасательной в любой точке экспоненты численно равна τ.

Это обстоятельство указывает на способ определения постоянной времени τ по экспериментально полученной экспоненте.

Точность нахождения τ будет выше, если касательную к экспоненте

построить при t = 0 (рис. 1.7), так как при малых t

экспонента аппроксимируется

прямой. Действительно, разложение экспоненты в степенной ряд [13]

−

t

t

t

2

3

e τ =1−

t

+

/ 2!−

/ 3!+...

(1.23)

τ

τ

τ

− t

τ ≈1− t

с погрешностью

менее

уже t ≤ 0,2τ даёт линейную функцию e

2%.

τ

Другой способ определения τ по экспоненте показан на рис. 1.9.

На уровне 0,368 от начального значения экспоненты проводим прямую АВ параллельно оси t . Отрезок АВ равен τ .

Время переходного процесса (tnn ) – наименьшее время, отсчитываемое от

момента коммутации до момента, после которого отклонение переходного тока (напряжения) от установившегося значения не превышает заданной малой величины. На практике, как правило, переходный процесс считают закончившимся по прошествии времени равного 3τ; к этому моменту свободные составляющие уменьшаются до уровня 0,05 от начального значения, а переходные токи и напряжения отклоняются на 0,05 от принуждённых значений (табл.1.1, рис. 1.6 а, б).