25
∞
∫ f (t)δ(t −to)dt = f (to),	(3.5)
−∞
где δ(t −to) - единичная импульсная функция, смещённая на время t0	(рис. 3.1
в).

Выражения (3.4) и (3.5) описывают фильтрующее (стробирующее) свойство функции δ(t).

Единичная ступенчатая и единичная импульсная функции относятся к семейству разрывных или особых функций и используются для идеализированного представления сигналов.

Эти сигналы, часто называемые в теории цепей единичный скачок напряжения и единичный импульс, обычно выбираются в качестве типового внешнего воздействия (возмущения), приложенного ко входу цепи (системы), при котором переходный процесс носит наиболее неблагоприятный характер. Кроме того, при помощи интеграла Дюамеля и интеграла свёртки они позволяют вычислить реакцию цепи на любое внешнее возмущение.

3.2. Переходные функции цепи. Импульсная переходная функция

Переходной функцией называют реакцию цепи на воздействие единичного скачка напряжения (или тока).

Под реакцией понимают изменение во времени напряжения на любом участке цепи или тока в любой её ветви. Переходную функцию цепи определяют при нулевых начальных условиях.

При воздействии на входе цепи скачка напряжения U ток i(t)в любой ветви

можно представить в виде произведения напряжения U на проводимость у(t)

i(t) =U у(t),

а напряжение на каком-либо участке цепи

u(t) =U h(t).

Для единичного скачка напряжения, т.е. при U =1B
i1(t) = 1 у(t),	(3.6)
где у(t)[См]- так называемая переходная проводимость;
u1(t) =1 h(t) = h(t),	(3.7)

h(t) - переходная функция по напряжению - это безразмерная величина,

численно равная напряжению на каком-либо участке цепи, если на вход цепи подать постоянное напряжение в 1В.

Переходные функции цепи у(t) и h(t) , называемые также переходными характеристиками, можно найти классическим или операторным методом.

26

Пример 3.1

При включении последовательной RL-цепи на постоянное напряжение

U (рис. 1.5) ток и напряжение на резисторе и индуктивной катушке равны (1.16), (1.17), (1.18):

		R			R			R
i = U	(1−e−		t );	uR =U (1−e−		t );	uL =Ue−		t .
								L
					L
		L
R

Полагая в этих формулах U =1B , получим переходную проводимость и переходные функции для напряжений

R

R

R

1

(1−e−

t )[См];

−

t ;

hL (t) = e−

t .

L

hR (t) =1−e

L

у(t) =

L

R

Пример 3.2

Найдём переходные функции последовательной RC-цепи (рис. 1.13), в

которой (1.29), (1.30), (1.31):

t

U

−

t

−

−

t

uR =Ue

RC ;

RC ).

i =

e

RC ;

uC (t) =U (1−e

R

При U =1B найдём

1

−

t

−

t

−

t

RC [Cм];

RC

у(t) =

e

h

R

(t) = e

; h (t) =1−e

RC .

R

C

Импульсной переходной функцией k(t) * называется реакция цепи на воздействие единичной импульсной функции δ(t).

Поскольку внешние воздействия 1(t) и δ(t)связаны формулой (3.2)

	δ(t) =	d1(t)	, то аналогичной зависимостью связаны и их реакции					h(t) и k(t)
		dt
	(так как цепь линейная):
			k(t) =	dh(t)	при h(0+ ) = 0.			(3.8)
				dt
	Если h(0+ ) ≠ 0, то					dh(t)
			k(t) = h(0+ )δ(t) +				.	(3.9)
						dt

27

Пример 3.3

Например, при включении RL-цепи

на

единичный скачок

напряжения

R

переходная

функция

hL (t) = e− L t

и

h(0+ ) =1,

импульсная

переходная

функция kL

R

−Rt

(t) =δ(t) −

L

e

L .

Для RC-цепи h (t) =1−e− t RC ,

h (0

+

) = 0;

k

C

(t) =

1

e− t RC .

C

C

RC

Для нахождения функций h(t) и k(t) операторным методом их

изображения выражают через передаточную функцию четырёхполюсника K ( p) :

h(t)

K ( p)

; k(t) K ( p).

p

__________________________________________________________________

* Другие названия импульсной переходной функции: импульсная переходная характеристика,

импульсная характеристика, импульсная реакция, отклик, весовая функция и обозначения:

g(t) , h(t) , hu (t) , hδ (t) , w(t) ,

h′(t) .

Переходная функция h(t)и импульсная переходная

функция k(t) являются

основными характеристиками цепи (звена, системы) в вещественной области и

полностью определяют её динамические свойства (поведение в переходном

режиме).

3.3. Расчёт переходных процессов с помощью интеграла Дюамеля

u(τ)

′

∆u ≈ u (τ)∆τ

∆τ

S t = 0 i(t)

u(t)

П

u(0)

t

τ

0

τ

t −τ

а

Рис. 3.2

б

28

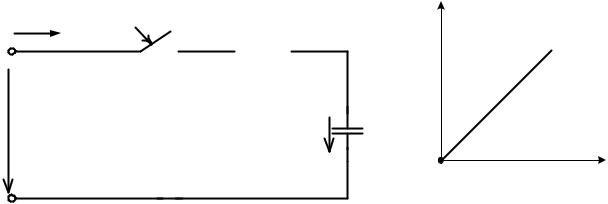
Пассивный двухполюсник (рис. 3.2 а) включается на непрерывно

изменяющееся напряжение u(t) (рис. 3.2 б). Требуется найти ток i(t) в

произвольной ветви двухполюсника после замыкания ключа.

Введём переменную τ , по которой будем вычислять интеграл Дюамеля, а через t обозначим некоторый (текущий) момент времени, в который будем определять ток i(t).

Заменим непрерывную кривую u(τ) ступенчатой функцией и просуммируем составляющие искомого тока, вызванные начальным скачком напряжения u(0) и всеми последующими скачками ∆u , сдвинутыми на время ∆τ друг относительно друга.

Напряжение u(0) вызовет ток u(0) у(t), где у(t) - переходная проводимость, определённая для ветви, в которой вычисляется i(t).

Элементарный скачок напряжения∆u (рис. 3.2 б) может быть выражен через производную

∆u ≈ ∆τ dduτ = ∆τ u′(τ);

ток, вызванный скачком ∆u в момент времени τ , равен

∆u у(t −τ) = u′(τ) у(t −τ)∆τ.

Суммируя составляющие тока от всех скачков на интервале времени τ = 0 до
τ = t и переходя от суммы к интегралу при ∆τ → 0, получим выражение
t
i(t) = u(0) у(t) + ∫u′(τ) у(t −τ)dτ.	(3.10)
0

Эта формула называется интегралом Дюамеля. С её помощью можно найти также и напряжение, если вместо у(t) использовать h(t).

Если теперь провести замену переменной в подынтегральной функции (3.10):

t −τ = x; τ =t − x; dτ = −dx; u (τ) = u (t − x)

′

′

0

t

∫u′(t − x) у(x)(−dx)

= ∫u′(t − x) у(x)dx и вновь заменить x

на τ , то

t

0

получим вторую форму интеграла Дюамеля

t

i(t) = u(0) у(t) +

∫u′(t −τ) у(τ)dτ.

(3.11)

0

∫w dv = wv − ∫v dw,

Интегрируя по частям выражение (3.10)

обозначив

при этом w

=

у(t

−τ

);

dw

= −

′

−τ

)d

τ

;

′

v =u(τ),

у (t

dv = u (τ)dτ;

получим третью форму интеграла Дюамеля

					29
i(t) = u(0)у(t) + ∫t		u′(τ)у(t −τ)dτ =
	0
				t	t	′
= u(0) у(t) + у(t −τ)u(τ)				0 −	∫u(τ)[−у (t −τ)]dτ =
					0
= u(0) у(t) + у(0)u(t) −u(0) у(t) + ∫t						u(τ) у′(t −τ)dτ =
					0
= у(0)u(t) + ∫t	u(τ) у′(t −τ)dτ .						(3.12)
0
Наконец, интегрируя по частям формулу (3.11), найдём четвёртую форму
интеграла Дюамеля					t
						′	(3.13)
	i(t) = у(0)u(t) + ∫u(t −τ) у (τ)dτ.
					0

При расчетах рекомендуется выбрать из формул (3.10) – (3.13) ту, которая даёт наиболее простое подынтегральное выражение. К примеру, в заданиях на

курсовую работу [12], в которых внешнее воздействие u(t) задано в виде

отрезков прямых, целесообразно использовать выражение (3.10), так как производная от линейной функции даёт постоянное число.

Пример 3.4

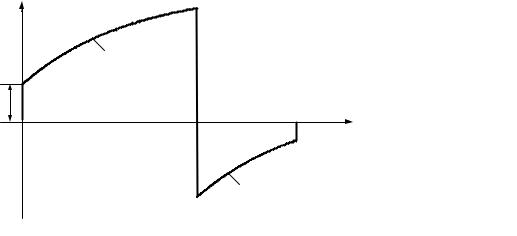
Напряжение в цепи (рис. 3.3 а) изменяется по линейному закону u(t) = at, u(0) = 0 (рис. 3.3 б).

Найти законы изменения тока в цепи и напряжение uC (t).

i(t)	t=0				u(t)
	S		R

u(t)	C
	uC (t)

0

t

а

б

Рис. 3.3

	30
i(t)	iпр= aC
aC
	i(t) =aC(1 −e−t/RC )
0	t
i	=−aCe−t/RC
cв
− aC
	в
Продолжение рис. 3.3

Выбираем формулу (3.10), в которой u(τ) = aτ;	1			− t	RC
	у(t) =		e
		R
(пример3.2);

1

−

t−τ

у(t −τ) =

e

RC ;

R

t

i(t) = u(0) у(t) + ∫u′(τ) у(t

a

−t

0

τ

t

=

e

RC RCе

RC

0

R

− t

h (t −τ) =1−e

−

t −τ

h (t) =1−e

RC ;

RC .

c

c

t

1

−

t−τ

a

−t

t

τ

−τ)dτ = 0 + ∫a

e

RC dτ =

e

RC ∫e

RC dτ =

R

R

0

0

= aCe−t RC (e t RC −1) = aC(1 − e−t RC ). (3.14)

	t	−	t −τ				t
	uC (t) = 0 + ∫a(1 − e			)dτ = aτ		t0 − ae−t RC ∫eτ RC dτ =
			RC
	0						0
				= at −aRC(1−e−t RC ).				(3.15)
	График тока i(t) приведён на рис. 3.3 в,						uC (t)	- на рис. 3.9.

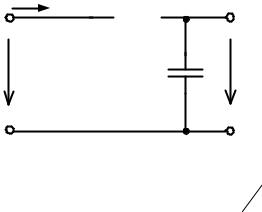
Рассмотрим применение интеграла Дюамеля при сложной форме напряжения u(t) на входе пассивного двухполюсника (рис. 3.2 а). Напряжение u(t) задано в

виде кусочно-непрерывной функции (рис. 3.4).

Требуется найти ток в одной из ветвей двухполюсника; переходная проводимость ветви у(t) известна.

i(t).

		31
u(t)	a ua
	u1(t)
u(0)	t1	t2
0		c uc	t
	uвв	u2(t)

Рис. 3.4

При заданном внешнем воздействии (рис. 3.4) переходный процесс с помощью интеграла Дюамеля рассчитывают для трёх интервалов времени.

Для первого интервала времени 0 ≤ t < t1

t

i(t) = u(0) у(t) + ∫u1′(t) у(t −τ)dτ,

0

где u1 (t) - закон изменения u(t) в первом интервале без учёта скачка при t = t1 . Для второго интервала времени t1 ≤ t < t2

t	t
i(t) = u(0) у(t) + ∫1 u1′(τ) у(t −τ)dτ + (uв −ua ) у(t −t1) + ∫u2′ (τ) у(t −τ)dτ,
0	t1
где u2 (t) - закон изменения u(t)	во втором интервале, слагаемое

(uв −ua )у(t −t1) учитывает скачок напряжения (со знаком “минус”) в момент

времени t1 .

Для третьего интервала времени t2 ≤ t < ∞

t	t
i(t) = u(0) у(t) + ∫1 u1′(τ) у(t −τ)dτ + (uв −ua ) у(t −t1) + ∫2 u2′(τ) у(t −τ)dτ +
0	t1

+(0 −uC ) у(t −t2 ),

слагаемое (0 −uC ) у(t −t2 ) учитывает положительный скачок напряжения в момент времени t2 .

Пример 3.5

На входе цепи (рис. 3.5) действует прямоугольный импульс (рис. 3.6 а). Найти напряжение на ёмкости uC (t) и ток в цепи

32

i(t) R

u(t)		C		uC (t)

Рис. 3.5

Переходная функция по напряжению hC (t) =1−e−t RC (пример 3.2):

	−	1	(t−τ)
		RC		u(0) =U; u (τ) = 0.
	hC (t −τ) =1−e		;
				′

В первом интервале времени, 0 ≤ t < tu , заменив в формуле (3.10) у(t) на hC (t) , найдём

						t
	uC1(t) = u(0)hC (t) + ∫u′(τ
			0
		duC	1
				U	e−		t .
	i (t) = C		=			RC
	1	dt		R

Во втором интервале времени,

	−	1	t
		RC
	)h (t −τ)dτ =U (1−e		) +0.
	C

tu ≤ t < ∞ найдём

t

uC2 (t) = u(0)hC (t) + ∫u u′(τ)hC (t −τ)dτ −UhC (t −tu ) =

1

0

1

−

t

−

(t −tu )

RC

=U (1−e

)

+0 −U[1−e

RC

] =

1

t

1

t e

tu

tu

1

t .

=U −Ue−

−U +Ue−

=U (e

−1)e−

RC

RC

RC

RC

RC

duC2

U

tu

−1)e−

1

t .

i2 (t) = C

= −

(e RC

RC

R

tu

dt

U

−

i

(t

) −i

(t

U

i

2

(t

u

) =

(e RC −1);

2

u

u

) = −

.

R

1

R

На рис. 3.6 б и в, качественно построены кривые uC (t) и i(t).

						33
		u(t)
			U
a uc				0		tи	t
			(t)		τ
		t		U
	-
		и
U(1−e		RC)				uc2	(t )
б				0	uc1 (t)
					tи		t
	i (t)
			U
				R	i1 (t)
U	−		tи
R	e		RC			U
						R
в				0	tи		t
−	tи					i2 (t)
U(e RC−1)
R
					Рис.3.6

34

3.4. Расчёт переходных процессов с использованием импульсной переходной функции

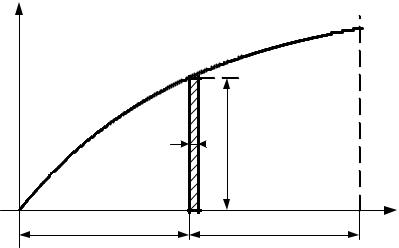
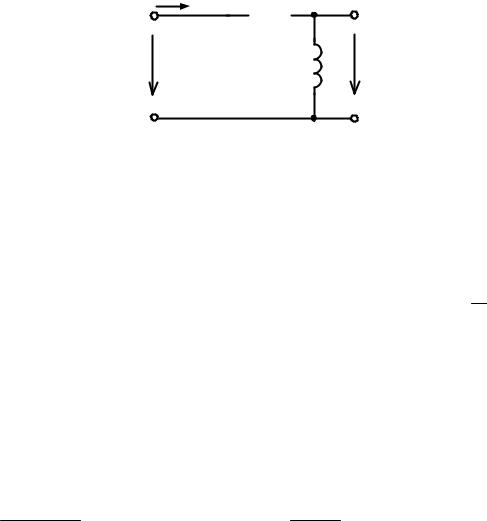
Пусть к входу пассивного двухполюсника (рис. 3.2 а) приложено внешнее воздействие в виде непрерывной функции u(t) (рис. 3.7). Найдём реакцию на выходе цепи (напряжение, к примеру, на одном из элементов), если известна импульсная переходная функция цепи k(t).

Представим кривую u(τ) в виде последовательности примыкающих друг к другу прямоугольных импульсов с длительностью ∆τ и амплитудой u(τ) для моментов времени τ . Для единичного импульса δ(τ) составляющая реакций в момент времени t равна импульсной переходной функции k(t −τ).

u(τ)
		∆τ u(τ)
	τ	t −τ	t
0			τ
		Рис. 3.7

Но площадь рассматриваемого импульса не	равна единице, а равна
u(τ)∆τ , поэтому реакция на него в момент времени t	будет k(t −τ)u(τ)∆τ .
Суммируя составляющие реакции от действия всех импульсов, каждый из

которых имеет бесконечно малую длительность ( ∆τ → 0 ) от τ = 0 до τ = t , получим полную реакцию на выходе цепи

t
uвых(t) = ∫u(τ)k(t −τ)dτ.	(3.16)
0

Формула (3.16) называется с в ё р т к о й двух функций u(t) и k(t).

Заменив переменную в подынтегральном выражении (3.16) , получим вторую форму интеграла свёртки

t
uвых(t) = ∫k(τ)u(t −τ)dτ.	(3.17)
0

35

С помощью формул свёртки (3.16) и (3.17) можно определить реакцию цепи на внешнее воздействие и в том случае, если оно имеет вид кусочно-непрерывной функции (например, рис. 3.4).

Формулы свёртки (3.16) и (3.17) являются разновидностью интегралов Дюамеля (3.10) – (3.13).

Интегралы Дюамеля и свёртки называют также интегралами н а л о ж е н и я, что отражает возможность их использования для расчёта переходных процессов только в линейных электрических цепях.

Пример 3.6

На входе цепи (рис. 3.8) действует экспоненциальное напряжение

	−α t	при t	≥ 0,
Ue
u(t) =	при t < 0.
0
			i(t)		R
		u(t)					L uL(t)

Рис. 3.8

Найти напряжение на индуктивности

R

−

R

t

kL (t) = δ(t) −

e

L

;

L

R

R

−

(t−τ)

kL (t −τ) = δ(t −τ) −

e

L

= δ(t

L

Используя выражение (3.16), найдём

uL (t).

−τ) − βe−β(t−τ) , где β = RL .

uL (t) :

t	t
uL (t) = ∫u(τ)kL (t −τ)dτ = ∫Ue−ατ [δ(t −τ) − βe−β(t −τ) ]dτ =
0	0

t

=U ∫e−ατδ(t −τ)dτ

0

=Ue−α t − βUe−β t

−(α − β)

t

− βUe−β t ∫e−(α−β)τ dτ =

0

[e−(α−β)t −1] =Ue−α t +αβ−Uβ (e−α t −e−β t ) =

36

=

αU

e

−α t

−

βU

e

−β t

.

(3.18)

α − β

α − β

Пример 3.7

а) приложено внешнее воздействие u(t) = at, u(0) =0

К цепи (рис. 3.3

(рис. 3.3 б). Найти напряжение uC на ёмкости и ток в цепи.

Для получения uC используем импульсную переходную функцию (пример

3.3):

t −τ

1

− t

1

−

′

RC

RC

u(τ) = aτ.

kC (t) = hC (t) =

RC

e

;

kC (t −τ) =

RC

e

;

Подставляя u(τ) и kC (t −τ) в формулу (3.16) и интегрируя по частям, найдём uC (t) :

= t u(τ)k

(t −τ)dτ = t aτ

1

e−

t −τ

a

e− t RC t

τeτ

u

(t)

C

RC

dτ =

RCdτ =

C

∫

∫

RC

RC

∫

0

t

0

0

a

e− t RC (τRCeτ RC

=

t0 − ∫RCeτ RC dτ) =

RC

0

=

a

e− t RC [RCte t RC

−(RC)2 e t RC +(RC)2 ] =

RC

− t

− t

= at −aRC +aRCe

RC = at −aRC(1−e

RC ).

(3.19)

i(t) = C

duC

= aC − aCe− t RC = aC(1− e− t RC ).

(3.20)

dt

− t

uR (t) = Ri(t) = aRC(1−e

RC ).

(3.21)

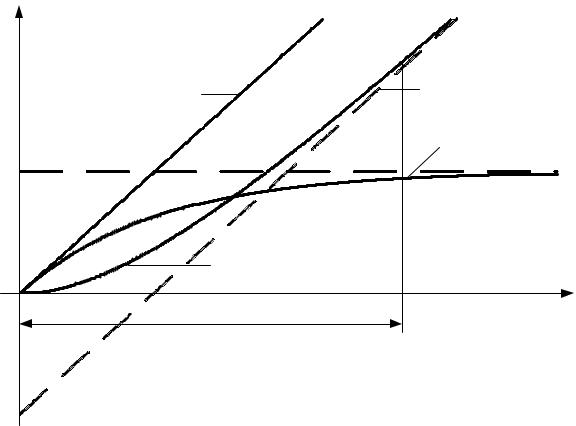
Результаты выражений (3.19) и (3.20) совпадают с выражениями (3.15) и (3.14), полученными с использованием интеграла Дюамеля. Графики

u(t),uC (t),uR (t) показаны на рис. 3.9.

		37
u (t )
uC (t)
uR (t)
u(t) = at				uC пр= at − aRC
			uR(t ) = aRC (1−e−t/ RC)
aRC
u	C	(t) = at − aRC (1	−e−t/	RC )
0
				t
tПП=	3 RC
- aRC
		Рис. 3.9