Prak_Geom1

V = ½(l1; l2) ¢ SM1Q1P1N1

7±: Довести, що вiдстань мiж двома мимобiжними прямими l1 i l2 може бути знайдена

за формулою	; l2) = j¡¡¡¡!	j;	(2.74)
½(l1
	M1M2p~1p~2

j[p~1; p~2]j

äå M1 i p~1 точка i напрямний вектор прямо¨ l1, à M2 i p~2 точка i напрямний вектор прямо¨ l2.

Розглянемо площину ¾1, яка проходить через пряму l1 паралельно до прямо¨ l2, i площину ¾2, що проходить через пряму l2 паралельно до l1. Вiдомо, що такi площини iснують i визначаються однозначно. Ясно, що ½(l1; l2) дорiвню¹ вiдстанi мiж паралельними площинами ¾1 i ¾2. Для знаходження цi¹¨ вiдстанi побуду¹мо паралелепiпед M1N1P1Q1M2N2P2Q2 òàê, ÿê показано на рисунку на сторiнцi 121, i позначимо через V об'¹м цього паралелепiпеда.

Âiäîìî, ùî îá'¹ì V			даного паралелепiпеда		дорiвню¹ абсолютнiй величинi мiшаного
добутку векторiв	¡¡¡¡!	, p~1 i p~2, тобто V =		j¡¡¡¡!		j	.
	M1M2			M1M2p~1p~2

З iншого боку,

= ½(l1; l2) ¢ j[p~1; p~2]j:

¡¡¡¡!

Таким чином, jM1M2p~1p~2j = ½(l1; l2) ¢ j[p~1; p~2]j. Звiдси отриму¹мо формулу (2.74).

121

2.3 Перетворення простору

1 Рух простору

Рух простору. Приклади рухiв в просторi. Поняття про репер в просторi. Основна теорема про рух в просторi.

Кажуть, що перетворення простору зберiга¹ вiдстань0 , ÿêùî0 вiдстань мiж0 0довiльними. точками A i B простору рiвна вiдстанi мiж ¨х образами A i B , тобто AB = A B

Означення 2.5. Перетворення простору, яке зберiга¹ вiдстань, назива¹ться рухом (або

перемiщенням).

Приклад 1. Нехай p~ довiльний

вектор простору. Кожнiй точцi M поставим у

вiдповiднiсть точку

M0

¡¡¡!

=

p~. Òàêå

перетворення простору назива¹ться

òàê, ùîá MM0

паралельним перенесенням на вектор p~.

Доведемо, що таке перетворення ¹ рухом. Справдi, нехай M1 i M2 довiльнi точки, а M10

M0 ¨х образи. Тодi

¡¡¡¡1 !

=

¡¡¡¡2 !

=

¡¡¡¡1 ! =

¡¡¡¡2 !. За лемою 1.1 про рiвнiсть

i

2

M M0

p~ i M M0

p~, òîìó M M0

M M0

1

2

1

2

M1M2 =

¡¡¡¡!, òîìó

1 2 =

0

0.

векторiв отриму¹мо ¡¡¡¡!

1

2

M M

1

M

2

M0

M0

M

Приклад 2. Задамо в просторi точку O i розглянемо вiдображення простору, при якому кожна точка M переходить в точку M0, симетричну точцi M вiдносно точки O.

Таке вiдображення ¹ перетворенням простору i назива¹ться симетрi¹ю вiдносно точки O або центральною симетрi¹ю. Неважко бачити, що це перетворення ¹ рухом.

Приклад 3. Задамо в просторi площину ¾ i розглянемо вiдображення простору, при якому кожна точка M переходить в точку M0, симетричну точцi M вiдносно площини ¾.

Таке вiдображення ¹ перетворенням простору i назива¹ться симетрi¹ю вiдносно площини. Доведемо, що симетрiя вiдносно площини ¹ рух. Для цього виберемо прямокутну систему координат таким чином, щоб дана площина спiвпадала з координатною площиною Oxy.

Нехай A(x1; y1; z1) i B(x2; y2; z2) довiльнi двi точки простору, а A0 i B0 ¨х образи. Очевидно, точки A0 i B0 матимуть координати A0(x1; y1; ¡z1) i B0(x2; y2; ¡z2). За формулою (2.4) вiдстанi

мiж двома точками простору знаходимо:

p

AB = (x2 ¡ x1)2 + (y2 ¡ y1)2 + (z2 ¡ z1)2; A0B0 = p(x2 ¡ x1)2 + (y2 ¡ y1)2 + (z2 ¡ z1)2;

òîìó AB = A0B0. Отже симетрiя вiдносно площини ¹ рух.

Впорядкована четвiрка точок A, B, C, D простору, якi не лежать в однiй площинi назива¹ться репером i познача¹ться так: R = (A; B; C; D). Точки A, B, C i D називаються вершинами репера, причому точка A назива¹ться його початком. Репер назива¹ться афiнним, якщо тетраедр ABCD довiльний, i ортонормованим, якщо ребра AB, AC, AD цього тетраедра вза¹мно перпендикулярнi i AB = AC = AD = 1.

äå	Як i для площини кожнiй системi координат O~e1~e2~e3 вiдповiда¹ репер R = (O; E1; E2; E3),
	¡¡!	¡¡!	¡¡!	= ~e3. Будемо казати, що точка M в реперi R ма¹ координати
	OE1	= ~e1, OE2	= ~e2, OE3

(x; y; z), ÿêùî (x; y; z) координати точки M у вiдповiднiй системi координат.

Ëåìà 2.5. ßêùî R = (A; B; C; D) i R 0 = (A0; B0; C0; D0) довiльнi афiннi репери, то iсну¹ не бiльш одного руху, який репер R переводить в репер R 0.

122

Доведення. Припустимо, що ¹ два рухи g1 i g2, якi переводять репер R в репер R 0, причому

g1 =6 g2. Це означа¹, що знайдеться така точка M, ùî ì๠ìiñöå íåðiâíiñòü g1(M) =6 g2(M). Нехай g1(M) = M1 i g2(M) = M2. Îòæå, M1 6= M2. Îñêiëüêè g1(A) = A0 i g2(A) = A0, òî AM = A0M1 (вiдносно g1) i AM = A0M2 (вiдносно g2), òîìó A0M1 = A0M2, звiдки виплива¹, що точка A0 рiвновiддалена вiд точок M1, M2. Аналогiчно показу¹мо, що точки B0, C0, D0 також рiвновiддаленi вiд точок M1, M2. Таким чином, точки A0; B0; C0; D0 лежать в площинi, яка

перпендикулярна до вiдрiзка M1M2 i проходить через його середину. Це протирiччить тому, що данi точки утворюють репер. Отже, наше припущення g1 6= g2 íåâiðíå, òîìó g1 = g2.

Теорема 2.11 (основна теорема руху). Нехай R = (A; B; C; D) i R 0 = (A0; B 0; C 0; D 0)

довiльнi ортонормованi репери. Тодi iсну¹ один i тiльки один рух, який репер R переводить

âрепер R 0. При цьому русi довiльна точка M з даними координатами в реперi R переходить

âточку M0 з тими ж самими координатами в реперi R 0.

Доведення. Розглянемо перетворення простору g: M 7!M0, при якому точка M в реперi R i

точка M0 в реперi R 0	мають однаковi координати (x; y; z). Доведемо, що це перетворення
буде рухом. Справдi,	нехай g: M1(x1; y1; z1)R		7!	M10(x1; y1; z1)R 0 i g: M2(x2; y2; z2)R	7!
M20(x2; y2; z2)R 0, äå M1; M2; M10; M20		точки простору. Знайдемо вiдстанi M1M2 i M10M20			çà
формулою (2.4):

M1M2 = p(x2 ¡ x1)2 + (y2 ¡ y1)2 + (z2 ¡ z1)2; M10M20 = p(x2 ¡ x1)2 + (y2 ¡ y1)2 + (z2 ¡ z1)2;

звiдки виплива¹ M1M2 = M10M20. Îòæå, g рух. Згiдно леми 2.5 цей рух ¹диний.

Виходячи з теореми 2.11, як це було зроблено для випадку площини (див. стор. 42 44), можна довести такi властивостi руху простору:

1±:

2±:

3±:

4±:

5±:

6±:

Рух простору переводить площину в площину, а паралельнi площини у паралельнi площини.

Рух простору переводить пряму у пряму, а паралельнi прямi у паралельнi прямi.

Рух простору переводить напiвплощину у напiвплощину, напiвпростiр у напiвпростiр.

Рух простору переводить двогранний кут в рiвний йому двогранний кут. Рух зберiга¹ перпендикулярнiсть площин i прямих у просторi.

Рух простору зберiга¹ просте вiдношення трьох точок прямо¨, зберiга¹ вiдношення "лежати мiж".

Рух простору переводить ортонормований репер в ортонормований репер.

2 Два види руху. Iнварiантнi точки прямi та площини

Орi¹нтовнiсть реперiв у просторi. Iнварiантнi точки прямi та площини. Iндукований рух. Лема про рух, який нема¹ iнварiантних точок. Лема про iснування iнварiантно¨ прямо¨.

Говорять, що репери R = (O; A; B; C) i R 0 =	(O0; A0; B0; C0) орi¹нтованi однаково
OA; OB; OC	¡¡! ¡¡! ¡¡!
(протилежно орi¹нтованi), якщо базиси ¡! ¡¡! ¡!	i O0A0; O0B0; O0C0 орi¹нтованi однаково

123

паралельнi

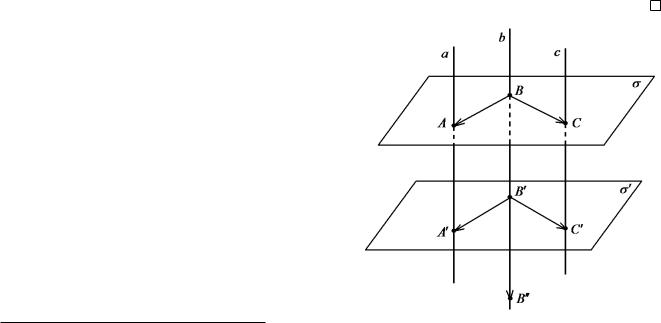
(протилежно). Таким чином, репери			R i R 0		однаково орi¹нтованi, якщо RjR 0				> 0, i
	R R	< 0		R	R	0	= (OA; OB; OC)	(¡¡! ¡¡! ¡¡!)
протилежно орi¹нтованi якщо	j 0		. Òóò	j			¡! ¡¡! ¡! j	O0A0; O0B0; O0C	0 :

Можна довести, що рух простору або зберiга¹ орi¹нтацiю простору, або змiню¹ орi¹нтацiю на протилежну.7 Отже, в просторi, як i на площинi, iсну¹ два види руху: однi зберiгають орi¹нтацiю простору, а iншi змiнюють на протилежну. В першому випадку рухи називаються рухами першого роду, а в другому рухами другого роду.

Як i у випадку площини точку простору ми назива¹мо iнварiантною (або нерухомою) точкою перетворення, якщо вона переходить сама в себе. Аналогiчно пряму (площину) назвемо iнварiантною (або нерухомою), якщо ¨¨ образ спiвпада¹ з нею. Частинним випадком iнварiантно¨ прямо¨ (площини) ¹ пряма (площина) iнварiантних точок, всi точки яко¨ ¹ iнварiантними.

Нехай g даний рух простору, а ¾ iнварiантна площина. Це означа¹, що довiльна точка площини ¾ переходить в точку цi¹¨ ж площини, тобто на площинi ¾ встановлю¹ться деяке вiдображення g 0, яке, очевидно, ¹ перетворенням. А оскiльки g зберiга¹ вiдстань, то i g 0 íà площинi ¾ також зберiга¹ вiдстань, тобто g 0 рух площини ¾. Надалi будемо казати, що вiн iндукований рухом g на площинi ¾.

Ëåìà 2.6. Якщо рух у просторi нема¹ iнварiантних точок, то довiльнi двi його iнварiантнi прямi паралельнi.

Доведення. Припустимо, що iснують двi непаралельнi iнварiантнi прямi p i q ïðè ðóñi g. В просторi логiчно можливi два випадки: а) p i q перетинаються, б) p i q мимобiжнi.

а) Нехай прямi p i q перетинаються в точцi M. Оскiльки цi прямi ¹ iнварiантними, то очевидно точка M при русi перейде сама в себе, тобто вона ¹ нерухомою. А це протирiччить

óìîâi ëåìè.

б) Позначимо через AB спiльний перпендикуляр до прямих p i q. Оскiльки при русi вiдстань мiж точками зберiга¹ться i враховуючи, що довжина перпендикуляра AB ¹ найкоротшою вiдстанню мiж даними прямими, то очевидно при русi перпендикуляр AB перейде сам в себе, звiдки виплива¹, що A 7!A i B 7!B, тобто точки A i B ¹ iнварiантними,

що неможливо згiдно умови.

Таким чином, прямi p i q паралельнi.

Ëåìà 2.7. ßêùî ðóõ g íåì๠iíâàðiàíò-

них точок, але ма¹ принаймнi три попарно паралельнi iнварiантнi прямi, що не лежать в однiй площинi, то g ¹ паралельне перенесення

на ненульовий вектор, який паралельний цим прямим.

Доведення Нехай a, b i c попарно паралельнi iнварiантнi прямi руху g, якi не лежать в однiй площинi. Розглянемо яку-небудь площину ¾, перпендикулярну прямим a, b i c, та ¨¨ образ ¾ 0. Îñêiëüêè a ? ¾ i â ðóñi g пряма a переходить в себе, то a ? ¾ 0, òîìó ¾ i ¾ 0

площини.

7Доведення проводиться так, як i для випадку площини (див. стор. 44, теорема 1.24).

124

Позначимо через A; B; C i A0; B0; C0 точки перетину прямих a, b i c вiдповiдно з площинами ¾ i ¾ 0. Îñêiëüêè ¾ 7!g ¾ 0 i a, b i c iíâàðiàíòíi ïðÿìi, òî A 7!g A0, B 7!g B 0, C 7!g C 0. Позначимо

через B00 образ точки B0 в перетвореннi g. Âiäðiçêè BB0 i B0B00 ðiâíi, òîìó B0 середина âiäðiçêà BB00 (точка B00 не спiвпада¹ з точкою B, оскiльки в цьому випадку середина вiдрiзка BB0 ¹ iнварiантна точка, що протирiччить умовi леми).

 ðóñi g репер (B; A; C; B0) переходить в репер (B0; A0; C0; B00). Але при паралельному

p~ = ¡¡!

(

0)

(

0

0

0

00)

перенесеннi на вектор

AA0 репер

B; A; C; B

також переходить в репер

B

; A

; C

; B

,

òîìó ùî ¡¡!

= ¡¡! =

¡¡!

= ¡¡¡! =

AA0

BB0

CC0

B0B00

p~. Тому за лемою 2.5 рух g ¹ паралельне перенесення

на вектор p~.

¤

Ëåìà 2.8. Довiльний рух простору ма¹ принаймнi одну iнварiантну пряму.

Цю лему наводимо без доведення.

3 Класифiкацiя рухiв простору

Рухи простору, якi мають iнварiантнi точки. Класифiкацiя рухiв простору, якi немають жодно¨ iнварiантно¨ точки. Рухи першого i рухи другого роду.

По аналогi¨ з класифiкацi¹ю рухiв площини проведемо класифiкацiю рухiв простору в залежностi вiд наявностi iнварiантних точок.

1) Рух простору ма¹ принаймнi три iнварiантнi точки, якi не лежать на однiй прямiй.

Нехай A; B; C iнварiантнi точки руху g, що не лежать на однiй прямiй, AD пряма, перпендикулярна площинi ¾, яка проходить через iнварiантнi точки. Отже, площина ¾

ïðè ðóñi g переходить сама в себе, тобто

вона ¹ iнварiантною площиною. Оскiльки перпендикулярнiсть при русi зберiга¹ться, то, очевидно, пряма AD ¹ iнварiантною. Нехай

точка D цi¹¨ прямо¨ переходить при русi в точку D0, яка також належить данiй прямiй. Можливi

такi два випадки:

а) Точка D0 спiвпада¹ з точкою D. В цьому випадку репер R = (A; B; C; D) переходить сам

в себе. Але ж при тотожному перетворенi це репер також переходить сам в себе, тому згiдно леми 2.5 даний рух ¹ тотожним перетворенням простору. Ясно, що тотожне перетворення простору ¹ рух першого роду.

б) Точки D i D0 симетричнi вiдносно точки A. Перетворення g переводить репер R = (A; B; C; D) в репер R 0 = (A; B; C; D0), але ж симетрiя вiдносно площини ABC також переводить репер R â R 0, òîìó ðóõ g в даному випадку ¹ симетрiя вiдносно площини, яка проходить через три iнварiантних точки. Неважко бачити, що RjR 0 < 0, òîìó

симетрiя вiдносно площини рух другого роду.

2) Рух простору ма¹ принаймнi двi iнварiантнi точки A i B, але нема¹ iнварiантних точок, якi не лежать на прямiй AB.

В цьому випадку кожна точка прямо¨ AB ¹ iнварiантною точкою. Справдi, нехай M довiльна точка прямо¨ AB, à M0 ¨¨ образ. Оскiльки рух зберiга¹ просте вiдношення трьох

125

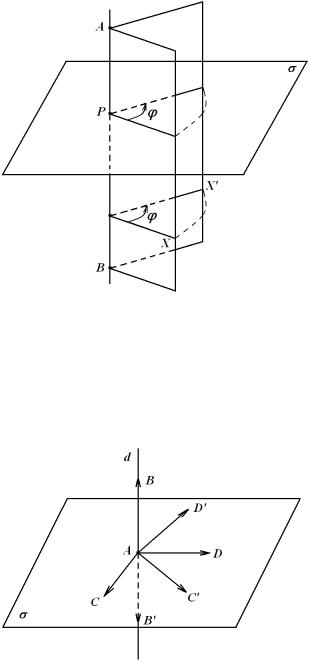
точок, то, очевидно, (AB; M) = (AB; M0), òîìó M = M0, тобто M iнварiантна точка. Отже, AB ¹ прямою iнварiантних точок.

Нехай ¾ довiльна площина, перпендикулярна до прямо¨ AB i яка перетина¹ ¨¨ в деякiй

òî÷öi P . Оскiльки площина ¾ ¹ iнварiантною

для даного 0руху, тому на нiй iндуку¹ться деякий рух g . Точка P ¹ ¹диною iнварiантною

точкою цього руху, отже, g0 поворот

навколо точки P на деякий кут ', ' =6 0.

Оскiльки довiльна площина, що проходить че- рез пряму AB, переходить в площину, яка

також проходить через цю пряму, то у всiх площинах, перпендикулярних до прямо¨ AB,

iндуку¹ться поворот з одним i тим же кутом повороту '.

Розглянутий нами рух назива¹ться поворотом простору навколо прямо¨ AB íà êóò '.

Пряма AB назива¹ться вiссю повороту, а кут ' кутом повороту. При цьому русi образ X0 точки X отриму¹ться ¨¨ обертанням навколо прямо¨ AB íà êóò ' в одному i тому ж напрямку незалежно вiд вибору точки X. Можна довести, що поворот простору навколо прямо¨ ¹ рух

першого роду.

Поворот простору навколо прямо¨ на кут ¼ назива¹ться симетрi¹ю вiдносно цi¹¨ прямо¨.

Вiдмiтимо, що тотожне перетворення також вважа¹ться поворотом навколо довiльно¨ прямо¨ на кут ' = 0.

3) Рух простору ма¹ тiльки одну iнварiантну точку A.

Згiдно леми 2.8 iсну¹ принаймнi одна iнварiантна пряма d. Ясно, що точка A лежить

íà ïðÿìié d, iнакше основа перпендикуляра, опущеного з точки A на пряму d, також була б

iнварiантною, що неможливо.

Позначимо чрез ¾ площину, яка проходить через точку A i перпендикулярна до прямо¨ d. Площина ¾ ¹ iнварiантною, тому рух g iндуку¹ на нiй деякий рух g0. Ðóõ g0 ì๠òiëüêè îäíó iнварiантну точку A, тому вiн ¹ поворот навколо точки A на деякий кут ', ' 6= 0.

Ортонормований репер R = (A; B; C; D) виберемо так, щоб точка B лежала на прямiй d, а точки C i D на площинi ¾. Îñêiëüêè B не ¹ нерухомою точкою, то точка B0 = g(B) буде симетричною точцi B вiдносно точки A. Â ðóñi g репер R = (A; B; C; D) переходить в репер R 0 = (A; B0; C0; D0) причому на площинi ¾ репери (A; C; D) i (A; C0; D0) орi¹нтованi однаково, тому репери R i R 0 орi¹нтованi протилежно. Це говорить про те, що g ¹ рух другого роду. Даний рух назива¹ться поворотним вiдображенням. Пряма d, êóò ', площина ¾ i точка

A називаються вiдповiдно вiссю, кутом, площиною i центром поворотного вiдображення.

Геометрично поворотне вiдображення ¹ добуток повороту навколо прямо¨ на симетрiю вiдносно площини.

ßêùî ' = ¼, то поворотне вiдображення ¹ симетрi¹ю вiдносно нерухомо¨ точки.

126

4) Рух простору нема¹ жодно¨ нерухомо¨ точки.

Нехай рух простору g нема¹ жодно¨ iнварiантно¨ точки, тодi за лемою 2.8 вiн ма¹ iнварiантну пряму d. За лемою 2.6 довiльна iнша iнварiантна пряма, якщо така iсну¹, паралельна прямiй d. Можливi такi три випадки:

а) Iснують принаймнi три попарно паралельнi iнварiантнi прямi, що не лежать в однiй площинi. В цьому випадку згiдно леми 2.7 даний рух ¹ паралельним перенесенням простору на деякий ненульовий вектор p~. Iнварiантними прямими ¹ тi i тiльки тi прямi

простору, якi паралельнi вектору p~. Очевидно, паралельне перенесення простору рух першого роду.

б) Iснують принаймнi двi паралельнi iнварiантнi прямi, а всi iншу iнварiантнi прямi, якщо такi iснують, лежать в площинi ¾, що проходить через цi прямi. В цьому випадку рух g

назива¹ться ковзним вiдображенням. Можна показати, g ¹ добутком вiдображення вiд площини ¾ на паралельне перенесення на ненульовий вектор p~, паралельний площинi ¾. Iнварiантними прямими ¹ тiльки тi прямi, якi лежать в площинi ¾ i паралельнi вектору

p~. Оскiльки вiдображення вiд площини ¹ рух другого роду, а паралельне перенесеннярух першого роду, то, очевидно, ковзне вiдображення рух другого роду.

â) Ðóõ g ма¹ тiльки одну iнварiантну пряму d. В цьому випадку g назива¹ться гвинтовим рухом. Можна довести, що g ¹ добутком повороту навколо прямо¨ d з кутом повороту

' 6= 0на паралельне перенесення на ненульовий вектор, паралельний прямiй d. Îñêiëüêè

поворот i паралельне перенесення рухи першого роду, то i гвинтовий рух ¹ рухом першого роду.

Таким чином iснують шiсть типiв рухiв простору, якi наведенi у наступнiй таблицi:

Рухи першого роду.

1) Паралельне перенесення на вектор p~.

а) Паралельне перенесення на вектор p~ 6= 0. б) Тотожне перетворення p~ = 0.

2) Поворот навколо прямо¨ на кут '.

а) Поворот на кут ', äå ' =6 0 i ' =6 ¼. б) Тотожне перетворення (' = 0).

в) Симетрiя вiдносно прямо¨ (' = ¼).

3) Гвинтовий рух.

Рухи другого роду.

4) Симетрiя вiдносно площини.

5) Поворотне вiдображення з кутом повороту ' =6 0.

а) Поворотне вiдображення з кутом повороту ', äå ' 6= 0 i ' 6= ¼.

а) Симетрiя вiдносно точки (' = ¼). 6) Ковзне вiдображення.

4 Перетворення подiбностi простору

Означення подiбностi простору. Властивостi подiбностi простору. Гомотетiя в просторi та ¨¨ властивостi. Подiбнiсть як добуток гомотетi¨ i руху.

127

Як i у випадку площини (див. стор. 55) перетворення простору назива¹ться перетворенням подiбностi або просто подiбнiстю, якщо iсну¹ таке число k > 0, ùî äëÿ

довiльних двох точок A i B та ¨х образiв A0 i B0 викону¹ться рiвнiсть A0B0 = kAB. Число k

назива¹ться коефiцi¹нтом подiбностi.

Ïðè k = 1 перетворення подiбностi зберiга¹ вiдстань, тобто воно ¹ рухом. Отже, рух

частинний випадок подiбностi. Прикладом перетворення подiбностi, вiдмiнного вiд руху, ¹ гомотетiя, яка в просторi вводиться так саме, як i для площини (див. стор. 55). Задамо точку M0 i дiйсне число m 6= 0. Êîæíié òî÷öi M поставимо у вiдповiднiсть точку M0 òàê, ùîá

¡¡¡!0 ¡¡¡!

M0M = mM0M:

Це вiдображення назива¹ться гомотетi¹ю з центром M0 i êîåôiöi¹íòîì M1 i M2 та ¨х образiв M10 i M20 з формули (2.75) отриму¹мо рiвнiсть

(2.75)

m. Для двох точок

¡¡¡¡!		=	1 2
1	2		¡¡¡¡!	(2.76)
M0	M0		mM M :

Звiдси виплива¹, що M10M20 = jmjM1M2. Таким чином, гомотетiя з коефiцi¹нтом m ¹

перетворенням подiбностi з коефiцi¹нтом k = jmj.

Виберемо ортонормований репер R = (O; E1; E2; E3) так, щоб точка O спiвпала з центром гомотетi¨. Якщо M(x; y; z) довiльна точка простору, а точка M0(x0; y0; z0) ¨¨ образ, то

очевидно,	x0 = mx; y0 = my; z0 = mz:	(2.77)

Тепер точно так, як це було зроблено для випадку площини, можна довести, що:

1.гомотетiя переводить площину (пряму), що не проходить через центр гомотетi¨, в паралельну площину (пряму);

2.гомотетiя переводить площину (пряму), яка проходить через центр гомотетi¨, в себе;

3.гомотетiя зберiга¹ просте вiдношення трьох точок прямо¨;

4.гомотетiя переводить вiдрiзок у вiдрiзок, промiнь у промiнь, напiвплощину у напiвплощину, напiвпростiр у напiвпростiр;

5.гомотетiя переводить кут в рiвний йому кут.

Доведемо, що гомотетiя з коефiцi¹нтом m зберiга¹ орi¹нтацiю простору при m > 0 i змiню¹ ¨¨ на протилежну при m < 0.8 Дiйсно, нехай (A; B; C; D) довiльний репер, а

(

A

; B

; C

; D

0)

його образ.За формулою (2.76) отриму¹мо: A0B0

mAB, A0C0

mAC,

0

0

0

¡¡! =

¡!

¡¡! =

¡!

A0D0

mAD, òîìó

¡¡! =

¡¡!

AB; AC; AD A0B0; A0C0; A0D0

¯

1

0

0

¯

3

0

1

0

:

(¡! ¡! ¡¡!)

(¡¡! ¡¡! ¡¡!) =

0

0

1

= m

j

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

Звiдси виплива¹ сформульоване вище твердження.

Аналогiчно, як i для площини, можна довести, що довiльне перетворення подiбностi простору з коефiцi¹нтом k ¹ добутком гомотетi¨ з тим же коефiцi¹нтом i довiльним

центром на деякий рух. Звiдси виплèâà¹, ùî:

8Нагада¹мо, що на площинi гомотетiя зберiга¹ орi¹нтацiю площини.

128

залишаються нерухомими. Якщо

коефiцi¹нтом стиску. Очевидно, всi точки площини

1.подiбнiсть простору переводить площину (пряму) в площину (пряму), паралельнi площини (прямi) у паралельнi площини (прямi);

2.подiбнiсть простору зберiга¹ просте вiдношення трьох точок прямо¨;

3.подiбнiсть простору переводить вiдрiзок у вiдрiзок, промiнь у промiнь, напiвплощину у напiвплощину, напiвпростiр у напiвпростiр;

4.подiбнiсть простору переводить кут в рiвний йому кут;

5.подiбнiсть простору зберiга¹ перпендикулярнiсть прямих та площин.

5 Афiннi перетворення простору

Означення афiнного перетворення простору. Стиск простору. Основна теорема афiнного перетворення простору. Афiннi перетворення простору першого i другого роду.

Перетворення простору назива¹ться афiнним, якщо воно довiльнi три точки M1, M2, M3,

що лежать на однiй прямiй, переводить в три точки M10, M20, M30, якi також лежать на однiй прямiй, i зберiга¹ ¨х просте вiдношення, тобто (M1M2; M3) = (M10M20; M30). Ясно, що довiльне перетворення подiбностi, зокрема довiльний рух, ¹ афiнним перетворенням.

Покажемо, що iснують афiннi перетворення, вiдмiннi вiд подiбностей. Задамо площину ¾ i додатне число k. Êîæíié òî÷öi M простору поставимо у вiдповiднiсть точку M0 òàê, ùîá

¡¡¡!		=	0
0	M0		¡¡¡!	(2.78)
M			kM M;

¡¡¡! 1 ¡¡¡!0,

äå M0 проекцiя точки M на площину ¾. З рiвностi (2.78) виплива¹, що M0M = k M0M тому кожна точка M0 ма¹ тiльки один прообраз.

Таким чином, побудоване вiдображення ¹ перетворенням простору; воно назива¹ться

стиском простору до площини ¾. Площина ¾ назива¹ться площиною стиску, а число k

¾

k < 1, то всi точки простору, що не лежать на площинi ¾, наближаються до площини, а якщо

k > 1, то всi точки простору вiддаляються вiд площини стиску, тобто ма¹ мiсце розтягування.

Доведемо, що стиск до площини ¹ афiнним перетворенням. Для цього виберемо прямокутну систему координат Oxyz так, щоб координатна площина Oxy спiвпала з

площиною ¾, i знайдемо аналiтичне вираження стиску з коефiцi¹нтом k до площини Oxy. ßêùî M(x; y; z) довiльна точка простору, а M0(x0; y0; z0) ¨¨ образ, то з означення стиску

виплива¹, що	x0 = x; y0 = y; z0 = kz:	(2.79)

Нехай M1(x1; y1; z1), M2(x2; y2; z2), M3(x3; y3; z3) три точки, якi лежать на однiй прямiй,

à M10(x01; y10 ; z10 ), M20(x02; y20 ; z20 ), M30(x03; y30 ; z30 ) ¨х образи. Якщо ¸ = (M1M2; M3), то за формулами (2.3) ма¹мо:

x3	=	x1 + ¸x2	;	y3	=	y1 + ¸y2	;	z3	=	z1 + ¸z2	:
	1 + ¸				1 + ¸				1 + ¸

Помноживши третю рiвнiсть на k i врахувавши формули (2.79), ми отрима¹мо:

x0

+ ¸x0

y0

+ ¸y0

z0

+ ¸z0

x30 =

1

2

;

y30 =

1

2

;

z30 =

1

2

:

1 + ¸

1 + ¸

1 + ¸

129

Звiдси виплива¹, що точки M10, M20, M30 лежать на однiй прямiй i (M10M20; M30) = ¸. Таким чином, стиск до площини ¹ афiнним перетворенням.

Неважко переконатись, що якщо k =6 1, то стиск до площини не ¹ подiбнiстю. Справдi,

розглянемо, наприклад, три точки O(0; 0; 0), E1(1; 0; 0) i E3(0; 0; 1) та ¨х образи O0(0; 0; 0),

E10 (1; 0; 0) i E30 (0; 0; k). ßñíî, ùî OE1 = O0E10 = OE3 = 1, O0E30 = k, òîìó O0E10 = 1 ¢ OE1, à O0E30 = k OE3.

Для афiнних перетворень простору ма¹ мiсце основна теорема, аналогiчна теоремi 1.32.

Ëåìà 2.9. Якщо афiннi перетворення f1 i f2 двi точки A i B переводять вiдповiдно в точки A0 i B0, òî f1(M) = f2(M), äå M довiльна точка прямо¨ AB.

Доведення цi¹¨ леми ми не да¹мо, оскiльки воно повнiстю спiвпада¹ з доведенням аналогiчно¨ леми 1.5.

Ëåìà 2.10. Якщо афiннi перетворення f1 i f2 три точки A, B i C, що не лежать на однiй прямiй, переводять вiдповiдно в точки A0, B0 i C0, òî f1(M) = f2(M), äå M äîâiëüíà

точка площини ABC.

Доведення. Нехай точка M довiльна точка площини ABC, вiдмiнна вiд точок A, B i C.

Доведемо, що f1(M) = f2(M). Проведемо через точку M прямi так, щоб вона перетинала якiнебудь двi з прямих AB, BC i CA в рiзних точках P i Q. За лемою 2.9 ма¹мо: f1(P ) = f2(P ), f1(Q) = f2(Q), тому за тi¹ю ж самою лемою f1(M) = f2(M).

Теорема 2.12 (основна теорема). Нехай R = (A; B; C; D) i R 0 = (A0; B0; C0; D0) äîâiëüíi

репери,0 тодi iсну¹ одне i тiльки одне афiнне перетворення простору, яке переводить репер R â R . При цьому всяка точка M з даними координатами в реперi R переходить в точку

M0 з тими ж самими координатами в реперi R 0.

Доведення. Розглянемо вiдображення f, яке довiльну точку M(x; y; z) в реперi R переводить в точку M0(x; y; z) в реперi R 0. Далi так саме, як при доведенi основно¨ теореми 1.32 про афiннi перетворення площини, доводимо, що f шукане афiнне перетворення.

Доведемо тепер, що коли f1 яке-небудь афiнне перетворення простору, яке переводить

репер R в репер R 0, òî f1 спiвпада¹ з f. Нехай M довiльна точка простору. Проведемо через

не¨ пряму так, щоб вона перетинала якi-небудь двi з площин, що мiстять гранi тетраедра ABCD в рiзних точках P i Q. За лемою 2.10 ма¹мо f(P ) = f1(P ), f(Q) = f1(Q). Çâiäñè,

використовуючи лему 2.9, отриму¹мо: f(M) = f1(M). Таким чином, вiдображення f i f1 спiвпадають, тобто f ¹дине афiнне перетворення, яке переводить репер R â R 0. При цьому

афiнному перетвореннi точка M(x; y; z)R переходить в точку M0(x; y; z)R 0.

Користуючись цi¹ю теоремою, можна довести, що афiнне перетворення простору переводить:

1.площину (пряму) в площину (пряму);

2.паралельнi площини (прямi) в паралельнi площини (прямi);

3.вiдрiзок у вiдрiзок, промiнь в промiнь, напiвплощину у напiвплощину, напiвпростiр у напiвпростiр.

130