Prak_Geom1

9 Перспективно-афiннi перетворення площини

Означення перспективно-афiнного перетворення площини та ¨х аналiтичне задання. Властивостi перспективно-афiнного перетворення. Косий стиск i зсув площини.

Означення 1.28.

Нетотожне афiнне перетворення назива¹ться перспективно-афiнним

(або рiдством), якщо воно ма¹ принаймнi двi нерухомi точки.

Знайдемо формули, за якими визнача¹ться перспективно-афiнне перетворення. Виберемо

репер R =

(O; E1

; E2) òàê, ùîá O i E1 були нерухомими точками даного перспективно-

афiнного перетворення f. Нехай E

2

f

E0

i E0

(k

; k)

R

. Îñêiëüêè O(0; 0)

f O(0; 0), а також

(1; 0) f

f

7! 2

2

1

7!

E

E

(1; 0), E

(0; 1)

E0 (k

; k), то за формулами афiнного перетворення (1.88)

1

7!

1

2

7!

2

1

отриму¹мо:

x0 = x + k1y;

y0 = ky:

(1.89)

Виходячи з формул (1.89) вiдмiтимо деякi властивостi перспективно-афiнного перетворення:

1±: Довiльна точка прямо¨, що проходить через двi нерухомi точки перспективноафiнного перетворення, буде нерухомою точкою.

Дiйсно, з формул (1.89) виплива¹, що кожна точка M(x; 0) прямо¨ OE1 переходить в точку M0(x; 0), тобто ¹ нерухомою точкою.

Означення 1.29. Пряма нерухомих точок назива¹ться вiссю перспективно-афiнного перетворення.

З наслiдку 1.8 виплива¹, що всi нерухомi точки перспективно-афiнного перетворення лежать на його осi.

2±: Прямi, якi з'¹днують вiдповiднi точки перспективно-афiнного перетворення, що не

лежать на його осi, паралельнi або спiвпадають.

Нехай

точка

M(x; y),

ùî

íå

лежить

íà

îñi

перспективно-афiнного

перетворення

переходить

â

точку

M0(x0

; y0).

Ç

формул

(1.89)

виплива¹, що

вектор

¡¡¡!

(k1y; (k

¡

1)y)

¡¡¡!

MM0

ìà¹

координати

. Ç

iншого

áîêó,

вектор

ìà¹

координати

(

1

¡

1)

2 2

; k

.

Таким чином,

E E0

k

¡¡¡! ¡¡¡!

вектори MM0 i E2E20 колiнеарнi. Звiдси i виплива¹ властивiсть 2±:

61

3±: Якщо пряма перетина¹ вiсь перспективно-афiнного перетворення в деякiй точцi, то

¨¨ образ проходить через цю точку; якщо ж пряма паралельна його осi, то ¨¨ образ також паралельний його осi.

Перше твердження очевидне (див. рис. на стор. 61, прямi MK i M0K0), а друге

твердження виплива¹ з того факту, що при афiнному перетвореннi паралельнi прямi переходять в паралельнi прямi (рис. на стор. 61, прямi a; b i a0; b0).

Зараз ми розглянемо два види афiнного перетворення, якi не ¹ перетвореннями подiбностi, це косий стиск i зсув площини.

Означення 1.30. Якщо прямi, що з'¹днують вiдповiднi точки перспективно-афiнного перетворення, не паралельнi осi, то таке перетворення назива¹ться косим стиском площини, а напрямки прямих, якi з'¹днують вiдповiднi точки, напрямком стиску.

У випадку косого стиску репер R = (O; E1; E2) можна вибрати так, щоб точки O i E1

належали осi a i E10 2 OE2. Тодi точка E20

ма¹ координати (0; k), тому формули (1.89)

набувають виду:

x0

= x;

y0

= ky;

(1.90)

äå k 6= 1. Формули (1.90) називаються формулами косого стиску. Коефiцi¹нт k

назива¹ться

¨¨ образ,

коефiцi¹нтом стиску i ма¹ такий змiст: якщо M довiльна точка площини, M0

(

)

M

0

MM0

¡¡¡! =

0

à

точка перетину прямо¨

ç âiññþ, òî

0

M0

¡¡¡!

0(

M

kM M. Дiйсно нехай M x; y , òîäi

) M

(x; 0)

¡¡¡!(0

)

0

(0

)

¡¡¡!0 =

0

M x; ky i

0

0

M0

¡¡¡!

; y . Звiдси виплива¹, що M M0

¡¡¡!

, òîìó M

; ky i M M

kM M.

Означення 1.31.

Якщо прямi, що з'¹днують вiдповiднi точки перспективно-афiнного

перетворення, паралельнi осi, то перетворення назива¹ться зсувом площини.

У випадку зсуву площини координатний репер

R

= (O; E1; E2) можна

вибрати

òàê, ùîá

точки O i E1 належали a, а точка E20

ìàëà á

координати (1; 1). В цьому випадку формули

(1.89) набувають виду:

x0 = x + y;

y0 = y:

(1.91)

¡¡!

i NN0 однаково напрямленi, якщо точки M

¡¡!

i P P 0 протилежно напрямленi, якщо M i P

Неважко бачити, що, користуючись формулами
(1.91), можна довести, що коли при зсувi M0 =
	(		)		N0 = f(N)		P 0 = f(P )			¡¡¡!
f		M		,		,		, то вектори MM0
i N лежать по один бiк вiд осi									a	¡¡¡!
										, i вектори MM0

лежать по рiзнi боки вiд прямо¨ a.

62

Косий стиск з вiссю a назива¹ться стиском до прямо¨ a, якщо напрямок стиску перпендикулярний до осi стиску i коефiцi¹нт стиску k додатнiй. При стиску до прямо¨ a всi точки цi¹¨ прямо¨ залишаються нерухомими, а кожна iнша точка M переходить в точку M0, розташовану на одному з нею перпендикулярi до осi a стиску по той же бiк вiд не¨, причому M0M0 = kM0M, äå M0 точка перетину прямих MM0 i a. ßêùî k < 1, то всi точки площини наближаються до осi стиску, а якщо k > 1, то всi точки площини вiддаляються вiд осi стиску (тобто фактично ма¹ мiсце розтягування).

10Група афiнних перетворень та ¨¨ пiдгрупи. Афiнна еквiвалентнiсть фiгур

Група афiнних перетворень та ¨¨ пiдгрупи. Афiнна еквiвалентнiсть фiгур. Теорема про афiнну еквiвалентнiсть чотирикутникiв.

Позначимо через A множину всiх афiнних перетворень площини. Доведемо, що коли

f1 2 A i f2 2 A, òî f2 ± f1 2 A. Äiéñíî, îñêiëüêè f1 i f2 перетворення, то f2 ± f1

перетворення. Але кожне з перетворень f1 i f2 переводить три точки, що лежать на однiй

прямiй, в три точки, що також лежать на однiй прямiй, i зберiга¹ ¨х просте вiдношення, тому перетворення f2 ± f1 володi¹ тими ж властивостями, тобто ¹ афiнним перетворенням. Отже,

f2 ± f1 2 A.

Äàëi, ÿêùî f 2 A, òî f¡1 2 A. Дiйсно, якщо точки A, B i C лежать на однiй прямiй, то ¨х образи A0 = f¡1(A), B0 = f¡1(B), C0 = f¡1(C) також лежать на однiй прямiй, iнакше якщо припустити протилежне, то знайдеться такий репер (A0; B0; C0), який при перетвореннi f переходить в три точки A; B; C, якi лежать на однiй прямiй, що неможливо.

Таким чином, множина A всiх афiнних перетворень утворю¹ групу. Вона назива¹ться

групою афiнних перетворень площини. Основним iнварiантом цi¹¨ групи ¹ просте вiдношення трьох точок.

Група P подiбностей ¹ пiдгрупою групи A; група D всiх рухiв також ¹ пiдгрупою

групи A. Iншими прикладами пiдгруп ¹: а) множина A1 всiх афiнних перетворень першого роду; б) множина A(M0) всiх афiнних перетворень, для яких M0 нерухома точка (група центро-афiнних перетворень); в) множина A(a) всiх афiнних перетворень, для яких пряма

a склада¹ться з нерухомих точок.

Означення 1.32. Ôiãóðè F i F 0 називаються афiнно-еквiвалентними, якщо iсну¹ таке афiнне перетворення f, ùî ôiãóðó F переводить у фiгуру F 0, тобто F 0 = f(F ).

З основно¨ теореми про афiнне перетворення виплива¹, що довiльнi два трикутники афiнно-еквiвалентнi. Використовуючи цей факт i те, що афiнне перетворення зберiга¹ просте вiдношення трьох точок прямо¨, легко довести, що довiльнi два паралелограми також афiнноеквiвалентнi. Однак для довiльних чотирикутникiв таке твердження нема¹ мiсця. Доведемо наступну теорему.

Теорема 1.34. Два чотирикутники афiнно-еквiвалентнi тодi i тiльки тодi, коли ¨х можна позначити через ABCD i A0B0C0D0, òàê ùîá

(AC; E) = (A0C0; E0); (BD; E) = (B0D0; E0);

(1.92)

äå E i E0 точки перетину прямих AC, BD i A0C0, B0D0.

63

Доведення. Нехай чотирикутники F i F 0 афiнно-еквiвалентнi, тобто iсну¹ таке афiнне перетворення f, ùî F 0 = f(F ). Позначимо цi чотирикутники лiтерами ABCD i A0B0C0D0 òàê, ùîá A0 = f(A), B0 = f(B), C0 = f(C) i D0 = f(D). Очевидно, пряма AC переходить в

пряму

A0C0, à BD â B0D0, òîìó E0 = f(E). Ïðè

афiнному перетвореннi зберiга¹ться просте
вiдношення трьох точок, тому мають мiсце
рiвностi (1.92).
Навпаки,	нехай	для чотирикутникiв
ABCD i A0B0C0D0 виконанi рiвностi (1.92).
Доведемо, що вони афiнно-еквiвалентнi.
Розглянемо	àôiííå	перетворення f,
яке репер	(A; B; C)	переводить в репер
(A0; B0; C0).
В силу рiвностi (AC; E) = (A0C0; E0) точка E переходить в точку		E0, тому пряма BE

переходить в пряму B0E0. Àëå îñêiëüêè (BD; E) = (B0D0; E0), то точка D переходить в точку D0. Таким чином, чотирикутники ABCD i A0B0C0D0 афiнно-еквiвалентнi.

64

P Q > F1F2, òî a > c. Ç

1.5Вивчення лiнiй другого порядку за канонiчними рiвняннями

1 Åëiïñ

Означення елiпса та виведення його канонiчного рiвняння. Дослiдження форми елiпса. Фокальнi радiуси елiпса та ексцентриситет. Побудова елiпса. Подiбнiсть елiпсiв. Рiвняння дотично¨ до елiпса.

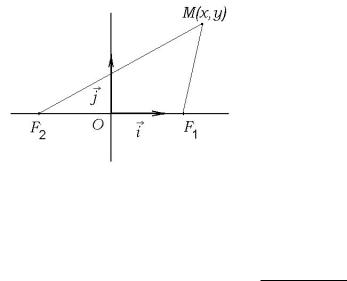
Означення 1.33. Елiпсом назива¹ться множина всiх точок площини, сума вiдстаней кожно¨ з яких до даних точок F1 i F2 дорiвню¹ довжинi даного вiдрiзка P Q, причому

P Q > F1F2.

Точки F1 i F2 називаються фокусами елiпса, а вiдстань мiж ними фокальною вiдстанню. Якщо M точка даного елiпса, то вiдрiзки F1M i F2M називаються фокальними радiусами точки M. Введемо позначення F1F2 = 2c, P Q = 2a. Îñêiëüêè

означення елiпса виплива¹, що коли фокуси спiвпадають, то елiпс ¹ колом радiуса a. В цьому

випадку фокуси спiвпадають з центром кола. Таким чином, коло ¹ частинний випадок елiпса.

Знайдемо

рiвняння

елiпса в прямокутнiй системi координат

~~,

äå

O

середина

1 2

~

· ¡¡!

Oi j

¡

âiäðiçêà

. Тодi фокуси

i

будуть мати координати

,

. Íå-

F F

F1

F2

F1

(c; 0)

, à i OF1

F2( c; 0)

õàé M(x; y) ¹ точка елiпса, тодi фокальнi радiуси цi¹¨ точ-

ки знаходяться за формулами:

F1M = p

; F2M = p

: (1.93)

(x ¡ c)2 + y2

(x + c)2 + y2

Згiдно з означенням 1.33 ма¹мо рiвняння F1M +F2M = 2a,

тобто

p

+ p

= 2a:

(x ¡ c)2 + y2

(x + c)2 + y2

ми отрима¹мо рiвняння:

Перенесемо другий радикал з лiво¨ частини у праву, тодi

p

= 2a ¡ p

(x ¡ c)2 + y2

(x + c)2 + y2

Пiднесемо обидвi частини цього рiвняння до квадрату. Пiсля зведення подiбних членiв
дiстанемо	ap(x ¡ c)2 + y2 = a2 ¡ cx:

Якщо ще один раз пiднесемо обидвi частини отриманого рiвняння до квадрату i зведемо подiбнi, то прийдемо до рiвняння

(a2 ¡ c2)x2 + a2y2 ¡ a2(a2 ¡ c2) = 0;

у лiвiй частинi якого сто¨ть многочлен другого степеня. Отже, елiпс ¹ алгебра¨чною лiнi¹ю
другого порядку19.
Якщо позначити a2 ¡ c2 = b2, то останн¹ рiвняння можна записати у виглядi
		x2	+	y2		= 1:	(1.94)
		a2			b2
19Алгебра¨чною лiнi¹ю другого порядку називають множину всiх							тих точок, координати (x; y) ÿêèõ
задовольняють рiвняння a11x2 + 2a12xy + a22y2 + 2a10x + 2a20y + a00							= 0; äå õî÷à áè îäèí ç êîåôiöi¹íòiâ
a11; a12; a22 íå äîðiâíþ¹ íóëþ.

65

Як результат ма¹мо, що коли обрано систему координат вище описаним способом, то координати будь-яко¨ точки елiпса задовольняють рiвняння (1.94).

Доведемо, що кожна точка M, координати (x; y) яко¨ задовольняють рiвняння (1.94),

належить елiпсу. Справдi, врахувавши, що

y2 = b2 µ1 ¡ x2 ¶; a2

матимемо:

b2

F1M = p(x ¡ c)2 + y2 = rx2 ¡ 2cx + c2 + b2

¡

x2 =

a2

= ra2 x2 ¡ 2cx + a2 =

ax ¡ a ;

(1.95)

c2

¯

c

¯

¯

¯

¯

¯

b2

F2M = p(x + c)2 + y2 = rx2 + 2cx + c2 + b2

¡

x2 =

a2

¯

¯

= r

c2

c

x2 + 2cx + a2 =

¯

¯

(1.96)

x + a

:

a2

a

А оскiльки для всiх точок, координати (x;

¯y) ÿêèõ¯

задовольняють рiвняння (1.94),

j

x

j

6 a,

то, врахувавши, що 0 <

c

< 1, ìà¹ìî

a

¯ax ¡ a¯ = a ¡ a x;

¯ax + a¯ = a + a x

(1.97)

c

c

c

c

. À öå¯

означа¹,¯

ùî

i

F1M + F2M = 2a

é

áóäü-¯яка точка,¯

координати яко¨ задовольняють

¯

¯

¯

¯

рiвняння (1.94) ¹ точкою елiпса.

Рiвняння (1.94) називають канонiчним рiвнянням елiпса. Через нього можна з'ясувати

цiлий ряд властивостей

åëiïñà. Òàê

ÿêùî

точка

M(x; y) належить елiпсу, то jxj

6 a i

jyj 6 b, тобто всi точки елiпса належать прямокутнику, сторони якого лежать на прямих з рiвняннями x = § a; y = § b.

Крiм того, разом з точкою M(x; y) елiпсу належать точки M0(x; ¡y), M00(¡x; y), M000(¡x; ¡y). Отже, елiпс ма¹ двi вза¹мно перпендикулярнi осi симетрi¨ (осi координат) i центр симетрi¨

66

(початок координат). Центр симетрi¨ називають центром елiпса, а точки перетину елiпса з осями симетрiй називають вершинами елiпса. Очевидно, що вершини елiпса мають координати: A1(a; 0), A2(¡a; 0), B1(0; b), B2(0; ¡b). Âiäðiçêè A1A2 i B1B2 ïðè a > b називають

вiдповiдно великою i малою вiссю елiпса, а числа a i b великою i малою напiвосями елiпса. Важливою характеристикою елiпса, заданого рiвнянням (1.94), ¹ число

	" =	c	;	(1.98)
		a

яке назива¹ться ексцентриситетом елiпса. Звiдси виплива¹, що ексцентриситет дорiвню¹ нулевi тодi i тiльки тодi, коли c = 0, тобто коли елiпс ¹ колом. Оскiльки

" = rc2 = s1 ¡ µb ¶2; a2 a

то очевидно, що	b		p
						(1.99)
				2
			=	1 ¡ " :
	a
Отже, ексцентриситет характеризу¹ форму				åëiïñà: ÷èì		" ближче до нуля, тим бiльше

елiпс схожий на коло, при збiльшеннi " елiпс ста¹ все бiльш сплющеним. Використовуючи

ексцентриситет i формули (1.95), (1.96), (1.97) фокальнi радiуси точки елiпса можуть тепер бути обчисленi за такими формулами:

F1M = a ¡ "x; F2M = a + "x:

(1.100)

Означення елiпса да¹ можливiсть вказати досить простий спосiб його побудови. Накреслимо на паперi прямокутну декартову систему координат та вiдмiтимо на нiй за координатами фокуси елiпса. Вiзьмемо шматок нитки довжиною 2a i ¨¨ êiíöi

закрiпимо у фокусах елiпса. Якщо вiдтягнути нитку кiнчиком олiвця i пересувати олiвець, тримаючи нитку весь час натягнутою, то олiвець накреслить елiпс з даними фокусами, довжина бiльшо¨ осi якого буде рiвна 2a.

Розглянемо iнший спосiб побудови елiпса, який можна виконати за допомогою циркуля та лiнiйки. Нехай A1A2 ¹ велика вiсь елiпса, а B1B2 ìàëà éîãî âiñü. Íà âiäðiçêàõ A1A2 i B1B2

як на дiаметрах побуду¹мо два концентричних кола !1 i !2, як показано на малюнку а) на

стор. 68. Проведемо ряд радiусiв великого кола. Через ¨х кiнцi проведемо прямi, паралельнi малiй осi, а через точки перетину цих радiусiв з меншим колом прямi, паралельнi великiй осi. Тодi точки перетину прямих, якi вiдповiдають одному i тому ж радiусу, будуть точками елiпса з заданими осями.

Для об рунтування цього способу побудови виберемо прямокутну систему координат, як показано на малюнку б) на стор. 68. Нехай h довiльний промiнь з початком O, M1 i M2

точки перетину цього променя з колами !1 i !2, а точка M(x; y) одна з побудованих точок. Позначимо через t кут мiж променями OA1 i h. Тодi точки M1 i M2 мають координати M1(a cos t; a sin t), M2(b cos t; b sin t). Оскiльки точки M i M1 мають рiвнi абсциси, а точки M i M2 рiвнi ординати, то

x = a cos t; y = b sin t:

(1.101)

67

ç êîåôiöi¹íòîì

З рiвностей (1.101) отриму¹мо

x2	+	y2	=	a2 cos2 t			+	b2 sin2 t		= cos2 t + sin2 t = 1;
a2		b2			a2				b2

тобто координати точки M(x; y) задовольняють канонiчне рiвняння елiпса xa22 + yb22 = 1.

à)

á)

Теорема 1.35. Åëiïñ ° з нерiвними напiвосями a i b ¹ образом кола !, побудованого на

великiй осi A1A2 елiпса, як на дiаметрi, при стиску площини до прямо¨ A1A2 стиску b

a .

Доведення. Нехай елiпс ° з напiвосями A1A2 i B1B2 в ортонормованому реперi (O; E1; E2) заданий канонiчним рiвнянням

x2 + y2 = 1: a2 b2

	Òîäi êîëî ! в цьому ж реперi буде мати таке рiвняння:
	x2 + y2 = a2. Стиск до прямо¨ A1A2								ç êîåôiöi¹íòîì k =	b
	зада¹ться формулами (1.90):								a
						x0 = x; y0 =	b	y;
тому образом кола ! ¹ ëiíiÿ x02 +	³b y0		´	= a2 àáî	a02		a
						+ b02 = 1, тобто елiпс °.
		a		2	x 2	y 2

Теорема 1.36. Два елiпса, ексцентриситети яких рiвнi, подiбнi.

Доведення. Нехай в ортонормованих реперах (O; E1; E2) i (O0; E10 ; E20 ) äàíi åëiïñè ° i °0, ексцентриситети яких рiвнi, мають вiдповiдно канонiчнi рiвняння: xa22 + yb22 = 1 i xa0022 + yb0022 = 1. Доведемо, що ° » °0.

Розглянемо рух f1, який репер (O; E1; E2) переводить в репер (O0; E10 ; E20 ). При цьому русi елiпс ° переходить в деякий елiпс °1, який в реперi (O0; E10 ; E20 ) ма¹ рiвняння xa22 + yb22 = 1, що виплива¹ з основно¨ теореми руху 1.22.

68

Åëiïñè ° i °0

мають рiвнi ексцентриситети ". За формулою (1.99) ма¹мо b = p

1

¡

"2

i

b0

p

, òîìó

a

b

a

1 ¡ "

2

a0

=

=

.

a0

b0

i êîåôiöi¹íòîì

a0

(O0; E0

; E0 ) зада¹ться формулами:

Гомотетiя f2

з центром O0

x0 = a0

x, y0 = a0

a в реперi

1

2

y (див. формули (1.84)) або x =

a

x0, y =

a

y0. Пiдставляючи цi значення в

a

a

a0

a0

y02

рiвняння елiпса °

1

ми отриму¹мо рiвняння його образа

x02

+

= 1, тобто елiпс °0. Îñêiëüêè

2

2

a0

b0

f1 i f2 ¹ перетворення подiбностi,.

òî f2 ± f1 ïîäiáíiñòü. Îòæå, ïîäiáíiñòü f2 ± f1 переводить

åëiïñ ° â åëiïñ °0, òîìó ° » °0

Знайдемо тепер рiвняння дотично¨ до елiпса, якùо вiн заданий канонiчним рiвнянням.

Нехай x22 +

y2

=

1; ¹ канонiчне

рiвняння

2

a

b

елiпса в прямокутнiй системi координат Oxy,

à M0(x0; y0) точка, яка належить йому.

Необхiдно знайти рiвняння дотично¨ до елiпса

з точкою дотикання M0. Нехай k0 ¹ кутовий

коефiцi¹нт дотично¨ d, тодi ¨¨ рiвняння буде

мати такий вид:

y ¡ y0 = k0(x ¡ x0):

(1.102)

Вiдомо, що дотична ¹ граничне положення сiч- но¨ M0M1 (= l), äå M1(x1; y1) точка елiпса,

ïðè óìîâi, ùî M1 ! M0. Запишемо рiвняння сiчно¨ l за двома точками:

l:	x ¡ x0	=	y ¡ y0	;
	x1 ¡ x0		y1 ¡ y0

çâiäêè

y1¡y0

(x ¡ x0)

, òîìó

y1¡y0

y ¡ y0 = x1¡x0

k = x1¡x0

¹ кутовий коефiцi¹нт сiчно¨. Отже,

k0 =

lim

k =

lim

y1 ¡ y0

:

(1.103)

M1!M0

M1!M0

x1 ¡ x0

Оскiльки точки M0; M1 належать елiпсу, то

xi2

+

yi2

= 1, äå i = 0; 1. Вiднiмаючи вiд другого

2

2

рiвняння перше, будемо мати x12¡x02

y12¡y02

a

b

(y1¡y0)(y1+y0)

, тобто (x1¡x0)(x1+x0)

, çâiäêè

a2

+

b2

= 0

a2

+

b2

= 0

y1 ¡ y0

=

b2

x1 + x0

:

(1.104)

Ç óìîâ (1.103) i (1.104) ìà¹ìî

x1 ¡ x0

¡a2 ¢ y1 + y0

k

=

lim k =

lim

y1 ¡ y0

=

lim

b2

x1 + x0

=

b2

2x0

=

b2x0

:

(1.105)

x1 ¡ x0

¡a2 ¢ y1 + y0

¡a2 ¢

2y0

0

M1!M0

M1!M0

M1!M0

¡a2y0

Пiдставляючи тепер значення k0 у рiвняння (1.102) ми будемо мати

y ¡ y0 = ¡

b2x0

(x ¡ x0);

a2y0

2

2

2

2

y0y2

2

2

2

2

звiдки отриму¹мо a y0(y¡y0) = ¡b

x0(x¡x0) àáî b

x0x+a

= b2 x0+a

y0. Подiливши обидвi

2

2 будемо мати x0x

y0y

x0

y0

частини отримано¨ рiвностi на a b

+

=

+

. Оскiльки точка M0(x0; y0)

a

2

b

2

a

2

2

належить елiпсу, то

x02

y02

b

+

= 1. Отже, рiвняння дотично¨ до елiпса в точцi M0(x0; y0) áóäå

2

2

a

b

таким:

x0x

+

y0y

= 1:

(1.106)

a2

b2

69

2 Гiпербола

Означення гiперболи та виведення ¨¨ канонiчного рiвняння. Фокальнi радiуси гiперболи та ¨¨ ексцентриситет. Асимптоти гiперболи та дослiдження ¨¨ форми. Подiбнiсть гiпербол. Рiвняння дотично¨ до гiперболи. Побудова гiперболи.

Означення 1.34. Гiперболою назива¹ться множина всiх точок площини, абсолютне значення рiзницi вiдстаней кожно¨ з яких до даних точок F1 i F2 дорiвню¹ довжинi даного

âiäðiçêà P Q, причому P Q < F1F2.

Точки F1 i F2 називають фокусами гiперболи, а вiдстань мiж ними фокальною вiдстанню. Оскiльки F1F2 > P Q > 0, то фокуси гiперболи рiзнi точки. Якщо M точка дано¨ гiперболи, то вiдрiзки F1M i F2M називаються фокальними радiусами точки M. ˆх довжини також будемо називати фокальними радiусами цi¹¨ точки. Нехай F1F2 = 2c,

P Q = 2a. Îñêiëüêè P Q < F1F2, òî a < c.

~~

, äå

середина

Знайдемо рiвняння гiперболи в прямокутнiй системi координат

1 2

~

· ¡¡!

Oi j

O

¡

âiäðiçêà

F F

OF1

. Тодi фокуси

F1

i

F2

будуть мати координати

F1(c; 0)

,

.

, à i

F2( c; 0)

Нехай M(x; y) ¹ точка гiперболи, тодi фокальнi радiуси обчислюються за формулами:

F1M = p

;

F2M = p

:

(1.107)

(x ¡ c)2 + y2

(x + c)2 + y2

За означенням 1.34 гiперболи ма¹мо рiвняння

jF1M ¡ F2Mj = 2a

àáî

¯p

¡ p

¯ = 2a:

(x ¡ c)2 + y2

(x + c)2 + y2

Останн¹ рiвняння запису¹ться¯

у виглядi

¯

¯

¯

p p

(x ¡ c)2 + y2 = 2a + (x + c)2 + y2;

ÿêùî F1M > F2M, i у виглядi

p p

(x + c)2 + y2 = 2a + (x ¡ c)2 + y2;

ÿêùî F1M < F2M. Скорочений варiант запису

p p

(x + c)2 + y2 = §2a + (x ¡ c)2 + y2:

Пiсля пiднесення обох частин рiвняння до квадрату i зведення подiбних матимемо

p

cx ¡ a2 = §a (x ¡ c)2 + y2:

Якщо ще раз пiднесемо до квадрату обидвi частини рiвняння, то прийдемо до рiвняння

(c2 ¡ a2)x2 ¡ a2y2 ¡ a2(c2 ¡ a2) = 0;

у лiвiй частинi якого сто¨ть многочлен другого степеня, а отже, гiпербола ¹ алгебра¨чною лiнi¹ю другого порядку.

Останн¹ рiвняння можна записати у виглядi

x2	y2			(1.108)
	¡		= 1;
a2		b2

70