Prak_Geom1

äå	c2 ¡ a2 = b2:	(1.109)

Отже, якщо обрано систему координат вище описаним способом, то координати будь-яко¨

точки гiперболи задовольняють рiвняння (1.108).

Доведемо, що кожна точка M, координати (x; y) яко¨ задовольняють рiвняння (1.108),

належить гiперболi. Справдi, врахувавши, що

y2 = b2

µa2 ¡ 1¶;

x2

матимемо:

F2M = p(x + c)2 + y2 = ¯ax + a¯:

(1.110)

F1M = p(x ¡ c)2 + y2 = ¯ax ¡ a¯;

¯

c

¯

¯

c

¯

А оскiльки для кожно¨ точки, координати¯

¯яко¨ задовольняють рiвняння¯

(1.108),¯

jxj > a, òî,

врахувавши, що c > a, äëÿ x < ¡a ìà¹ìî:

c

c

F1M = ¡

x + a; F2M = ¡

x ¡ a

a

a

i F1M ¡ F2M = 2a, à äëÿ x > a

c

c

F1M =

x ¡ a; F2M =

x + a

a

a

i F2M ¡ F1M = 2a. А це й означа¹, що будь-яка точка, координати яко¨ задовольняють

рiвняння (1.108), ¹ точкîю гiперболи. Рiвняння (1.108) називають канонiчним рiвнянням

гiперболи. Число " = ac називають

ексцентриситетîì ãiïåрболи. Оскiльки

c > a, òî

ексцентриситет гiперболи бiльший 1. Ясно, що " =

1 + ( b )2, çâiäêè b

p

"2

1

. Тепер

фокальнi радiуси точки гiперболи можуть бути записанiq

òàê:a

a

=

¡

F1M = "x ¡ a;

F2M = "x + a;

a;

ÿêùî x > 0;

)

(1.111)

F1M =

¡

"x + a;

F2M =

¡

"x

¡

ÿêùî x < 0:

Äîñëiäèìî

тепер

форму

гiперболи,

використовуючи канонiчне рiвняння (1.108).

Якщо точка M(x; y) належить гiперболi (1.108),

òî

jxj

>

a i точки

M0(¡x; y),

M00(x; ¡y),

M000(¡x; ¡y)

належать

гiперболi, тобто

гiпербола ма¹ двi вза¹мно перпендикулярнi

осi симетрi¨ (осi координат), центр симетрi¨

(початок координат), склада¹ться з двох

окремих гiлок, якi отримуються при x 6 ¡a

i x > a. Отже, всерединi смуги,

утворено¨

прямими A1M1 i A2M2

точок гiперболи нема¹

(OA1 = OA2 = a). Осi симетрi¨ називають

осями гiперболи: вiсь абсцис дiйсною (фокальною) вiссю, вiсь ординат уявною. Точки перетину A1(a; 0), A2(¡a; 0) гiперболи з

дiйсною вiссю називають вершинами, а числа a i b вiдповiдно дiйсною i уявною напiввiссю.

71

Розглянемо вза¹мне розташування прямо¨ l: y

=

kx,

що проходить через

початок

координат O з гiперболою (1.108). Пiдставляючи значення y в (1.108), ми отрима¹мо:

x2(b2 ¡ k2a2) = a2b2

:

(1.112)

Коренi цього рiвняння ¹ абсцисами точок перетину

прямо¨

з гiперболою. Якщо

2

¡k

2

2

,

2

l2

a

2

b

a

> 0

то пряма l ма¹ двi спiльнi точки з гiперболою, а якщо b

¡k

6 0, то рiвняння (1.112) нема¹

розв'язкiв, тобто пряма l не перетина¹ гiперболу. Отже, пряма y = kx перетина¹ гiперболу

òîäi i òiëüêè òîäi, êîëè b2 ¡ k2a2 > 0, тобто коли ¡ab < k < ab . Таким чином, всi точки гiперболи лежать у внутрiшнiх областях тих вертикальних кутiв, якi заштрихованi, тобто в областях -1 i -2.

Ïðÿìi y = ab x i y = ¡ab x називаються асимптотами гiперболи. Вияснимо, як розташованi вiтки гiперболи вiдносно асимптот. Нехай M(x; y1) довiльна точка гiперболи,

що знаходиться в першiй чвертi (x > 0; y1 > 0), à

N(x; y2) точка асимптоти l1, ÿêà

задана

рiвнянням y =

b

x. Знайдемо довжину вiдрiзка MN:

a

b

b p

b

p

2

2

2

2

MN = jy2 ¡ y1j =

x ¡

x

¡ a

=

(x ¡ x

¡ a ):

a

a

a

Помноживши тепер чисельник i знаменник на x + p

,

x2 + a2

отрима¹мо:

ab

MN =

x + p

:

x2 + a2

Ïðè

необмеженому

зростаннi

абсциси

x

точки M гiперболи довжина вiдрiзка MN,

монотонно

спадаючи,

пряму¹

äî

íóëÿ,

тобто

точка

M

необмежено

наближа¹ться

до асимптоти. Ця властивiсть да¹ наглядне

уявлення про розташування гiперболи вiдносно

асимптоти. На малюнку зображена гiпербола з

асимптотами.

Ïðè a = b гiпербола назива¹ться рiвнобiч-

ною, ¨¨ рiвняння ма¹

âèä x2

¡ y2

=

a2.

Очевидно, асимптоти

ðiâíîái÷íî¨

гiперболи

вза¹мно перпендикулярнi, тому ми можемо ¨¨

асимптоти прийняти за координатнi вiсi. Щоб

знайти рiвняння рiвнобiчно¨ гiперболи вiдносно

¨¨ асимп-

¼

тот, необхiдно повернути вихiдну систему координат на кут

Скориста¹мося для цього

¡

4 .

¼

формулами повороту навколо початку координат (1.33), тодi при ® = ¡

4

вони набувають

âèäó:

x0

+ y0

y0 ¡ x0

x =

; y =

:

p2

p2

Пiдставляючи тепер цi значення в рiвняння рiвнобiчно¨ гiперболи x

2

¡a2y

2

2, ми будемо

= a

a2

ìàòè (x0 +y0)2

¡

(y0

¡

x0)2

= 2a2, звiдки пiсля спрощень отрима¹мо x0y0 =

. Поклавши

= k,

2

2

k

рiвнобiчна гiпербола явля¹

будемо мати остаточно y0 =

, тобто стосовно координат x0 i y0

x0

собою графiк обернено¨ пропорцiйно¨ залежностi.

72

В цiй системi координат фокус

Використовуючи аналогiчнi мiркування, якi були зробленi для елiпса (див. теореми 1.35 i 1.36), можна довести справедливiсть таких двох теорем для гiперболи:

Теорема 1.37. Гiпербола з напiвосями a i b ¹ образом рiвнобiчно¨ гiперболи, яка ма¹ ту ж

äiéñíó âiñü A1A2, що i дана гiпербола, при стиску площини до прямо¨ A1A2 ç êîåôiöi¹íòîì

b a .

Теорема 1.38. Двi гiперболи, ексцентриситети яких рiвнi, будуть подiбними.

I нарештi, якщо гiпербола задана канонiчним рiвнянням					x2			y2
							¡		= 1 в прямокутнiй
					a2			b2
системi координат, а M0(x0; y0) точка, яка належить ¨й, то так саме, як i для елiпса (див.
стор. 69), виводиться рiвняння дотично¨ до гiперболи в цiй точцi:
x0x		y0y					(1.113)
		¡		= 1:
	a2		b2

Розглянемо спосiб побудови точок гiперболи, якщо вона задана фокусами F1 i F2, а також дiйсною вiссю A1A2. Накреслимо коло довiльного радiуса з центром в точцi F1, à ïîòiì

радiусом, який бiльше за вибраний на A1A2, накреслимо iнше коло з центром в точцi F2.

Точки перетину цих кiл, очевидно, лежать на гiперболi. Виконавши такi побудови декiлька разiв (вибираючи рiзнi радiуси), ми отрима¹мо ряд точок, якi належать гiперболi.

3 Парабола

Означення параболи та виведення ¨¨ канонiчного рiвняння. Подiбнiсть парабол. Побудова параболи. Рiвняння дотично¨ до параболи.

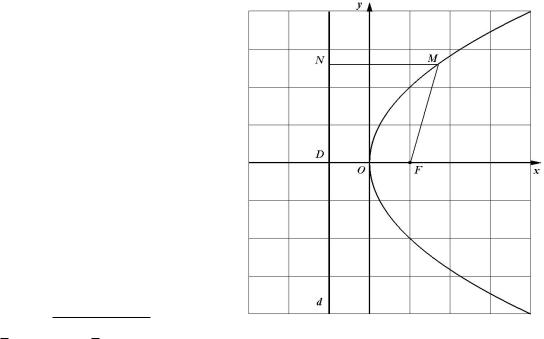
Означення 1.35. Параболою назива¹ться множина всiх точок площини, вiдстань кожно¨ з яких до дано¨ точки F дорiвню¹ вiдстанi до дано¨ прямо¨ d, що не проходить через F .

Точка F назива¹ться фокусом

параболи, а пряма d директрисою.

Вiдстань вiд фокуса до директриси познача¹ться через p i назива¹ться

фокальним	параметром параболи.
Таким чином, p = F D, äå D проекцiя
фокуса на директрису.
Знайдемо	рiвняння параболи		â
прямокутнiй системi координат		~~	, äå
	i	Oi j
		· ¡!
O середина вiдрiзка DF i ~		OF .

F ìà¹

координати (p2 ; 0), а директриса d рiвняння x+ p2 = 0. Нехай M(x; y) точка параболи. Тодi згiдно з означенням 1.35

½(M; d) = F M

àáî

¯¯¯x + p2¯¯¯ = r³x ¡ p2´2 + y2:

73

Пiсля пiднесення обох частин до квадрату i зведення подiбних членiв прийдемо до рiвняння

y2 = 2p x:

(1.114)

Доведемо, що кожна точка M,

координати x; y яко¨ задовольняють рiвняння (1.114),

належить параболi. Справдi, врахувавши, що y2 = 2p x, ìà¹ìî

p

2

p2

½(M; F ) = r³x ¡

´

+ y2 = rx2 ¡ px +

+ 2px =

2

4

¯x +

¯ = ½(M; d):

p

2

p

= r³x + 2´

=

2

¯

¯

¯

¯

А це й означа¹, що будь-яка точка, координати яко¨ задовольняють рiвняння (1.114) ¹ точкою параболи. Таким чином, ма¹мо ще одне означення параболи: ½Лiнiя на площинi назива¹ться параболою, якщо iсну¹ прямокутна декартова система координат, у якiй рiвняння цi¹¨ лiнi¨ ма¹ вигляд (1.114). Рiвняння (1.114) називають канонiчним рiвнянням параболи0 .

Якщо точка M(x; y) належить параболi (1.114), то x > 0 i точка M (x; ¡y) належить

параболi, тобто парабола ма¹ одну вiсь симетрi¨ (вiсь абсцис). Вiсь ординат парабола перетина¹ тiльки у точцi O(0; 0), яку називають вершиною параболи. Вiсь абсцис називають

вiссю параболи. Таким чином, парабола (1.114) розташована у напiвплощинi x > 0.

Теорема 1.39. Довiльнi двi параболи подiбнi.

Доведення. Нехай в ортонормованих реперах (O; E1; E2) i (O0; E10 ; E20 ) данi параболи ° i °0 мають вiдповiдно рiвняння: y2 = 2px i y02 = 2p0x0. Доведемо, що цi параболи подiбнi.

Розглянемо рух f1, який репер (O; E1; E2) переводить в репер (O0; E10 ; E20 ). При цьому русi

парабола ° переходить в деяку параболу °1, яка в реперi (O0; E10 ; E20 ) ма¹ рiвняння y2 = 2px.
Гомотетiя f2		з центром O0 i êîåôiöi¹íòîì p0	(O0; E0	; E0 ) зада¹ться формулами
x0 = p0 x, y0	= p0	p в реперi	1	2
		y. Образом параболи при цiй гомотетi¨ ¹ лiнiя y02 = 2p0x0, тобто парабола °0.
p	p

Îòæå, ïîäiáíiñòü f2 ± f1 переводить параболу ° в параболу °0, òîìó ° » °0.

Означення параболи дозволя¹ вказати наступний спосiб викреслювання ¨¨ частини за допомогою лiнiйки, косокутнього прямокутного трикутника й нитки. Нехай F фокус, а

d директриса			параболи.
Вiзьмемо	косокутник		й нитку,
довжина	ÿêî¨ ðiâíà		бiльшому
катету косокутника. Один кiнець
закрiпимо у фокусi, а другий
кiнець в вершинi гострого
êóòà K, який лежить проти
меншого		катета.	Çàêðiïèìî
вздовж директриси лiнiйку i до
не¨ приставимо меншим катетом
косокутник.		ßêùî	змiщувати
косокутник		вздовж лiнiйки, ут-

74

знаходиться за

M0M1

римуючи нитку натягнутою олiвцем, як вказано на малюнку, то кiнець олiвця буде описувати частину параболи. Дiйсно, KH = KM + MH i KH = KM + MF , òîìó MH = MF .

Розглянемо спосiб побудови точок параболи за допомогою циркуля та лiнiйки. Нехай F фокус, а

d директриса параболи. Проведемо через точку F

пряму, перпендикулярну до директриси. Побуду¹мо ряд прямих, паралельних до директриси. Знайдемо двi точки перетину кожно¨ з прямих з колом, центр якого знаходиться в фокусi параболи, а радiус дорiвню¹ вiдстанi вiд директриси до вiдповiдно¨ прямо¨. Отриманi точки, очевидно, будуть належати параболi.

Знайдемо тепер рiвняння дотично¨ до параболи, яка

~~

задана в прямокутнiй системi координат Oi j канонiчним рiвнянням y2 = 2px. Як нами вiдмiчалось на сторiнцi 69,

пiд дотичною ми розумi¹мо граничне положення сiчно¨. Рiвняння дотично¨ ми знаходимо за формулою (1.102), тобто y ¡ y0 = k0(x ¡ x0), äå k0 кутовий коефiцi¹нт дотично¨, а (x0; y0)

координати точки дотикання. Якщо M0(x0; y0) i M1(x1; y1) ¹ двi рiзнi точки, що належать параболi, то як вiдмiчалось на стор. 69, кутовий коефiцi¹нт сiчно¨

формулою k = y1¡y0

M0; M1 задовольняють рiвняння параболи,

x1¡x0 . Оскiльки координати точок

то ми ма¹мо двi рiвностi y02

= 2p x0 i y12 = 2p x1

, çâiäêè (y1 + y0)(y1

¡

y0) = 2p(x1

¡

x0), òîìó

y

y

2p

2p

1

¡

0 =

k =

M0

за точку дотикання, знайдемо k0:

y1+y0 . Îòæå,

x1¡x0

y1+y0 . Приймаючи

k0

= lim

k = lim

2p

=

2p

=

p

:

y1 + y0

M1!M0

y1!y0

2y0

y0

p

2

Таким чином, рiвнянням дотично¨ буде y ¡ y0 =

(x ¡ x0), çâiäêè y0y ¡ y0 = p(x ¡ x0), òîìó

y0

y0y = y02 + p(x ¡ x0) = 2px0 + px ¡ px0 = px + px0 = p(x + x0). Îòæå,

y0y = p (x + x0)

(1.115)

¹ рiвняння дотично¨ до параболи y2 = 2px з точкою дотикання, яка ма¹ координати (x0; y0) в прямокутнiй декартовiй системi координат.

4 Рiвняння елiпса, гiперболи i параболи в полярних координатах

Означення директрис для елiпса та гiперболи. Властивостi директрис. Ексцентриситет параболи. Рiвняння елiпса, гiперболи i параболи в полярних координатах.

Означення 1.36. Директрисами елiпса (гiперáоли) називаються двi прямi, якi паралельнi другiй осi i знаходяться вiд не¨ на вiдстанi a a áiëüøà (äiéñíà) íàïiââiñü, à "

ексцентриситет.

" , äå

Коло нема¹ директрис, оскiльки для нього " = 0. Директриси елiпса (гiперболи) будемо позначати через d1 i d2, причому d1 вiдповiда¹ фокусу F1(c; 0), à d2 фокусу F2(¡c; 0).

На рисунках а) i б) на сторiнцi 76 зображенi директриси елiпса						x2		y2
							+		= 1 i гiперболи
						25		9
	x2		y2
			¡		= 1.
25				9
			Доведемо, що директриси елiпса не мають спiльних точок з великою вiссю A1A2 åëiïñà,
тому вони не перетинають елiпс (див. рис. а)). Дiйсно, нехай D1						i D1		точки перетину

75

директрис d1 i d2 з фокальною вiссю елiпса. Тодi OA1 = OA2 = a, OD1 = OD2 = a" = ac2 . Îñêiëüêè c < a, òî OA1 < OD1 i OA2 < OD2. Звiдси виплива¹, що точки A1 i A2 належать

âiäðiçêó D1D2, тому директриси d1 i d2 не мають спiльних точок з вiдрiзком A1A2.

Аналогiчно можна довести, що директриси гiперболи перетинають дiйсну вiсь гiперболи, тому вони розташованi мiж двох гiлок гiперболи i не перетинають цi гiлки (див. рис. б)).

à)	x2		y2		á)		x2		y2
		+		= 1				¡		= 1
	25		9				25		9

Теорема 1.40. Елiпс (гiпербола) ¹ множина ° 0 всiх точок площини, таких, що вiдношення

вiдстанi кожно¨ точки вiд фокуса до вiдстанi вiд не¨ до вiдповiдно¨ директриси дорiвню¹ ексцентриситету.

Доведення. Доведення проведемо лише для випадку елiпса, оскiльки для гiперболи мiркування будуть цiлком аналогiчними. Отже, нехай ° ¹ даний елiпс, F1 перший фокус, а

d1 вiдповiдна йому директриса. В прямокутнiй системi координат точка F1 ма¹ координати

(c; 0), а директриса d1

ма¹ рiвняння x ¡ a"

= 0, òîìó ÿêùî M(x; y) точка площини, то

M¯

°¯

0

(p

¡

) + = " x

"

2

2

½(M; d1) =

¯

2 ¯

¡

x ¡ a"

, MF1 = (x ¡ c)2 + y2.

виплива¹¯

x y

, тобто

. Навпаки,

отрима¹мо

2

2p

c 2

2, çâiäêè¯

ßêùî

, òî

x

y2

¯

a

¯

. Пiдносячи цю рiвнiсть до квадрату, ми

(x ¡ c) + y = ("x ¡ a)

+

= 1

M 2 °

a2

b2

нехай M(x; y) 2 °, тодi за формулою (1.100) ма¹мо MF1 = a ¡ "x. З iншого боку,

1

) =

¯

x

¡

"

¯

"

½(M; d

¯

a

¯

= a ¡ "x;

¯

¯

òîìó MF1 = "½(M; d1), тобто M 2 ° 0. Отже, множина ° 0 спiвпада¹ з елiпсом °.

Дана теорема розкрива¹ геометричний змiст ексцентриситету елiпса та гiперболи, а саме: ексцентриситет елiпса або гiперболи ¹ стале число, яке дорiвню¹ вiдношенню вiдстаней вiд кожно¨ точки лiнi¨ вiд фокуса до вiдстанi вiд не¨ до вiдповiдно¨ директриси. З означення параболи видно, що для ¨¨ точок таке вiдношення також стале i дорiвню¹ одиницi, тому

число "одиниця" назива¹ться ексцентриситетом довiльно¨ параболи.

Позначимо через ° лiнiю, яка елiпсом, вiдмiнним вiд кола, або однi¹ю гiлкою гiперболи, або параболою. Нехай F i d фокус i вiдповiдна директриса цi¹¨ лiнi¨. За теоремою 1.40

ëiíiÿ ° ¹ множина всiх точок M напiвплощини, таких, що F M = "½(M; d), äå " ексцентриситет лiнi¨ °.

76

~

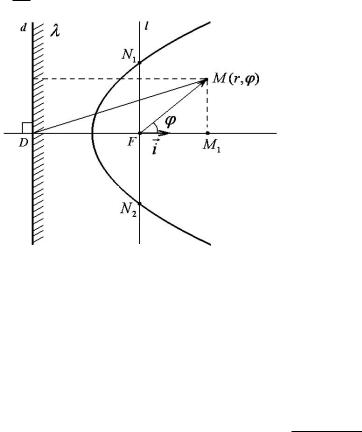
i =

~

Виведемо рiвняння лiнi¨ ° в полярнiй системi координат F i, полюсом яко¨ ¹ фокус F i

1 ¡¡!

DF DF , äå D проекцiя точки F на пряму d. Спочатку обчислимо ½(M; d), äå M(r; ') довiльна точка площини. Якщо M1 проекцiя

точки M на пряму F D, òî

\ ¡¡! ~ ½(M; d) = DM1 = DM ¢ cos MDF = DM ¢ i:

¡¡! ¡¡! ¡¡!

Àëå DM = DF + F M, òîìó

¡¡! ¡¡! ~ ¡¡! ~ ¡¡! ~ ½(M; d) = (DF + F M)i = DF ¢ i + F M ¢ i =

= DF + r cos ':

Точка M(r; ') належить лiнi¨ ° òîäi i òiëüêè òîäi,

êîëè F M = "½(M; d) àáî r = "(DF + r cos ').

Якщо покласти p = "DF , то звiдси отриму¹мо

r(1 ¡ " cos ') = p:

(1.116)

Це i ¹ рiвняння лiнi¨ ° (тобто елiпса, однi¹¨ вiтки гiперболи або параболи) в полярних координатах. З рiвняння (1.116) при ' = 90± àáî ' = ¡90± ìà¹ìî: r = p. Таким чином,

p полярний радiус точок N1 i N2, в яких перетина¹ться лiнiя ° з прямою l, що проходить через F i паралельна директрисi d. Число p назива¹ться фокальним параметром.

Рiвняння (1.116) записують ще у такiй формi

r =	p	:	(1.117)
	1 ¡ " cos '

Îòæå, ÿêùî " < 1, то рiвняння (1.117) визнача¹ елiпс, при " > 1 вiтку гiперболи, а при " = 1 визнача¹ параболу.

77

(x; y), взятих у

1.6 Загальна теорiя лiнiй другого порядку

1 Загальне рiвняння лiнi¨ другого порядку

Уявнi точки площини. Комплексна площина. Загальне рiвняння лiнi¨ другого порядку. Скорочена форма запису загального рiвняння. Приклади лiнiй 2-го порядку.

1. Вiдомо, що коли на площинi задана афiнна система координат, то кожнiй точцi M площини вiдповiда¹ пара дiйсних чисел (x; y), якi ¹ ¨¨ координатами у вибранiй системi координат. Отже, мiж точками площини i елементами множини R £ R, äå R множина

дiйсних чисел, iсну¹ вза¹мно однозначна вiдповiднiсть. Таким чином, надалi пiд точкою площини ми будемо розумiти пару дiйсних чисел.

Розширимо тепер поняття точки, розумiючи пiд точкою пару чисел

довiльному порядку, де (x; y) 2 C£C i C множина всiх комплексних чисел. Точка (x; y) áóäå

називатись дiйсною, якщо x; y дiйснi числа, i уявною, коли хоча б одне з них не ¹ дiйсним числом. Наприклад, серед точок A(3; ¡4), B(p3; i), C(¡p5; 7), D(¡p2; 1 + 3i) уявними ¹

точки B i D.

Якщо точка M в системi O~e1~e2 ма¹ координати (x; y), то в iншiй системi O0~e 01~e 02 âîíà матиме координати (x0; y0), якi визначаються за формулами (1.29). Оскiльки в цих формулах

êîåôiöi¹íòè c11, c12, x0, c21, c22, y0 дiйснi числа, то поняття уявно¨ точки не залежить

вiд вибору системи координат. Множину всiх дiйсних i уявних точок ми будемо називати

комплексною площиною.

Двi точки M1(x1; y1) i M2(x2; y2) називаються комплексно-спряженими, якщо ¨х вiдповiднi

координати ¹ комплексно-спряженi числа. Наприклад, A1(2 + 3i; 3 ¡ i) i A2(2 ¡ 3i; 3 + i) комплексно-спряженi точки. Пару точок A i B на комплекснiй площинi називають вiдрiзком

з кiнцями A i B. Серединою вiдрiзка з кiнцями M1(x1; y1) i M2(x2; y2) назива¹ться точка
¡	¢					M1(a + bi; c + di)	M2(a ¡ bi; c ¡ di)
M	x1+x2	;	y1+y2		. Цiкаво вiдзначити, що середина вiдрiзка з кiнцями в комплексно-спряжених
	2		2
точках ¹ дiйсна точка. Дiйсно, якщо						i		комплексно-

спряженi точки, то середина вiдрiзка M1M2 ¹ точка M(a; c), яка ¹ дiйсною, оскiльки a i c дiйснi числа.

2. Нехай O~e1~e2 ¹ афiнна система координат на площинi, тодi загальне рiвняння лiнi¨ другого порядку ма¹ вид:

a11x2 + 2a12xy + a22y2 + 2a10x + 2a20y + a00 = 0;

(1.118)

де коефiцi¹нти цього рiвняння ¹ довiльнi дiйснi числа, причому a11, a12, a22 одночасно не дорiвнюють нулю. Коефiцi¹нти a12, a10, a20 ми iнколи будемо позначати вiдповiдно через a21,

a01, a02.

Для зручностi в подальших мiркуваннях введемо такi позначення:

F (x; y) = a11x2 + 2a12xy + a22y2 + 2a10x + 2a20y + a00; F1(x; y) = a11x + a12y + a10;

F2(x; y) = a21x + a22y + a20;

F0(x; y) = a01x + a02y + a00:

Використовуючи цi позначення, рiвняння (1.118) скорочено можна записати так: F (x; y) = 0

àáî	F1	(x; y)x + F2(x; y)y + F0(x; y) = 0:	(1.119)

78

x2

y2

x2

y2

Прикладами

ëiíié

другого порядку ¹: елiпс

+

= 1, гiпербола

¡

= 1,

a2

b2

a2

b2

парабола y2 = 2px. Наведемо iншi приклади лiнiй другого порядку. Наприклад, лiнiя °, ÿêà

x2

y2

визнача¹ться рiвнянням

¡

= 0, ¹ лiнiя другого порядку. Це рiвняння можна записати

a2

b2

òàê:

³

x

y

´³

x

y

´

2

2

a

¡

b

a

+

b

y

= 0. В цьому випадку кажуть, що ° розпада¹ться на пару прямих, що

перетинаються:

x

x

y

¡

= 0 i

+

= 0. Аналогiчно лiнiя x

¡ a = 0, äå a 6= 0, розпада¹ться

a

b

a

b

на пару паралельних прямих: x ¡ a = 0 i x + a = 0. Âiäìiòèìî, ùî ëiíiÿ

другого порядку

x2

y2

x2+a2 = 0 ма¹ тiльки одну дiйсну точку (0; 0), а всi iншi ¨¨ точки уявнi, а лiнiя

+

+1 = 0

a2

b2

склада¹ться тiльки з уявних точок.

2 Перетин лiнi¨ другого порядку з прямою

Знаходження точок перетину прямо¨ з лiнi¹ю другого порядку. Дослiдження вза¹много розташування прямо¨ i лiнi¨ другого порядку.

Нехай в афiннiй системi координат O~e1~e2 задана лiнiя другого порядку ° загальним

рiвнянням	F (x; y) = a11x2 + 2a12xy + a22y2 + 2a10x + 2a20y + a00	= 0	(1.120)
i пряма l параметричними рiвняннями:
	x = x0 + p1t; y = y0 + p2t:		(1.121)

Знайдемо точки перетину прямо¨ l ç ëiíi¹þ °. Для цього пiдставимо значення x i y з рiвнянь (1.121) в рiвняння (1.120):

a11(x0 + p1t)2 + 2a12(x0 + p1t)(y0 + p2t) + a22(y0 + p2t)2 + 2a10(x0 + p1t) + 2a20(y0 + p2t) + a00 = 0;

звiдки, розкривши дужки, матимемо

a11(x20 + 2x0p1t + p21t2) + 2a12(x0y0 + x0p1t + y0p1t + p1p2t2) + a22(y02 + 2y0p2t + p22t2) +

+2a10(x0 + p1t) + 2a20(y0 + p2t) + a00 = 0:

Розкри¹мо тепер дужки i згрупу¹мо подiбнi члени при t2 i t:

(a11p12 + 2a12p1p2 + a22p22 )t2 + 2(a11x0p1 + a12x0p2 + a12y0p1

+ a22y0p2

+ a10p1

+ a20p2 )t +

|

} 0

|

{z

}

11

0

{z12

0 0

P

Q

+(a

x2

+ 2a

x y

+ a22y2

+ 2a10x0

+ 2a20y0 + a00 ) = 0:

(1.122)

|

{z

}

P; Q; R

R

Позначивши в (1.122) отриманi дужки вiдповiдно через

, ми отрима¹мо квадратне

рiвняння:

P t2 + 2Qt + R = 0;

(1.123)

äå P; Q; R означають такi вирази:

P = a11p21 + 2a12p1p2 + a22p22;

Q= a11x0p1 + a12x0p2 + a12y0p1 + a22y0p2 + a10p1 + a20p2 =

=(a11x0 + a12y0 + a10)p1 + (a21x0 + a22y0 + a20)p2 = F1(x0; y0)p1 + F2(x0; y0)p2;

R = F (x0; y0):

79

Знайшовши з рiвняння (1.123) параметри t1; t2 точок перетину i пiдставивши ¨х в рiвняння

(1.121), отрима¹мо координати точок перетину. Вiдмiтимо, що кожному кореню рiвняння
(1.123) вiдповiда¹ точка перетину, причому рiзним кореням вiдповiдають рiзнi точки: дiйсним
кореням дiйснi точки, а уявним кореням уявнi точки.
Проведемо дослiдження рiвняння (1.123). Можливi дваp випадки. p
1)	P 6= 0	. Рiвняння (1.123) ма¹ два коренi:	t1 =	¡Q+ ±	¡Q¡ ±	± = Q	2	¡ P R	¹
				P , t2 =	P , äå

дискримiнант рiвняння (1.123). Якщо ± > 0, то пряма l перетина¹ лiнiю ° в двох дiйсних

рiзних точках M1 i M2; ïðè ± < 0 в двох комплексно-спряжених точках, i в двох дiйсних спiвпадаючих точках, коли ± = 0. На рисунку а) пряма l1 вiдповiда¹ випадку ± > 0, пряма l2 випадку ± < 0, а пряма l3 випадку ± = 0.

a)

á)

â) ã)

2) P = 0. Рiвняння (1.123) набува¹ вигляду: Qt+R = 0. ßêùî Q 6= 0, то пряма l перетина¹ лiнiю ° в однiй точцi (пряма l на рисунку б) або на рисунку в)). Якщо Q = 0, R 6= 0, то пряма l íå ì๠ç ëiíi¹þ ° жодно¨ спiльно¨ точки нi дiйсно¨, нi уявно¨ (прямi m i m0 íà ðèñ. á)

àáî ïðÿìi m1, m2, m3. . . на рис. г)). Якщо, нарештi, Q = R = 0, òî äîâiëüíå t ¹ розв'язком рiвняння (1.123), тому l ½ ° (ïðÿìi n i n0 на рисунках в) i г)).

80