Степенные ряды. Интервал сходимости степенного ряда. Разложение функций в степенные ряды.

Степенным рядом называется ряд вида:

,

где называются коэффициентами степенного ряда.

Придавая х различные числовые значения, будем получать различные числовые ряды, которые могут оказаться сходящимися или расходящимися. Множество тех значений х, при которых степенной ряд сходится, называется областью его сходимости. Это множество всегда не пусто, так как любой степенной ряд сходится при .

Очевидно, что частичная сумма степенного ряда

является функцией переменной х. Поэтому и сумма ряда S также является некоторой функцией переменной х, определенной в области сходимости ряда: .

Рассмотрим теорему, имеющую важное значение в теории степенных рядов и касающуюся области сходимости степенного ряда.

Теорема Абеля. (Абель Нильс Хенрик (1802—1829) — норвежский математик).

1) Если степенной ряд сходится при , то он сходится, и притом абсолютно, для всех х, удовлетворяющих условию ;

2) если степенной ряд расходится при , то он расходится для всех х, удовлетворяющих условию .

Теорема Абеля утверждает, что если - точка сходимости степенного ряда, то во всех точках, расположенных на интервале () этот ряд сходится абсолютно, а если -точка расходимости степенного ряда, то во всех точках, расположенных вне интервала () ряд расходится.

Отсюда вытекает следующая теорема:

Если ряд сходится не при всех значениях х и не только при , то существует числотакое, что ряд абсолютно сходится при и расходится npu .

Интервал называетсяинтервалом сходимости степенного ряда. Число R называется радиусом сходимости степенного ряда. Отметим, что интервал сходимости у некоторых рядов охватывает всю числовую прямую (в этом случае пишут ), у других вырождается в одну точку ().

Итак, всякий степенной ряд имеет свой радиус сходимости R. При ряд может либо сходиться, либо расходиться. Этот вопрос решается для каждого конкретного ряда.

Приведем способ определения радиуса сходимости степенного ряда по признаку Даламбера.

Если существует предел ,то радиус сходимости ряда равен .

Свойства степенных рядов.

Пусть функция является суммой степенного ряда

,

интервал сходимости которого .

В этом случае говорят, что на интервале функция разлагается в степенной ряд (или в ряд по степеням х).

Имеют место две теоремы о свойствах степенных рядов.

8. Если функция 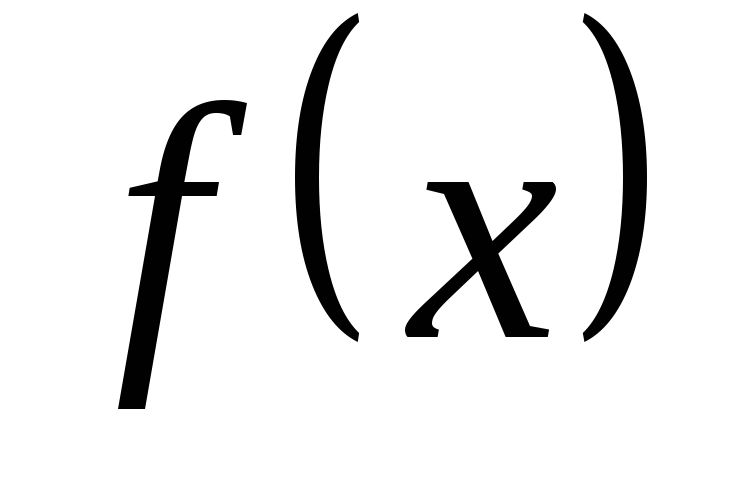на интервале разлагается в степенной ряд, то она дифференцируема на этом интервале и ее производная может быть найдена почленным дифференцированием ряда, т.е.:

.

Аналогично могут быть вычислены производные любого порядка функции . При этом соответствующие ряды имеют тот же интервал сходимости, что и степенной ряд.

9. Если функция на интервале разлагается в степенной ряд, то она интегрируема в интервале и интеграл от нее может быть вычислен почленным интегрированием степенного ряда, т.е., если , то:

+

++ … ++....

Теорема. Если функция на интервале разлагается в степенной ряд:

,

то это разложение единственно.

Пусть функция бесконечное число раз дифференцируема в точке, тогда в окрестности этой точки функция раскладывается в степенной ряд:

,

называемый рядом Тейлора.

При функцияразлагается в степенной ряд:

,

называемый рядом Маклорена.

Для того чтобы ряд Маклорена сходился на и имел своей суммой функцию, необходимо и достаточно, чтобы на остаточный член формулы Маклорена стремился к нулю при ,т.е. для любого .

Рассмотрим разложения в ряд Маклорена некоторых элементарных функций:

;

;

;