Двойные и тройные интегралы.

Вычисление двойного интеграла по области от функции производится по формуле

, (38)

если область определяется неравенствамии по формуле

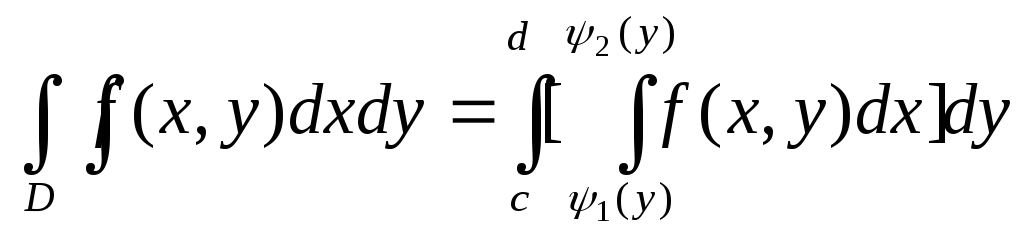(39)

если область определяется условиями

Вычисление тройного интеграла аналогично формулам (38), (39) к нахождению трех повторных определенных интегралов. Значения двойного или тройного интеграловиравны, соответственно, площади плоской фигурыи объему тела.

Векторные и скалярные поля

Векторное поле характеризуется такими величинами, как дивергенция, ротор, поток, циркуляция.

Дивергенцией векторного поля называется скалярная величина , а его ротором вектор – функция вида

Потоком векторного поля через поверхность σ в направлении нормали называется значение поверхностного интеграла

где единичный нормальный вектор поверхности. , , углы между и соответственно. Вычисление поверхностного интеграла сводится к вычислению двойного интеграла. Пусть уравнение поверхности σ можно написать в виде Через обозначим проекцию σ на плоскости . Тогда

(41)

При этом перед двойным интегралом берется знак плюс, если . аналогично вычисляются интегралы

и приведенные в правой части (40).

Циркуляцией векторного поляназывается криволинейный интеграл по замкнутой кривой

Теорема Стокса устанавливает связь между циркуляцией векторного поля вдоль замкнутой кривой и его ротором.

, (42)

где σ- поверхность, ограниченная кривой - единичный нормальный вектор к этой поверхности. Направление вектора и обхода контура должны быть согласованы. Формула (42) связывает также криволинейный и поверхностный интегралы.

Теорема Остроградского выражает связь между потоком векторного поля через замкнутую поверхность в направлении внешней нормали и дивергенцией поля:

(43)

где – тело , ограниченное поверхностью σ.

Криволинейные интегралы

Вычисление криволинейного интеграла вдоль кривойот функции и cводится к нахождению определенных интегралов:

1. Если кривая задана уравнением , и – абсциссы крайних точек , дифференцируема, то

(36)

2. Если кривая задана параметрическими уравнениями , где ,дифференцируемые функции, то

(37)

Лекция 30

Основы теории вероятности.

Случайные события. Определение вероятности.

Случайным событием называется событие, которое при выполнении некоторого комплекса условий может произойти или не произойти. Будем рассматривать случайные события, которые обладают так называемой статистической устойчивостью или, иначе, устойчивостью частот.

Определение. Событие называется достоверным в данном испытании, если оно неизбежно происходит при этом испытании.

Определение. Событие называется невозможным в данном испытании, если оно заведомо не происходит в этом испытании.

Примем как аксиому, что для каждого события Аможно определить, по крайней мере теоретически, вероятность этого события – числоР(А), представляющее, в некотором смысле «меру достоверности» данного события и подчиненное естественным требованиям. Предполагается, что вероятность любого события удовлетворяет неравенству

причем вероятность невозможного  события равна нулю, а вероятность достоверного события  равна единице.

Определение. Под суммой двух событий А и В понимается событие

которое имеет место тогда и только тогда, когда произошло хотя бы одно из событий А и В.

Определение. Произведением двух событий А и В называется событие

состоящее в одновременном появлении как события А, так и события В.

Определение. Под вероятностью Р(А) события А понимается отношение числа равновозможных элементарных исходов, благоприятствующих событию А, к общему числу всех равновозможных и единственно возможных элементарных исходов данного испытания.

Таким образом, если m – число элементарных исходов, благоприятных событию А и n – общее число всех элементарных исходов при данном испытании, и все эти исходы равновозможны, то на основании определения имеем формулу

.

Так как, очевидно, , то , т.е. вероятность любого события есть неотрицательное число, не превышающее единицы.

Из определения вероятности вытекают следующие основные ее свойства.

10. Вероятность невозможного события равна нулю.

Действительно, если событие А невозможно, то число благоприятных ему элементарных исходов m=0, и мы имеем

.

2. Вероятность достоверного события равна единице.

В самом деле, если событие А достоверно то, очевидно m=n и, следовательно,

.

Определение. Два события А и В называются равными, если каждое из них происходит всякий раз, когда происходит другое и обозначается A=В.

Теорема 1. Равные события имеют равные вероятности, т.е. если А=В, то

Р(А)=Р(В).

Определение. Говорят, что из события А следует событие В , если событие В появляется всякий раз, как только произошло событие А.

Теорема 2. Если , то .

Определение. Событие , происходящее тогда и только тогда, когда не происходит событие А, называется противоположным последнему.

Например, если при бросании монеты событие А есть выпадение герба, то событие представляет собой не выпадение герба, т.е. выпадение решетки.

Из определения 4 следует, что 1) А+ достоверно; 2) А невозможно.

Теорема 3. Вероятность противоположного события равна дополнению вероятности данного события А до 1, т.е.

.