
- •Математическая логика и теория алгоритмов
- •11. Понятие об алгоритмах. Схемы алгоритмов
- •11.1. Понятие об алгоритме и теории алгоритмов
- •11.2. Схемы алгоритмов
- •11.3. Рекурсивные функции
- •11.4. Машина Тьюринга
- •11.5. Машина Поста
- •11.6. Нормальные алгорифмы а.А. Маркова
- •11.7. Универсальная абстрактная машина
- •11.8. Разрешимость в теории алгоритмов. Проблема самоприменимости
- •11.9. Сложность алгоритма
- •11.10. Представление схемы алгоритма эквивалентным автоматом
- •11.11. Представление схемы алгоритма микропрограммой с двумя типами микрокоманд
- •12. Элементы формальной логики
- •12.1. Предмет формальной логики
- •12.2. Понятие и его виды
- •12.3. Отношения между понятиями
- •12.4. Операции над понятиями
- •12.5. Суждение и его характеристика
- •Модальные и категорические суждения.
- •Простые категорические суждения.
- •Виды простых категорических суждений.
- •Распределение терминов в простом категорическом суждении.
- •Логический квадрат.
- •13. Умозаключение
- •13.1. Виды умозаключений
- •13.2. Непосредственное умозаключение
- •Умозаключения путем противопоставления предикату.
- •13.3. Опосредованное дедуктивное умозаключение. Фигуры силлогизма
- •Фигуры пкс.
- •Модусы пкс.
- •13.4. Дополнительные виды силлогизмов
- •13.5. Индуктивные умозаключения. Математическая индукция
- •14. Логика высказываний
- •14.1. Семантика логики высказываний
- •I закон – тождества.
- •14.3. Формализация высказываний
- •14.4. Интерпретации, разрешимость, выполнимость, общезначимость
- •14. 5. Логическая равносильность. Законы логики
- •14.6. Формы представления формул логики высказываний
- •14.7. Проблема дедукции в логике высказываний
- •15. Проверка правильности логических выводов. Метод резолюций
- •15.1. Закон контрапозиции
- •15.2. Логическое следование. Проверка правильности логических выводов
- •15.3. Силлогизмы в логике высказываний
- •Разделительно-категоричные силлогизмы.
- •16. Синтаксис и семантика языка логики предикатов
- •16.1. Понятие предиката
- •16.2. Кванторы и связанные переменные
- •16.3. Синтаксис языка логики предикатов. Формулы логики предикатов и формализация суждений
- •16.4. Семантика формул логики предикатов
- •Общезначимость, выполнимость, невыполнимость.
- •17. Тождественные преобразования формул логики предикатов
- •17.1. Операции над предикатами
- •17.2. Основные равносильности логики предикатов
- •Отрицание предложений с кванторами.
- •17.3. Тождественные преобразования формул
- •17.4. Универсум Эрбрана
- •18. Использование метода резолюций в логике предикатов
- •18.1. Подстановка и унификация
- •18.2. Резольвенция и факторизация
- •18.3. Метод резолюций в логике предикатов
- •18.4. Принцип логического программирования
- •19. Логические исчисления
- •19.1. Понятие о формальных теориях
- •19.2. Исчисление высказываний
- •19.3. Исчисление предикатов
- •19.4. Система натурного вывода
- •19.5. Понятие о математической лингвистике
- •19.6. Формальный язык
- •19.7. Формальные грамматики и их свойства
- •19.8. Теоремы Гёделя
- •20. Неклассические логики
- •20.1. Современные модальные логики
- •20.2. Понятие о теории неопределенности
- •20.3. Элементы теории нечетких множеств и нечеткая логика
- •20.4. Нечеткие алгоритмы
- •Литература
- •Приложение 1 Варианты контрольных заданий по дисциплине «Дискретная математика»
- •Приложение 2 Варианты контрольных заданий по дисциплине «Математическая логика»
19.2. Исчисление высказываний
Исчисление высказываний является простым примером формальной аксиоматической теории [19]. Порождение тождественно-истинных высказываний и является основной задачей исчисления высказываний.
Построим формальную аксиоматическую теорию исчисления высказываний в одном из возможных ее вариантов.
1. Алфавит исчисления высказываний состоит из:
а) высказывательных переменных, которые будем обозначать прописными буквами X,Y,…,Z;
б) символов логических операций, из которых выберем импликацию и инверсию ¯ (можно показать, что такая система соответствующих логических функций является функционально полной);
в) скобок (, ).
2. Формулы исчисления высказываний:
а) все переменные – формулы;
б)
если А и В – формулы, то (![]() )
и (АВ)
тоже формулы.
)
и (АВ)
тоже формулы.
Пример. Пусть А,В,С – формулы.
Тогда:
(С(АВ)),
(((![]() )В)(
)В)(![]() ))
– тоже формулы.
))
– тоже формулы.
Для сокращения записи опустим в формуле внешние скобки и те пары скобок, которые относятся к инверсии:
С(АВ),
(![]() В)
В)![]() .
.
3. Аксиомы исчисления высказываний.
Аксиомы должны обеспечивать порождение всех тождественно истинных высказываний.
Рассмотрим одну из возможных систем аксиом, содержащую всего три аксиомы.
А1. А(ВА);
А2. (А(ВС))((АВ)(АС));
А3.
(![]()
![]() )((
)((![]() А)В).
А)В).
По сути А1-А3 – схемы аксиом, поскольку они порождают бесконечное множество формул, учитывая правило подстановки.
4. Правила вывода.
1) Правило подстановки.
Если Х – выводимая формула, содержащая букву А (обозначим Х(А)), то выводима и формула Х(В), получающаяся из Х заменой всех вхождений А на произвольную формулу:
![]() ;
;
2) Правило заключения.
Это правило называют Modus Ponens или сокращенно m.p:
![]() .
.
Строго говоря, в правилах вывода использованы также схемы формул (метаформулы).
Рассмотрим аксиомы и убедимся в их тождественной истинности (тавтологичности, еще говорят – общезначимости).
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом, все аксиомы, как и следовало ожидать, тождественно истинны, хотя мы и говорили, что аксиомы недоказуемы. Будем считать, что мы использовали метадоказательства.
Проиллюстрируем
вывод формулы исключенного третьего
А![]() или АА,
т.е. докажем
или АА,
т.е. докажем
![]() А├А
для любой формулы А.
А├А
для любой формулы А.
1. Возьмем аксиому А2 и подставим формулу АА вместо В и формулу А вместо С, в соответствии с правилом подстановки:
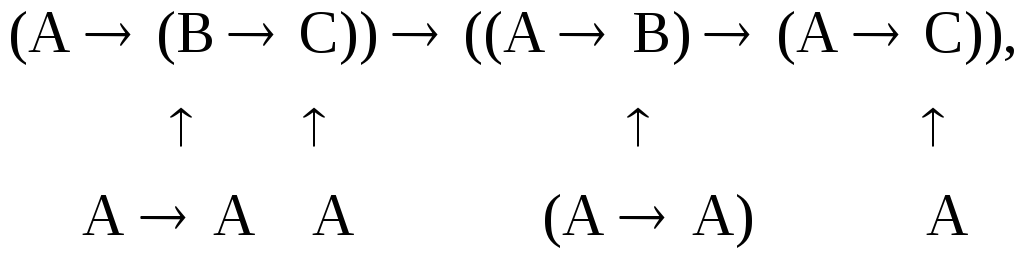
Получим:
(А((АА)А))((А(АА))(АА)).
2. Подставим в А1(АА) вместо В:
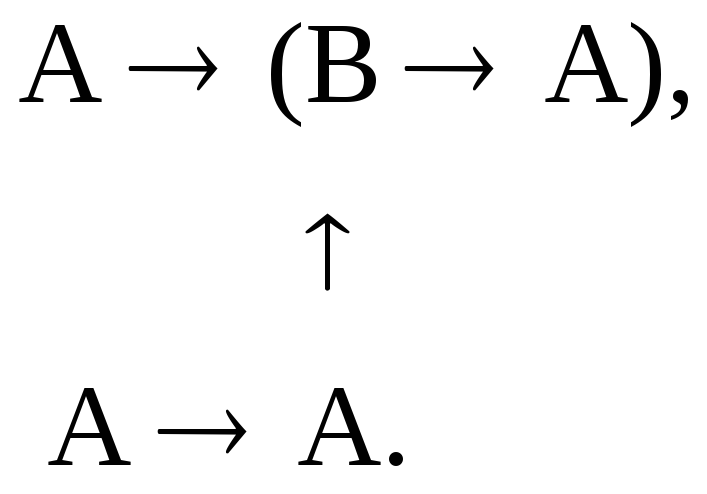
Получим:
А((АА)А).
3. Обратим внимание, что это выражение является левой частью импликации, полученной после первого шага, то есть по правилу m.p:
![]() ,
,
получаем ((А(АА))(АА)), т.е. выражение под чертой.
4. Подставим теперь в А1 формулу А вместо В:
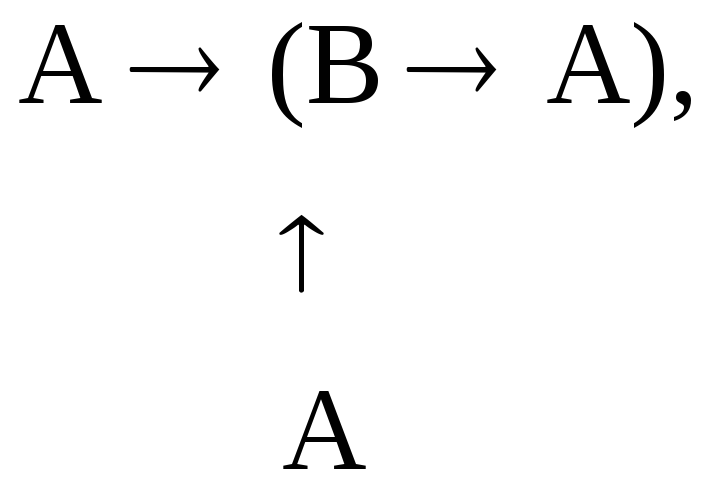
получим А(АА).
5. Обратим внимание, что это выражение также является левой частью выражения, полученного в результате третьего шага, то есть по правилу m.p:
![]() ,
,
получаем ├АА, что и требовалось доказать. Поскольку вывод формулы был получен из аксиом А1-А2, то (АА), т.е. формула (АА) общезначима.
Аналогично могут быть выведены другие тождества логики высказываний.
Более строго, в исчислении высказываний [19]:
1) всякая выводимая (из пустой системы гипотез) формула исчисления высказываний тождественно истинна;
2) если формула А исчисления высказываний является тождественно истинной, то она выводима.
Формальную
аксиоматическую теорию называют
непротиворечивой, если не существует
формулы А такой, что одновременно
выводимы А и
![]() .
.
В математической логике доказывается, что исчисление высказываний непротиворечиво.
Формальную аксиоматическую теорию называют полной, если добавление любой невыводимой формулы в качестве схемы аксиом приводит к противоречивой теории.
Исчисление высказываний полно.
