
- •Математическая логика и теория алгоритмов
- •11. Понятие об алгоритмах. Схемы алгоритмов
- •11.1. Понятие об алгоритме и теории алгоритмов
- •11.2. Схемы алгоритмов
- •11.3. Рекурсивные функции
- •11.4. Машина Тьюринга
- •11.5. Машина Поста
- •11.6. Нормальные алгорифмы а.А. Маркова
- •11.7. Универсальная абстрактная машина
- •11.8. Разрешимость в теории алгоритмов. Проблема самоприменимости
- •11.9. Сложность алгоритма
- •11.10. Представление схемы алгоритма эквивалентным автоматом
- •11.11. Представление схемы алгоритма микропрограммой с двумя типами микрокоманд
- •12. Элементы формальной логики
- •12.1. Предмет формальной логики
- •12.2. Понятие и его виды
- •12.3. Отношения между понятиями
- •12.4. Операции над понятиями
- •12.5. Суждение и его характеристика
- •Модальные и категорические суждения.
- •Простые категорические суждения.
- •Виды простых категорических суждений.
- •Распределение терминов в простом категорическом суждении.
- •Логический квадрат.
- •13. Умозаключение
- •13.1. Виды умозаключений
- •13.2. Непосредственное умозаключение
- •Умозаключения путем противопоставления предикату.
- •13.3. Опосредованное дедуктивное умозаключение. Фигуры силлогизма
- •Фигуры пкс.
- •Модусы пкс.
- •13.4. Дополнительные виды силлогизмов
- •13.5. Индуктивные умозаключения. Математическая индукция
- •14. Логика высказываний
- •14.1. Семантика логики высказываний
- •I закон – тождества.
- •14.3. Формализация высказываний
- •14.4. Интерпретации, разрешимость, выполнимость, общезначимость
- •14. 5. Логическая равносильность. Законы логики
- •14.6. Формы представления формул логики высказываний
- •14.7. Проблема дедукции в логике высказываний
- •15. Проверка правильности логических выводов. Метод резолюций
- •15.1. Закон контрапозиции
- •15.2. Логическое следование. Проверка правильности логических выводов
- •15.3. Силлогизмы в логике высказываний
- •Разделительно-категоричные силлогизмы.
- •16. Синтаксис и семантика языка логики предикатов
- •16.1. Понятие предиката
- •16.2. Кванторы и связанные переменные
- •16.3. Синтаксис языка логики предикатов. Формулы логики предикатов и формализация суждений
- •16.4. Семантика формул логики предикатов
- •Общезначимость, выполнимость, невыполнимость.
- •17. Тождественные преобразования формул логики предикатов
- •17.1. Операции над предикатами
- •17.2. Основные равносильности логики предикатов
- •Отрицание предложений с кванторами.
- •17.3. Тождественные преобразования формул
- •17.4. Универсум Эрбрана
- •18. Использование метода резолюций в логике предикатов
- •18.1. Подстановка и унификация
- •18.2. Резольвенция и факторизация
- •18.3. Метод резолюций в логике предикатов
- •18.4. Принцип логического программирования
- •19. Логические исчисления
- •19.1. Понятие о формальных теориях
- •19.2. Исчисление высказываний
- •19.3. Исчисление предикатов
- •19.4. Система натурного вывода
- •19.5. Понятие о математической лингвистике
- •19.6. Формальный язык
- •19.7. Формальные грамматики и их свойства
- •19.8. Теоремы Гёделя
- •20. Неклассические логики
- •20.1. Современные модальные логики
- •20.2. Понятие о теории неопределенности
- •20.3. Элементы теории нечетких множеств и нечеткая логика
- •20.4. Нечеткие алгоритмы
- •Литература
- •Приложение 1 Варианты контрольных заданий по дисциплине «Дискретная математика»
- •Приложение 2 Варианты контрольных заданий по дисциплине «Математическая логика»
19.3. Исчисление предикатов
В логике предикатов, в отличие от логики высказываний, нет эффективного способа распознавания общезначимости формул. Поэтому аксиоматический метод становится главным [19, 26].
Алфавит и определение формулы исчисления предикатов совпадают с логикой предикатов, за исключением того, что в качестве логических операций используем только операции , – .
Аксиомы исчисления предикатов: в качестве трех первых берутся, например, аксиомы исчисления высказываний:
А1. А(ВА);
А2. (А(ВС))((АВ)(АС));
![]()
Добавляются «собственные» аксиомы:
А4. xiA(xi)A(xj), где формула A(xi) не содержит переменной xj.
А5. A(xi)xjA(xj), где формула A(xi) не содержит переменной xj.
Как и ранее А1-А5 – тождественно истинные (общезначимые) формулы.
Действительно, А1-А3 тождественно истинны ( метадоказательство мы приводили выше). А4: xiA(xi)A(xj) – замкнутая формула и ее частный случай xiA(xi)A(xi) при подстановке {(xi,xj)}, что тождественно истинно.
А5:
A(xi)xjA(xj)
может быть представлена в виде
![]() =
=![]() ,
где а – функция Сколема. Частный случай
этой формулы тождественно истинен:
,
где а – функция Сколема. Частный случай
этой формулы тождественно истинен:![]() .
.
Правила вывода.
1.
Правило m.p:
![]() .
Нами уже использовалось и доказывалось.
.
Нами уже использовалось и доказывалось.
2. Правило связывания квантором общности:
![]() ,
,
где
формула В не содержит переменной xi.
Воспользуемся «метадоказательством»:
соответствующее множество дизъюнктов
![]() невыполнимо (а – функция Сколема).
невыполнимо (а – функция Сколема).
3. Правило связывания квантором существования:
![]() ,
,
где формула В не содержит переменной xi.
Метадоказательство:
множество дизъюнктов
![]() также невыполнимо.
также невыполнимо.
4. Правило переименования связанной переменной.
Связанную переменную формулы А можно заменить (в кванторе и во всех вхождениях в области действия квантора) другой переменной, не являющейся свободной в А.
Докажем общезначимость формулы, описывающей правило перестановки разноименных кванторов [24]:
xyP(x,y)yxP(x,y).
1.
![]() yP(x,y)P(x,z)
– по аксиоме 4.
yP(x,y)P(x,z)
– по аксиоме 4.
2.
![]() P(x,z)wP(w,z)
– по аксиоме 5.
P(x,z)wP(w,z)
– по аксиоме 5.
3. (АВ,ВС)(АС) – цепное заключение, которое доказывалось в логике высказываний:
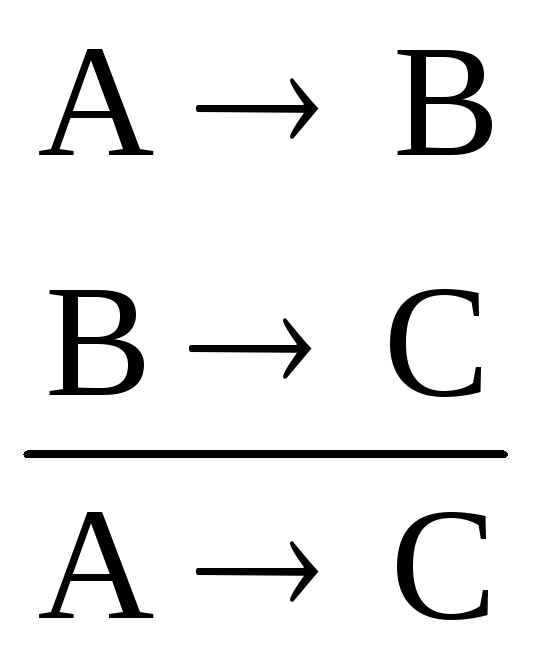 ;
;
![]()
![]()
4.
![]() yP(x,y)wP(w,z),
где 3 применено к 1 и к 2.
yP(x,y)wP(w,z),
где 3 применено к 1 и к 2.
5.
![]() xyP(x,y)wP(w,z)
– по правилу вывода 3 из 4 – связывание
квантором существования.
xyP(x,y)wP(w,z)
– по правилу вывода 3 из 4 – связывание
квантором существования.
6.
![]() xyP(x,y)zwP(w,z)
– правило вывода 2 из 5 – связывание
квантором общности.
xyP(x,y)zwP(w,z)
– правило вывода 2 из 5 – связывание
квантором общности.
7.
![]() xyP(x,y)ywP(w,y)
– правило вывода 4 из 6: переименование
z
в y.
xyP(x,y)ywP(w,y)
– правило вывода 4 из 6: переименование
z
в y.
8.
![]() xyP(x,y)yxP(x,y)
– правило вывода 4 из 7: переименование
w
в x.
xyP(x,y)yxP(x,y)
– правило вывода 4 из 7: переименование
w
в x.
Поскольку в качестве исходных формул использованы только аксиомы, то [xyP(x,y)yxP(x,y)].
19.4. Система натурного вывода
Система натурного вывода – это доказательство в смысле Генцена. Название «натурный» или «естественный» говорит о том, что такой тип рассуждений близок к человеческому (естественному) [32]. Правила вывода в этой формальной системе делятся на правила введения и правила исключения логических операций.
Рассмотрим основные правила введения (В):
введение конъюнкции: (В)
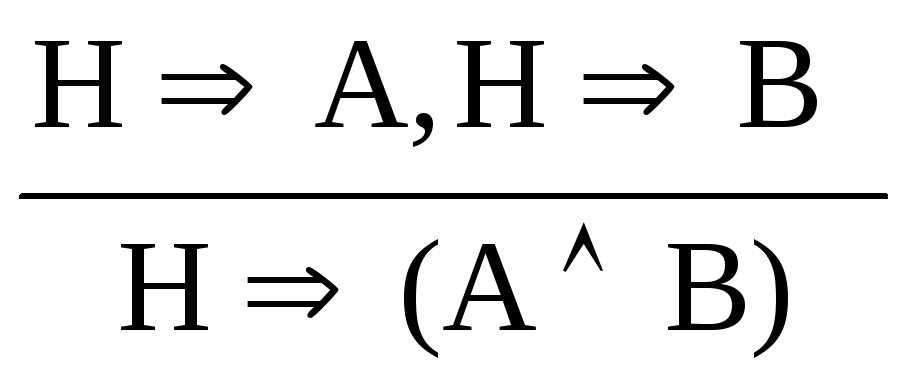 ,
здесь Н – некоторое множество формул
(гипотез);
– метасимвол «влечет», «выводится».
Читается так: «Если из Н выводится А и
из Н выводится В, то из Н выводится
конъюнкция А,В»;
,
здесь Н – некоторое множество формул
(гипотез);
– метасимвол «влечет», «выводится».
Читается так: «Если из Н выводится А и
из Н выводится В, то из Н выводится
конъюнкция А,В»;введение дизъюнкции: (В)
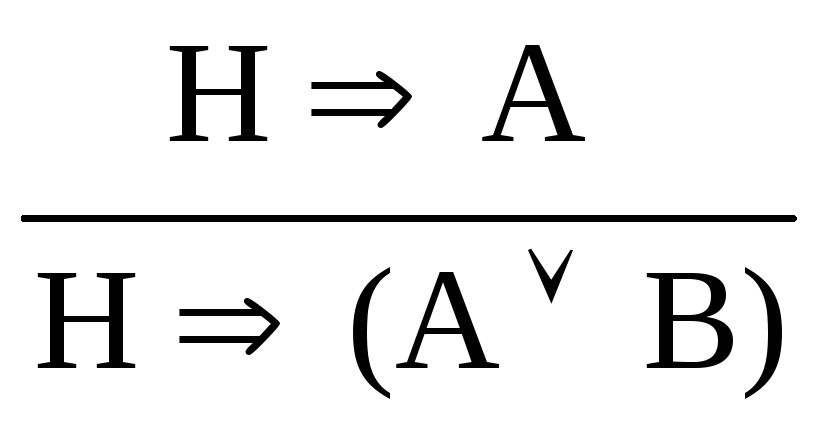 ,
,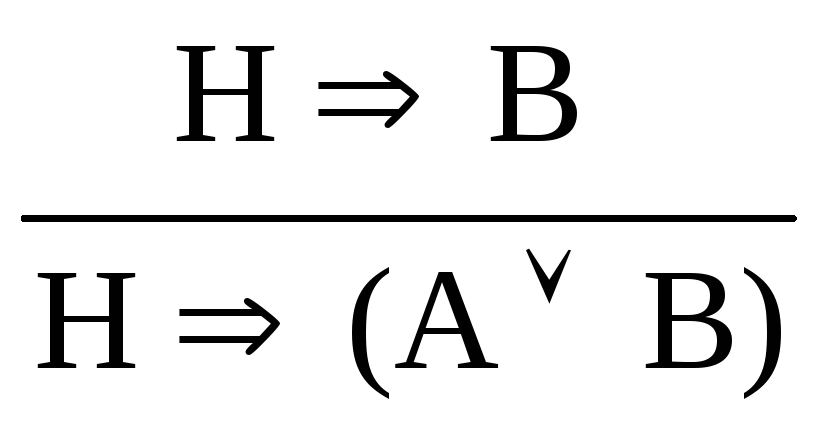 ;
;введение импликации: (В)
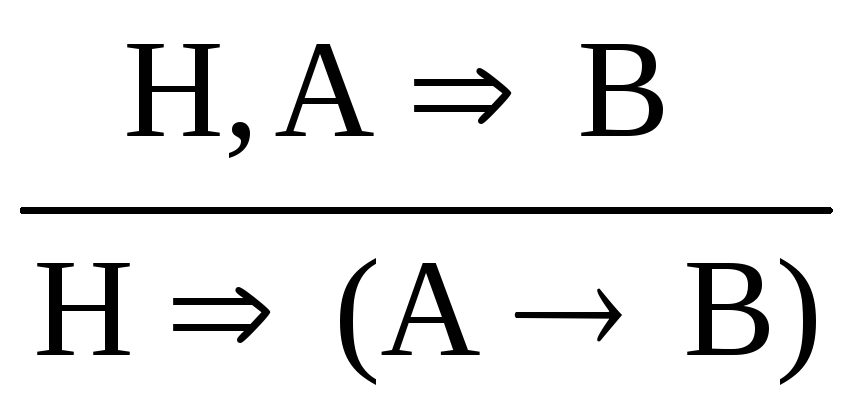 ;
;введение инверсии: (В¯)
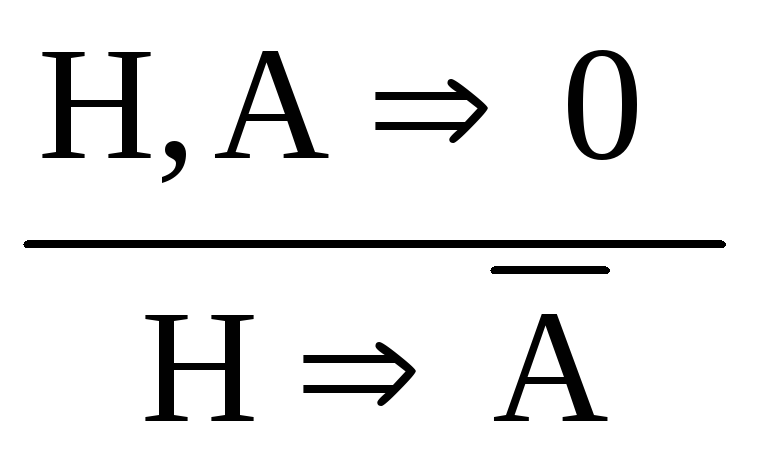 .
.
Рассмотрим основные правила исключения (И):
исключение конъюнкции: (И)
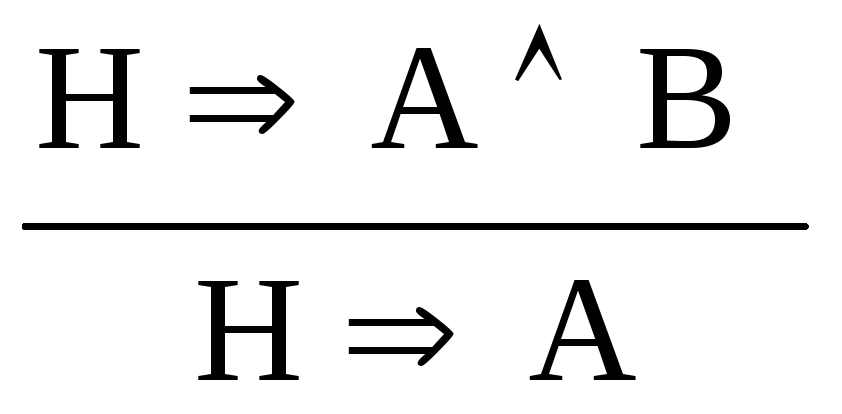 ,
,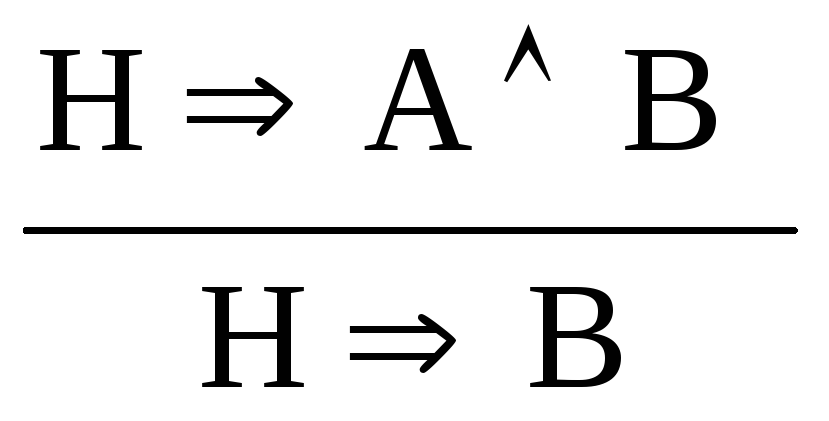 ;
;исключение дизъюнкции: (И)
 ;
;исключение импликации: (И)
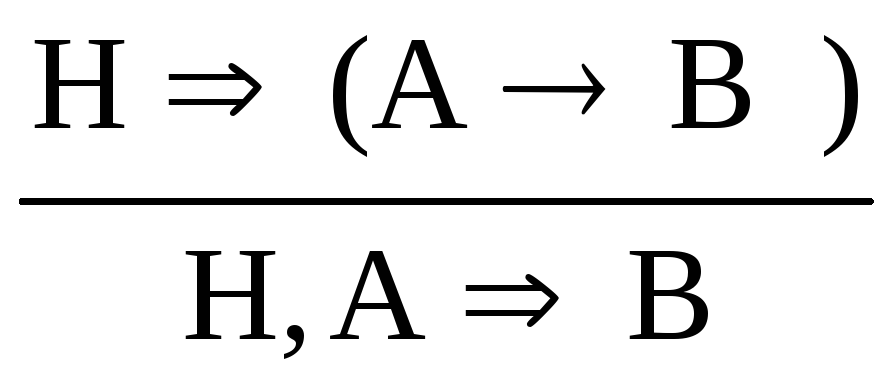 ;
;исключение инверсии: (И¯)
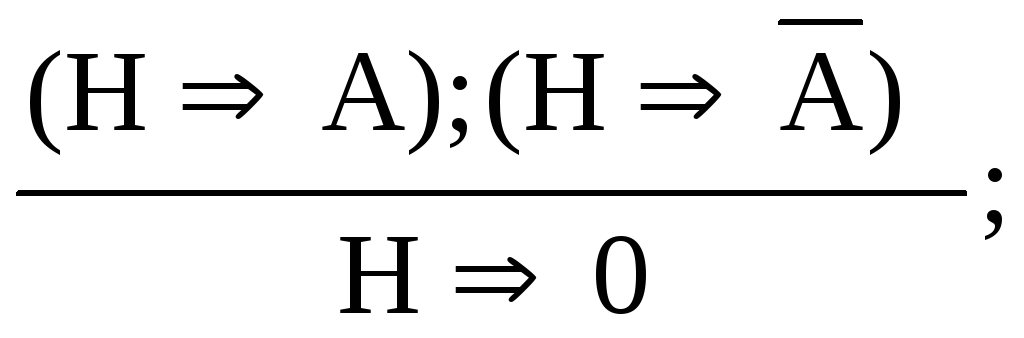
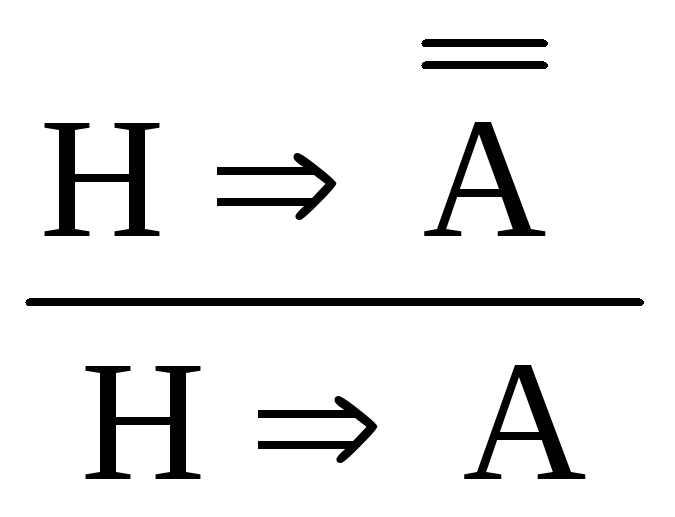 .
.
Кроме того, необходимы еще так называемые базисные правила:
(Б1):![]() ;
(Б2):
;
(Б2):![]() .
.
Первое
базисное правило (Б1) означает, что всякий
вывод, заключение которого совпадает
с одной из гипотез (А) общезначим, то
есть
![]() так
как над чертой нет гипотез (пустое
множество гипотез).
так
как над чертой нет гипотез (пустое
множество гипотез).
Второе базисное правило (Б2) означает, что добавление гипотезы (В) к множеству гипотез не изменяет выводимости.
Рассмотрим пример [32].
Пусть имеется множество формул Н:
{F,F(PQ),PC,QC}=H.
Докажем, что из этого множества выводится формула С.
1) [Н,F(PQ)][F(PQ)]]: правило Б1 – гипотеза [F(PQ)] выводима;
2) Н[F(PQ)]: объединение Н и F(PQ)] это Н;
3) Н,F(PQ)]: в соответствии с 2) и правилом исключения импликации (И): консеквент импликации выводи́м;
4) Н(PQ): объединение Н и F – это Н: т.к. из F выводится (PQ), то и из H тоже выводится (PQ);
5) (Н,PC)(РC): правило Б1 – гипотеза (РC): выводима;
6) Н(РC): объединение Н и (РC) это Н;
7) Н,РC: в соответствии с 6) и правилом исключения импликации (И): консеквент импликации выводи́м;
8) (Н,QC)(QC): правило Б1 – гипотеза (QC): выводима;
9) Н(QC): объединение Н и (QC) это Н;
10) Н,QC: в соответствии с 9) и правилом исключения импликации (И): консеквент импликации выводи́м;
11) НC: в соответствии с 4), 7), 10) и правилом исключения дизъюнкции (И). Таким образом, мы доказали правило «разбора случаев».
