20.2. Понятие о теории неопределенности

Теория неопределенности возникла в связи с решением практических вопросов принятия решений в условиях неопределенности. В последнее время все больше ученых склоняются к тому, что неопределенность – фундаментальный принцип, который следует принимать за аксиому.

Мы знаем математические неопределенности типа: Теорией неопределенности в математическом смысле занимался еще легендарный Э. Галуа.

Физическая неопределенность, например, это неопределенность параметров электрона. В соответствии с принципом неопределенности В. Гейзенберга, чем точнее определяется импульс электрона, тем больше погрешность в координате и наоборот: электрон в одно и то же время и волна, и частица.

Неопределенность связана и с философским понятием свободы выбора. Если все предопределено, детерминировано, то где свобода выбора? В православии примером свободы выбора является, например, выбор Адама в Эдеме, предоставленный ему Создателем.

Имеется два основных типа неопределенности:

1) вероятностная или стохастическая;

2) лингвистическая.

Первая обусловлена случайными факторами – отказами производственного оборудования, перебоями с поставками комплектующих изделий и сырья, случайностью поведения конкурента и т.д.

Вероятностная неопределенность формализуется теорией вероятности, математической статистикой, теорией массового обслуживания.

Вторая связана с нечеткостью (расплывчатостью) целей и (или) ограничений. Она формализуется теорией нечетких множеств, нечеткой логикой и нечеткими алгоритмами. Эти методы сегодня широко применяются в экономике для учета различных рисков.

20.3. Элементы теории нечетких множеств и нечеткая логика

Нечёткая логика («fuzzy logic», расплывчатая, размытая, «пушистая логика») использует лингвистическую неопределенность и основана на теории нечетких множеств [29]. Впервые была предложена профессором компьютерных наук университета г. Беркли (США) Л. Заде в середине 60-х годов ХХ века. Обычное «четкое» множество имеет четкие границы в некотором универсуме. Принадлежность элемента универсума к некоторому множеству оценивается бинарно: «Да» или «Нет». Такая принадлежность элемента х к множеству А на универсуме U может быть описана так называемой функцией принадлежности _А:

А={(х, _А(х))},хU, _А(х){0,1}.

Здесь А задано как совокупность пар – «элемент-степень принадлежности к множеству». То есть для обычного множества _А это отображение элементов универсума U в бинарное множество {0,1}:_А:U{0,1}.

Нечёткое множество А в универсуме (пространстве) U задается функцией принадлежности, отображающей универсум не в бинарное множество, а в интервал [0,1]. Тогда задание нечеткого множества выглядит так:

А={(х,_А(х))},хU,_А(х)[0,1],_А:U[0,1].

То есть, степень принадлежности элемента к множеству оценивается не скачком «либо 0, либо 1», а плавно, например: 0;0,1;0,4;0,7;0,9;1. Функция принадлежности может задаваться формулой, графически – например так, как указано на рис. 128.

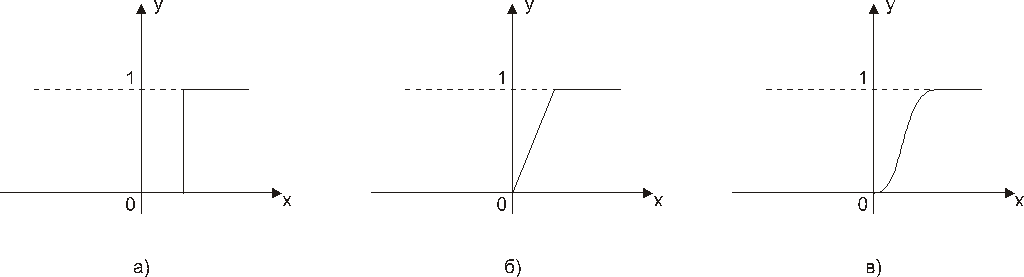
Рис. 128. Функции принадлежности

а) дискретная, б) плавная-кусочно-линейная, в) сигмоида

В случае конечного обозримого множества применяют следующую запись [41]:

.

Это означает, что:

• элемент 1 принадлежит к универсуму U со степенью 0, т.е. не принадлежит;

• элемент 2 принадлежит к универсуму U со степенью 0,1;

• элемент 3 принадлежит к универсуму U со степенью 0,3;

• элемент 4 принадлежит к универсуму U со степенью 0,5;

• элемент 5 принадлежит к универсуму U со степенью 0,8.

Знак + означает объединение элементов. Сам универсум U=1+2+3+4+5.

Множество пусто, если xU _А(х)=0, т.е. А=.

Если xU _А(х)=1, то А=U.

Два множества А и В равны, если _А=_В, т.е. А=В.

Множество А включается в В, если _А_В т.е. АВ.

Множество A есть дополнение множества А, если .

Вводятся также двухместные теоретико-множественные операции:

Пересечение множеств А и В:

АВ=_АВ = min{_А;_В }.

Пример.

;

.

Объединение множеств

АВ=_АВ=max{_А;_В}.

Пример.

;

.

Этим операциям соответствуют нечеткие конъюнкция и дизъюнкция в нечеткой логике, где А и В – элементарные нечеткие высказывания, а АВ – нечеткое составное высказывание «А или В», АВ нечеткое составное высказывание «А и В». Тогда U – область рассуждения.

Импликация в том виде, который используется в классической логике, не применяется.

Чаще всего используют импликацию в виде: «Если А, то В, иначе С», при этом такое высказывание определяют через нечеткое отношение на декартовом произведении множеств, то есть . При этом Х – область рассуждения для высказывания А,Y – область рассуждения для высказывания В, и в общем случае они разные. Если С не указано и универсум Y области рассуждения для высказывания В, то получаем )[41]. При этом функция принадлежности пары определяется как минимум функций принадлежности элементов пары.

Пусть Х=1+2; Y=1+2; ;.

Тогда Или в виде табл. 97:

Таблица 97

Декартово произведение нечетких множеств А и В

		В
		1	2
А	1	0,5	1
	2	0,5	0,7

Получим .

Тогда Или в виде табл. 98:

Таблица 98

Декартово произведение нечетких множеств A и Y

		Y
		1	2
	1	0	0
	2	0,3	0,3

Очевидно, что универсум

В таком случае

То есть в данном случае получили .

В теории нечетких множеств также вводится операция концентрации: Con(А) – возводит функцию принадлежности в квадрат.

Деконцентрация (растяжение) Dil(А) – извлекает квадратный корень из функции принадлежности.

Пример.

А=;Con(А)=;

B=;Dil(В)=.

Например, если А – «маленький», то Con(А)=«очень маленький». Если В «хороший», то Dil(В)=«более или менее хороший».

Вводятся также и алгебраические операции над нечеткими множествами:

1) алгебраическое произведение: ;

2) алгебраическая сумма: .

Рассмотрим пример применения нечеткой логики. Пусть нечеткие множества заданы графически на числовой (денежной) оси.

Пусть П – нечеткое подмножество универсума Х «Прибыль», З – нечеткое подмножество универсума У «Зарплата». Рассмотрим три подмножества прибыли – малая (М_п), средняя (С_п), высокая (В_п); три нечетких подмножества зарплаты – малая (М_з), средняя (С_з), высокая (В_з) (рис. 129).

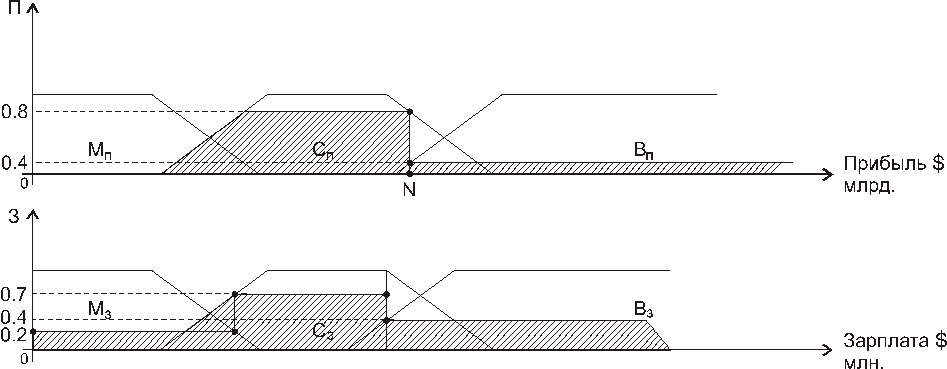
Рис. 129. П – нечеткие подмножества прибыли;

З – нечеткие подмножества зарплаты

Пусть дано нечеткое высказывание «Какая прибыль, такая и зарплата». Очевидно, что это не одно и то же с высказыванием «Какая зарплата, такая и прибыль». В отличие от «четкой» логики, где имеет место высказывание «Прибыль тогда и только тогда, когда зарплата» (эквиваленция ПЗ), задается матрица нечеткого отношения R на декартовом произведении соответствующих множеств П, З: ПЗ=R. Получим табл. 99. В ней степени принадлежности выбраны, например, путем опроса специалистов – экспертов.

Таблица 99

Матрица нечеткого отношения

«Какая прибыль, такая и зарплата»

	МЗ	СЗ	ВЗ
МП	0.7	0.2	0
СП	0.2	0.7	0
ВП	0	0.2	0.7

Пусть предприятием получена некоторая прибыль точка N на оси прибыли (рис. 129), которая может быть представлена выражением:

.

Мы провели фаззификацию – по конкретному значению прибыли N получили нечеткое множество П, показанное на рис. 129 штриховкой по оси прибыли.

Спрашивается, какая будет зарплата? Зарплата З определяется как произведение нечеткого множества П на матрицу отношения R:

Полученный результат графически (штриховкой) представлен на рис. 129 (ось З). Это нечеткая зарплата, нечеткое множество З. Но мы хотим четкую зарплату! Поэтому проводят так называемую дефаззификацию, т.е. получение четкого значения параметра. Одним из способов дефаззификации является определение «центра тяжести» нечеткого множества (показанного на рис. 129 штриховкой). Таким образом, получаем довольно неплохую зарплату.