Geofizichna_gidrodinamika_statsionar

Знайти залежності між фізичними величинами з використанням П–теореми

1. Розглянемо опір повітря руху твердих тел. Візьмемо випадок обігу руху. Хай газоподібне середовище обтікає нерухоме тіло. Сила опори визначається наступними параметрами – густина, – швидкість,

s - поперечний переріз тіла і безрозмірним коефіцієнтом опору. Сформувати, використовуючи П–теорему, безрозмірний комплекс, який називається критерієм Ньютона.

2.Розглянемо рух в’язкої рідини. До числа характерних параметрів відносяться V , l – лінійний розмір, – динамічний коефіцієнт в’язкості і

. Знайти безрозмірний комплекс.

3.Число Річардсона є характеристикою турбулентності потоку за наявності температурної неоднорідності, тобто чинниками, від яких залежить число Річардсона, є чинники, що визначають розвиток

турбулентності: Vz – вертикальний градієнт швидкості потоку, –

густина рідини, z – вертикальний градієнт густини, g – сила тяжіння.

Виходячи з міркувань розмірності, знайдіть вираз числа Річардсона. 4. В ідеальному газі тиск є функцією густини, температури і питомих

теплоємностей Cp та CV . Вивести формулу, яка надає відповідну

залежність. Вказівка: необхідно використати поняття симплексу.

5. Рідина і стан руху рідини в цілому визначаються системою

параметрів:	p1	p2	– перепад тиску уздовж відстані l , а p	і p – тиск в
		l	1	2

перетинах труби, віддалених один від одного на відстані l ; густина; перетин труби; середня швидкість рідини по перетину труби. Утворити з цих величин безрозмірну комбінацію, яка називається коефіцієнтом опору труби.

6. Математичний маятник є важкою матеріальною точкою, яка є підвішена на невагомій і нерозтяжній нитці, яка була закріплена іншим своїм кінцем нерухомо. Силами опору нехтуємо. Рухи маятника плоскі. До визначальних параметрів в даному випадку відносяться: l – довжина маятника, 0 – кут між ниткою і вертикаллю в початковий момент часу,

t – час, m – маса вантажу, g – прискорення вільного падіння.

Враховуючи, що одним з незалежних безрозмірних параметрів, що характеризує рух маятника, є 0 , складіть другу безрозмірну комбінацію.

7. Маємо такі змінні і їх розмірності: z – висота, g – параметр плавучості, KTE – кінетична енергія турбулентного руху, віднесена до

113

2 2

одиниці

),

zi

–

маси ( L T

– потужність шару перемішування, w

кінематичний потік тепла в напрямку вісі z ( LT 1K ).

Сформуйте,

використовуючи П–теорему, безрозмірні

комплекси,

узявши KTE , zi і

в якості незалежних величин.

w

може бути

8. В

найзагальнішому

випадку

шорсткість поверхні

представлена залежністю

z0 f *, g, ,t, x, , ,

де

*

– динамічна

швидкість (LT-1), g – прискорення

вільного падіння,

- кінематичний

коефіцієнт в’язкості води, t

– час з початку дії вітру,

x – розгін хвилі,

і

– густина повітря і

води відповідно. Звести

дану залежність

до

функціонального зв’язку між безрозмірними комплексами. Отримати вираз для z0 у разі сталого розвиненого хвилювання в горизонтально–

однорідних умовах, нехтуючи силами в’язкості.

9. Розглянемо питання про коливання конструкції за відсутності демпфуючих сил. В цьому випадку, окрім зовнішніх сил, діють сили інерції і пружності, причому останні грають роль поновлюючих сил.

Враховуючи, що інерційні сили залежать від добутку ddt , а поновлюючи сили від модуля пружності E (Н·м-2) природно виділити як характерні параметри: 0 – безрозмірний коефіцієнт Пуассона, E , , ddt , l – зсув

відносно точки рівноваги, F – початково прикладена сила. Звести дану залежність до функціонального зв’язку між безрозмірними комплексами.

10. Розглядається ідеалізований випадок витікання сипучого матеріалу з отвору, тобто, будемо вважати, що злипання частинок та внутрішнє тертя є відсутнім. Тоді параметрами процесу є: Q – витрата

сипучого матеріалу (тобто маса матеріалу, яка проходить крізь отвір за одиницю часу); D – діаметр отвору; d – середній розмір зерна; –

густина; g – прискорення вільного падіння. Знайти безрозмірні комплекси та встановити зв’язок між ними.

5.2 Теорія подібності

Позначимо словом система сукупність фізичних об’єктів (елементів системи), що об’єднуються на основі деякої ознаки, що індивідуалізує набір даних елементів та надає системі певні якості. На увазі будемо мати такі системи, стан яких є однозначною функцією стану окремих елементів. Деякі приклади систем: літак, маятник, тощо.

Параметрами системи назвемо величини, які характеризують її елементи та об’єкти, що впливають на систему, тобто величини, які вирізняють кожен об’єкт з множини інших тієї ж самої фізичної природи;

114

узагальнені координати системи – це величини, які описують поведінку системи та повністю характеризують її положення – їх кількість дорівнює числу степенів свободи системи.

Узагальнені координати можуть змінюватися з плином часу, або від точки до точки. Наприклад, для системи, в якій вантаж масою m коливається на пружині жорсткістю при прискоренні вільного падіння

g , узагальненою координатою є вертикальний зсув ( x ) вантажу від деякого початкового положення, а основними параметрами m , , g . З

множини параметрів даної системи вирізняють мінімально можливу кількість параметрів, яких досить для однозначного визначення стану системи; ці параметри між собою є незалежними1, назвемо їх основними, або визначальними.

Нехай є дві системи однакової фізичної природи, які складаються з однакового числа аналогічних елементів, які відіграють в обох системах однакову роль. Одну систему назвемо моделлю, іншу систему – натурою, величини, що відносяться до них, позначимо відповідно індексами м та

н .

Система визначається s основними параметрами ( p j ) та має r

незалежних узагальнених координат qi . З метою тотожності час та

початкові умови включимо в число параметрів та умовимося, що індекс i приймає значення 1,2,...,r , а індекс j – значення r 1,...,r s .

Узагальнені координати цих систем є однаковими функціями параметрів:

		qi м f pr 1 м,..., ar s м ,							(5.8)
		qi н f pr 1 н,..., pr s н .							(5.9)
Взагалі, qi	м	qi	н	, p j	н	p j	м	.

Дві системи називають подібними, якщо їх будь–які дві відповідні узагальнені координати для будь–яких схожих моментів часу (схожих точок простору)є пропорціональними, тобто дві системи подібні, якщо

qi tн	н	kq	qi tм	м	,	(5.10)
		i

1 Не плутати з величинами з незалежними розмінностями. Тут термін «незалежні» вживається в сенсі, що обрані величини однозначно визначають процес або явище, проте не дублюють одна одну. Так, наприклад, якщо до числа визначальних параметрів входить густина, то маса вже буде зайвим параметром в цій задачі.

115

де kqi const , tн kttм, tн , tм – схожі моменти часу; kqi називають

масштабним множником або коефіцієнтом подібності.

Таким чином, якщо відомо, що дві системи подібні та можна знайти коефіцієнти подібності kqi , то, знаючи поведінку однієї системи (моделі),

можна знайти і то, як буде поводитись інша система (натура).

Прикладом подібності систем може слугувати один з найбільш простих випадків. Дві механічні системи, для будь–яких точок яких є справедливими рівності

xi tн	н	kl xi tм м,
yi tн н kl yi tм м,			(5.11)
zi tн	н	kl zi tм м,

очевидно, будуть подібними (такі системи називають ще кінематично подібними). В даному випадку узагальненими координатами є декартові,

коефіцієнти подібності для всіх координат однакові.
Якщо між точками			систем існує ще матеріальна	подібність,	тобто
	mi н	km const ,	то системи називають динамічно	подібними.	При
	mi м

наявності динамічної подібності дуже легко встановлюється зв’язок між всіма кінематичними та динамічними характеристиками систем. Так, для швидкостей є характерним зв’язок:

ui	н		d xi	н	dtн		k
						k	l ,
ui м			d xi м		dtм	u	kt

аналогічно можна отримати вирази для інших складових швидкості.

для прискорень:

ai	н				k
		k			l	,
ai			a		kt2
	м

для сил:

(5.12)

(5.13)

Fi	н		a m		k		k
			н н	kmka		m	l	k f ,	(5.14)
Fi
	м		aмmм		kt2

116

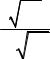
для роботи:

Ai

н

F l

k

k2

н н

k

k

m l

k

,

Ai

f

l

A

м Fмlм

kt2

для потужності:

kN kmkl2 , kt3

для сил та потужності:

kN kl kkf ,

(5.15)

(5.16)

(5.17)

тощо.

Можна помітити, що при динамічній подібності систем коефіцієнти подібності різних величин представляються через коефіцієнти подібності km , kl , kt – за допомогою формули розмірності цих величин:

k	f	kmkl ; F MLT 2	, k	kl		; F LT 1 .	(5.18)
		kt2	u		kt

5.2.1 Необхідні та достатні умови подібності

Теорема. Достатньою умовою подібності двох систем є рівність будь–яких відповідних критеріїв подібності цих систем, знайдених з їх основних параметрів та початкових (граничних) умов за допомогою –

теореми.

Тобто, якщо узагальнені координати та основні параметри зв’язано деякою функціональною залежністю, вигляд якої у загальному випадку є невідомим:

qi f pr 1,..., pr s ,

(5.19)

то зведена функціональна залежність матиме вигляд

i r 1,..., r s k ,

(5.20)

117

де i		,		r 1		,		r s k		. Цю
		qi				pr 1				pr s k
	p1 i pk i				p1 r 1 pk r 1				p1 r s k pk r s k

залежність можна отримати за допомогою –теореми, надасть r s k

критеріїв подібності, де k – у загальному випадку є кількістю основних одиниць вимірювання, що використовуються в задачі. Тобто замість r первинних співвідношень (5.19) отримано r співвідношень (5.20) між

s k безрозмірними комплексами.

Аналогічно, (5.8) та (5.9) можна привести до виду:

i м	r 1 м , , r s k м ;	(5.21)
i н	r 1 н , , r s k н .	(5.22)

Якщо нові параметри – безрозмірні комбінації величин – однакові в обох функціях в (5.21) та (5.22), то, очевидно, ліві частини рівностей (5.21) та (5.22) також однакові:

i м i н , i 1,2,...,r .

(5.23)

Отже, щоб явище, що імітується, буле подібне до моделі, потрібно:

1)вибрати s визначальних параметрів, включаючи до них початкові (граничні) умови та, якщо необхідно, час, та здобути з них s k незалежних критеріїв подібності;

2)вибрати параметри натури так, щоб її критерії були такі самі, як і у моделі;

i м i н , i 1,2,..., s k .

(5.24)

Причому умову i м i н прийнято записувати, як i idem , деidem латинською означає такий самий, одне й те саме.

Теорема. Необхідною умовою подібності двох систем є рівність відповідних критеріїв подібності цих систем, що здобуті на підставі узагальнених координат та параметрів систем.

Якщо достатні умови накладають певні обмеження на параметри систем, обумовлюючи цим їх подібність, то необхідні умови дозволяють встановити зв’язок між координатами та параметрами систем, якщо вони є подібними.

118

5.2.2Рекомендації по вивченню теми

В теорії подібності викладено принципи, які дозволяють побудувати фізичну модель (тобто матеріальне втілення) досліджуваного явища. В багатьох випадках побудова моделі набагато полегшує дослідження натури (природного явища), бо часто, на відміну від моделі, проводити експерименти саме з природним явищем (натурою) важко або неможливо. Теорія подібності досліджує умови, за яких модель можна вважати відповідною до натури, та дозволяє визначити критерії подібності, за допомогою яких можна перерахувати визначальні параметри з моделі на натуру та навпаки.

Під час вивчення цієї теми студент повинен звернути увагу на наступні знання та вміння:

поняття «параметр системи» та «узагальнені координати»; необхідні та достатні умови подібності двох систем;

визначення та методи знаходження критеріїв подібності, у випадку, якщо надано визначальні параметри системи, та у випадку, якщо надано математичний опис явища у вигляді диференціальних рівнянь.

Більш детальну інформацію з цієї теми студент може отримати в конспекті лекцій [6] – стор. 42–57.

5.2.3Приклади розв’язання типових задач

Задача № 1.

Умова. Відомими величинами є масштабні множники подібності мас km 0.9 , робітkA 1.92 та потужностей kN 1.48 . Знайти масштабні

множники геометричної та часової подібності та масштабний множник подібності сил.

Розв’язання задачі.

З теорії відомо, що коефіцієнти подібності одних фізичних величин можна виразити через коефіцієнти подібності інших фізичних величин, скористувавшись математичним записом закону, через який ці фізичні величини пов’язані. Виразом через які пов’язані потужність та робота є

N dA , тобто k

N

kA ,

звідси k

kA

.

dt

kt

t

kN

1.92

Тоді

k

1.3, використовуючи значення k

m

та формули (5.16)

t

1.48

і (5.17), знайдемо:

k3

1.3 3

k

1.92

k

k

t

1.48

1.9

і k

f

A

1.01.

N k

0.9

1.9

l

m

k

l

119

Задача №.2.

Умова. Обчислити розміри, вагову водотоннажність судна в морській

воді (густина морської води = 1.025 т/м3)		і змочену поверхню судна,
геометрично подібного моделі, що має наступні			головні	вимірювання:
довжина Lм 2 м, ширина	Bм 0.4 м,	висота	борту	H м 0.18 м і

осідання судна Tм 0.1 м. Водотоннажність моделі в прісній воді складає

0.007 т, змочена поверхня моделі при заданому осіданні Sм 1.2 м2 . Коефіцієнт геометричної подібності при моделюванні дорівнює 50.

Розв’язання задачі.

Знаючи лінійні розміри моделі і коефіцієнт геометричної подібності ми можемо отримати аналогічні лінійні розміри судна.

Звідси:

довжина судну: Lн k Lм 50 2 м 100 м; ширина судну: Bн kBBн 50 0.4 м 20 м;

висота борту: Hн kH H м 50 0.18 м 9 м; осідання судну: Tн kTTм 50 0.1м 5 м.

Для того щоб перерахувати характеристики, що отримані для моделі, з моделі на судно, необхідно одержати коефіцієнти подібності для цих характеристик.

Для змоченої поверхні судна цей коефіцієнт дорівнюватиме kS kL 2 , тобто Sн ksSм 2500 1.2 м2 3000 м2 .

Водотоннажність судна ( mн) ми можемо знайти, знаючи об’єм

витисненої води (Vвн ) та її густину mн мвVвн. Об’єм води, що витиснена моделлю, (позначимо його через Vвм) можна отримати, якщо поділити водотоннажність моделі на густину прісної води (випробування моделі

проводились саме в такій воді): V м						mM	0.007 т	0.007м3 ,	де	пв	–
					в	пв	1т/ м3
густина			прісної води.		Коефіцієнт подібності для			об’єму знайдемо як
k	k		3 .	Звідси ми можемо отримати об’єм витисненої судном води
V
V н	k V м			125000 0.007 м3 875 м3
в	V		в
	Таким			чином	водотоннажність			судна	дорівнює
m			V н 1.025т/ м3 875м3 897т.
н		мв в

120

Задача № 3.

Умова. Розглянемо способи отримання критеріїв подібності на прикладі вимушених механічних коливань з демпфуванням (демпфування коливань – штучне придушення коливань механічної, електричної та інших систем). Вантаж масою m коливається на пружині жорсткості у

в’язкому середовищі, сила опору F k , де k – коефіцієнт пропорційності та – швидкість системи. На вантаж діє збурювальна сила

F sin t , де	2	– циклічна частота, а t – час.
0	T

Розв’язання задачі.

Переміщення вантажу x , тобто узагальнена координата у цьому випадку, є функцією цих величин та часу:

x f m,k, , F0, ,t .

Будемо шукати розв’язання цієї задачі у системі LMT . Число степенів свободи системи дорівнює одиниці, тому для однозначного визначення положення системи необхідна лише одна узагальнена координата, x , тобто r 1. Кількість основних параметрів ( s ) дорівнює 6. кількість параметрів з

незалежними розмірностями: k 3 , тому усього можна здобути s r k ,

тобто 4 критерію подібності. Прийнявши за величини з незалежними розмінностями t , m , x , представимо критерії подібності у наступному вигляді:

kt2

t

F t2

;

2

;

3

0

;

4

t .

1

m

m

xm

Функціональну залежність можна представити у вигляді:

	F					, або	kt2		t		F t2
		2	,	,	4			F		,	0	, t .
							m				xm
1			3					m

При фізичному моделюванні дві системи – модель і натура – є подібними, якщо

kt2

t

F t2

idem ;

2

idem ;

3

0

idem ;

4

t idem ,

1

m

m

xm

121

або

k

t2

k t2

t

t

F t2

F t2

м м

н н ;

м

м

н

н ;

0м м

0н н

;

t

м

t

н

. (*)

mм

mн

mм

mн xмmм xнmн

м

н

Рівність критеріїв подібності (*) є необхідною умовою подібності. Для того, щоб сформулювати достатні умови подібності треба мати початкові умови.

Якщо розглядати сталий рух, то з числа визначальних параметрів вилучається час (t ). Тоді залежність набирає наступного вигляду:

x f m,k, , F0, ,t , r 1, s 5, k 3 ,

а кількість критеріїв подібності 3. Обравши за величини з незалежними

розмірностями x , ,

m та провівши всі необхідні алгебраїчні операції,

матимемо:

F0

,

,

k

.

xm 2

m

m 2

Функціональну залежність представимо наступним чином:

F

k

0

F

,

.

xm 2

m 2

m

Критерії подібності матимуть наступний вигляд:

F

2

k

1

0

idem ; 2

idem ;

3

idem ,

xm 2

m

m 2

або

F

2

F

2

м

н

k

м

k

н

0м

0н

;

;

.

x

м

m

2

x m 2

mм м

mн н

m

2

m 2

м

м

н н

н

м

м

н н

Якщо фізичну задачу сформульовано математично, то отримати критерії подібності можна безпосередньо з рівняння, що описує фізичне явище. Розглянемо попередню задачу, записавши диференційне рівняння вимушених коливань з демпфуванням:

122