
Geofizichna_gidrodinamika_statsionar
.pdf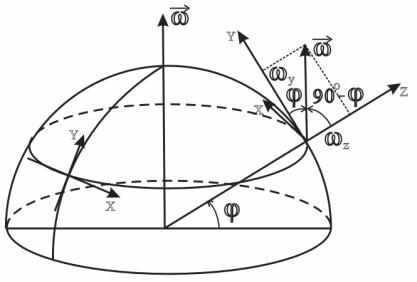
|
|
i |
j |
k |
|
|
|
|
x yu . |
|
|
||||||||
V |
|
x |
y |
z |
|
i |
yw z j |
zu xw k |
|
|
|
u |
|
w |
|
|
|
|
|
Щоб отримати остаточний вираз для складових сили Коріоліса необхідно знайти, як виражаються проекції x , y та z (рис. 3.8).
Рисунок 3.8. – До знаходження складових сили Коріоліса
З рис. 3.8 |
видно, що вектор кутової швидкості Землі знаходиться в |
|||||
площині YOZ , |
тобто проекція x дорівнює нулю. Кут між вектором та |
|||||
віссю OY дорівнює , а між вектором та віссю OZ – 900 . Тоді, |
||||||
y |
|
cos cos , а |
z |
|
sin 900 sin 900 . Тобто в |
|
|
|
|||||
остаточному вигляді складові сили Коріоліса матимуть вигляд:
Kx 2 yw z 2 w cos sin ;
K y 2 zu xw 2u sin ;
Kz 2 x yu 2u cos .
73
3.2.7Контрольні питання до теми
1.Сформулюйте теорему Коріоліса.
2.Які додаткові прискорення ми повинні враховувати, якщо враховуємо обертання Землі?
3.Чи враховуємо ми прискорення, яке виникає за рахунок зміни кутової швидкості Землі?
4.На які тіла впливає відцентрова сила?
5.Що представляє собою сила тяжіння?
6.Дайте визначення геопотенціалу.
7.Чи впливає сила Коріоліса на нерухомі тіла?
8.Як спрямована сила Коріоліса відносно руху чистинки?
9.Поясніть механізм дії сили в’язкості.
10.Чи може сила внутрішнього тертя виникати в рідинах, що знаходяться в стані спокою?
11.Що є виявами дії сили в’язкості в рідині?
3.2.8Задачі для самостійного розв’язання
1.Розрахувати величину лінійної швидкості, яка створюється твердотільним обертанням Землі на широті 60° північної півкулі.
Прийняти, що радіус Землі дорівнює 6370 км, а кутова швидкість обертання 7,29·10-5 с-1.
2.На якій географічній широті твердотільне обертання Землі
створює лінійну швидкість 402 м/с. Прийняти, що радіус Землі рівний 6370 км, а кутова швидкість обертання 7,29·10-5 с-1.
3.Обчислити проекції вектора кутової швидкості обертання Землі на нормаль до земної поверхні, спрямовану від центру планети, для екватора, 30° північної широти і північного полюса.
4.Частинка одиничної маси на широті 45° північної півкулі
рухається в горизонтальній площині по меридіану на північ із швидкістю 5 м/с. Кутова швидкість обертання Землі рівна 7,29·10-5 1/с. Розрахувати модуль і вказати напрям сили Коріоліса.
5.Використовуючи стандартну систему координат (вісь Ох направлена по паралелі на схід, вісь Оy – по меридіану на північ, вісь Оz –
взеніт) розрахувати складові сили Коріоліса для частинки одиничної маси, що переміщається в горизонтальній площині з південного заходу на
північний схід із швидкістю 10 м/с на широті 30° північної півкулі. Модуль вектора кутової швидкості обертання Землі дорівнює 7,29·10-5 1/с.
6.Використовуючи стандартну систему координат (вісь Ох направлена по паралелі на схід, вісь Оy – по меридіану на північ, вісь Оz –
взеніт) розрахувати складові сили Коріоліса для частинки одиничної маси, що переміщається вертикально вгору із швидкістю 1 см/с на широті 60°
74

північної півкулі. Модуль вектора кутової швидкості обертання Землі дорівнює 7,29·10-5 1/с.
7.Знайти модуль сили Коріоліса, що діє на частинку одиничної маси, яка переміщується перпендикулярно поверхні Землі, тобто вертикально
вгору, із швидкістю 2 см/с на широті 60° північної півкулі. Кутова швидкість обертання Землі 7,29·10-5 с-1.
8.Розрахувати величину швидкості руху частинки одиничної маси,
якщо відомо, що вона рухається на північ на широті 30° північної півкулі, а модуль сили Коріоліса дорівнює 0,218·10-5 м/с2. Прийняти, що кутова швидкість обертання Землі 7,29·10-5 1/с.
9.Визначити абсолютну величину і напрям відцентрової сили для
одиниці маси на широті 60° північної півкулі. Прийняти, що радіус Землі дорівнює 6370 км, а кутова швидкість обертання Землі 7,29·10-5 с-1.
10.Знайти відношення модулів векторів відцентрових сил для частинок одиничної маси, що розташовані на широтах 30° і 60° північної півкулі.
3.3Оператор Гамільтона
Оператор Гамільтона – це векторний оператор, проекціями якого на координатні осі прямокутної декартової системи координат є частинні похідні за відповідними координатами
¶ |
¶ |
¶ |
|
|
||||
= i |
|
+ j |
|
+ k |
|
. |
(3.21) |
|
¶x |
¶y |
¶z |
||||||
|
|
|
|
|
||||
Він являє собою символічний вектор з проекціями ¶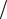 ¶x, ¶
¶x, ¶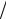 ¶y, ¶
¶y, ¶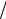 ¶z на
¶z на
координатні осі (у випадку прямокутної декартової системи координат) і називається оператором “набла” (позначається - ).
Оператор Гамільтона дозволяє математично визначити основні диференціальні характеристики векторних та скалярних полів, з якими оперує геофізична гідродинаміка (найчастіше це поля швидкості, тиску та температури). Для зручнішого визначення і подальшого користування оператором “набла” існує поняття “суми за Ейнштейном”, що являє собою скорочену форму запису суми двох або більше однакових за структурою доданків. Найпростіший приклад використання поняття “суми за
Ейнштейном” – скалярний добуток двох довільних векторів a і b :
(a b )= axbx + ayby + azbz = |
|
= a1b1 + a2b2 + a3b3 = aaba , a =1,3 . |
(3.22) |
75
В результаті три однакові за структурою доданки представлено у вигляді одного з індексами a , що повторюються. Отже, присутність в математичному виразі індексу, що повторюється, вказує на наявність “суми за Ейнштейном”. Як правило, поруч вказується, які значення приймає цей індекс (якщо ні – вважається, що він змінюється від 1 до 3 або приймає значення x, y, z ).
Оператор Гамільтона в термінах “суми за Ейнштейном” набуває вигляду
|
¶ |
|
¶ |
|
¶ |
|
¶ |
|
|
|
|
|
|
|
|
||||||||
= i |
|
+ i |
|
+ i |
|
= i |
|
, a =1,3. |
(3.23) |
||
|
|
|
|
||||||||
1 ¶x |
2 ¶x |
3 ¶x |
a ¶x |
|
|
|
|
||||
|
1 |
|
2 |
|
3 |
|
a |
|
|
|
|
Основними диференціальними характеристики векторних та скалярних полів, які дозволяє визначити оператор “набла”, є градієнт, дивергенція та ротор. В застосуванні до задач геофізичної гідродинаміки будемо визначати операцію “градієнт” як векторний оператор над скалярним полем A.
Скалярним полем A(x, y, z)= A(r ) називається скалярна величина A , яка визначена в кожній точці r = (x, y, z) простору (тобто приймає в них
конкретні значення, наприклад, поле температури, густини в неоднорідному середовищі, і т.д.).
Точки простору, в яких функція A = A(r ) приймає одне й те саме значення A(x, y, z)= const , утворюють поверхню рівня.
Градієнтом grad A скалярного поля A = A(r ) називається вектор,
визначений в кожній точці поля, який напрямлений за нормаллю до |
||||||||||||||||||
поверхні рівня (в бік зростання A(r )) та довжина якого дорівнює ¶f |
¶n , |
|||||||||||||||||
де n – орт нормалі до поверхні рівня |
|
в даній |
точці простору |
(в |
бік |
|||||||||||||
зростання A(r )). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У випадку прямокутної декартової системи координат |
|
|
||||||||||||||||
|
|
|
|
|
¶A |
|
|
¶A |
¶A |
= |
|
|
|
|
||||
grad A = A = i |
¶x |
+ j |
¶y |
+ k |
¶z |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
¶A |
|
¶A |
|
¶A |
|
|
¶A |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||||||
= i |
|
+ i |
|
+ i |
|
|
|
= i |
|
, |
|
a =1,3. |
(3.24) |
|||||
|
¶x |
|
|
|
¶x |
|
||||||||||||
1 ¶x |
2 |
|
3 ¶x |
|
a |
|
|
|
|
|
|
|
||||||
1 |
|
2 |
|
|
|
3 |
|
|
|
a |
|
|
|
|
|
|
|
|
76

Проекціями вектора grad A на координатні осі є ¶A ¶x, ¶A
¶x, ¶A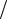 ¶y, ¶A
¶y, ¶A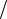 ¶z . Таким чином скалярне поле A = A(r ) утворює векторне поле градієнта grad A .
¶z . Таким чином скалярне поле A = A(r ) утворює векторне поле градієнта grad A .
Операція “дивергенція” визначається як скалярний оператор над векторним полем a , оскільки результатом його дії на векторне поле є скаляр. Векторне поле відрізняється від скалярного тим, що в кожній точці простору крім абсолютного значення задано також його напрямок
(наприклад, поле швидкості, імпульсу тощо). За фізичним змістом дивергенція - це диференціальна характеристика векторного поля або деякої субстанції, яка відповідає за процеси проникнення даної субстанції скрізь границі об’єму, в якому вона розглядається. Дивергенція швидкості, наприклад, чисельно дорівнює швидкості відносного змінення питомого об’єму з часом і відповідає за розтягнення або стиснення об’єму без його деформації. Дивергенція питомого імпульсу дорівнює швидкості змінення густини (рівняння неперервності), тобто відповідає за наявність джерел та стоків даної субстанції.
Дивергенція векторного поля a |
математично представляє |
собою |
||||||||||||||||
скалярний добуток оператора “набла” на векторну функцію a |
= (ax , ay , az ) |
|||||||||||||||||
|
( |
|
) |
|
|
¶a |
x + |
¶ay |
|
¶a |
z = |
|
|
|||||
div a = a |
|
= |
|
|
¶y |
+ |
|
|
|
|||||||||
|
|
|
|
|
|
¶x |
|
|
¶z |
|
|
|||||||
= ¶a1 |
+ |
¶a2 + |
¶a3 |
|
= |
¶aa |
, |
a = |
|
. |
|
(3.25) |
||||||
|
1,3 |
|
||||||||||||||||
¶x |
|
|
||||||||||||||||
¶x |
|
¶x |
|
|
|
¶x |
|
|
|
|
|
|
|
|||||
1 |
|
2 |
|
|
|
3 |
|
|
|
a |
|
|
|
|
|
|
|
|
Таким чином векторне поле a = (ax , ay , az ) перетворюється на скалярну
характеристику дивергенція div a .
Операція “ротор” визначається як векторний оператор над векторним полем a , оскільки результатом його дії на векторне поле є вектор. Ротор вектора швидкості називається вихором швидкості. За фізичним змістом він представляє собою подвійну кутову швидкість обертання. Його математичний вираз через оператор Гамільтона представляє собою
векторний добуток оператора “набла” на векторну функцію a = (ax , ay , az )
rot a |
=[ ´a]= |
|
i |
j |
k |
|
i1 |
i2 |
i3 |
|
|
|
|
|
|||||||||
|
¶ ¶x ¶ ¶y |
¶ ¶z |
= |
¶ ¶x1 |
¶ ¶x2 |
¶ ¶x3 |
|
= |
|||
|
|
|
ax |
ay |
az |
|
a1 |
a2 |
a3 |
|
|
77
|
æ |
¶a |
- |
¶a |
ö |
|
æ |
¶a |
- |
¶a |
= i |
ç |
3 |
2 |
÷ |
+ i |
ç |
1 |
3 |
||
1 |
ç |
|
÷ |
2 |
ç |
|
||||
¶x |
|
¶x |
÷ |
¶x |
|
¶x |
||||
|
ç |
|
|
ç |
|
|||||
|
è |
2 |
|
3 |
ø |
|
è |
3 |
|
1 |
ö
÷
÷+
÷
ø
|
æ¶a |
|
¶a |
ö |
|
|
|
ç |
2 |
|
1 |
÷ |
|
i |
|
- |
|
÷. |
(3.26) |
|
|
|
|||||
3 |
ç |
¶x |
|
¶x |
÷ |
|
|
ç |
|
|
|||
|
è |
1 |
|
2 |
ø |
|
Проекціями вектора |
rot a на координатні осі є (¶a3 |
¶x2 -¶a2 ¶x3 ), |
(¶a1 ¶x3 -¶a3 ¶x1), |
(¶a2 ¶x1 -¶a1 ¶x2 ). Таким чином |
векторне поле |
a = (ax , ay , az ) утворює нове векторне поле ротора rot a . |
|
|
Оператор Гамільтона використовується в багатьох прикладних задачах геофізичної гідродинаміки. У випадку складного добутку двох або більше множників з участю оператора “набла”, операції слід виконувати послідовно, приоритетною вважаючи операцію в дужках.
3.3.1 Рекомендації по вивченню теми
Тема «Оператор Гамільтона» знайомить студентів з використанням символічного вектору, так званого оператору Гамільтона, до отримання диференціальних характеристик векторних та скалярних полів геофізичних величин, також розглядаються суми за Ейнштейном. Застосування оператору Гамільтона виявляється дуже зручним у багатьох питаннях векторного аналізу, який є досить поширеним в геофізичній гідродинаміці. Застосування сум за Ейнштейном є доцільним для скороченого запису членів рівнянь, які мають однакову структуру, внаслідок чого самі рівняння геофізичної гідродинаміки набувають більш компактної форми.
Таким чином, студент по вивченні теми повинен знати: визначення оператору Гамільтона, його властивості і математичний запис, а також вміти застосувати його для визначення диференціальних характеристик полів геофізичних величин, і вміти отримувати компактну форму запису рівнянь та членів рівнянь з використанням сум за Ейнштейном.
Ознайомитись з цією темою можна також в літературі: [2] - стор. 148-163.
3.3.2 Приклади розв’язання типових задач
Задача № 1. |
|
¶ua |
|
Умова. Запишіть вираз |
u |
для i = 2 в повному вигляді |
|
|
i ¶x |
|
|
|
|
a |
|
(у вигляді суми).
78
Розв’язання задачі.
Присутність в математичному виразі індексу a , що повторюється, вказує на наявність за ним “суми за Ейнштейном”. За індексом i суми немає, оскільки він не повторюється. Він приймає стале значення i = 2 .
u |
¶ua |
= u |
|
¶ua |
. |
|
|
||||
i ¶x |
2 ¶x |
||||
|
a |
|
a |
||
Оскільки в умові задачі не вказується, які значення приймає індекс a , вважаємо, що він змінюється від 1 до 3 або приймає значення x, y, z . Отже
остаточно отримуємо
u |
¶ua = u |
|
|
¶ua |
= u |
|
|
¶u1 |
|
+ u |
|
¶u2 |
+ u |
|
¶u3 . |
||||||
|
|
|
|
|
|
|
|||||||||||||||
i ¶x |
|
2 |
|
¶x |
|
|
|
2 ¶x |
|
|
|
|
2 ¶x |
|
|
2 ¶x |
|||||
|
a |
|
|
|
a |
|
|
|
1 |
|
|
|
|
2 |
|
|
|
3 |
|||
або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶uy |
|
|
|
|
|
|
|
|
¶u |
|
|
|
|
¶u |
x |
|
|
|
|
|
|
|
¶u |
z |
|
|||
|
u |
a |
= u |
|
|
+ u |
|
|
|
|
|
+ u |
|
|
|
||||||
|
|
|
|
|
|
¶y |
|
|
|
||||||||||||
|
i ¶x |
|
|
|
y |
¶x |
|
|
|
y |
|
|
y |
¶z |
|
||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
для i = 2 (для прямокутної декартової |
системи |
координат це означає, |
|||||||||||||||||||
що i = y ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача № 2. |
|
|
|
Умова. Запишіть в декартовій системі координат та в термінах “суми |
|||
за Ейнштейном” вираз |
|
якщо вектор V має складові Vx , |
Vy , Vz , а |
2 ( V ) , |
|||
|
, y , z . |
|
|
вектор – складові x |
|
|
|
Розв’язання задачі. |
|
|
|
Маємо випадок складного |
добутку трьох множників з |
участю |
|
оператора “набла”. Операції слід виконувати послідовно, приоритетною є операція в дужках, отже її виконуємо першою. Вона представляє собою скалярний добуток оператора “набла” на вектор швидкості або
дивергенцію вектора швидкості div V . Можна скористатись відомим
виразом для div V , або означенням, згідно якому скалярний добуток – сума
добутків відповідних проекцій векторів на координатні осі. В будь–якому випадку для прямокутної декартової системи координат:
79
|
|
|
¶V |
¶Vy |
|
¶V |
|
|
( V ) = div V |
= |
|
x + |
|
+ |
|
z . |
|
|
¶y |
|
||||||
|
|
|
¶x |
|
¶z |
|||
Наступною є операція множення вектора |
на отриманий скаляр. |
|||||||
Оскільки вектор має складові |
|
x , |
y , |
z , то |
в декартовій системі він |
|||
має вигляд |
|
|
|
|
|
|
|
|
w = i wx + jwy + k wz .
Отже остаточно в декартовій системі координат |
|
вираз |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
2 ( V ) |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
представляє собою вектор і має вигляд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
æ |
¶V |
x |
|
|
|
¶Vy |
|
|
¶V |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ¶V |
|
|
|
|
¶Vy ¶V |
ö |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
ç |
|
|
|
|
|
|
|
|
|
|
|
z ÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z ÷ |
|
|
|
|
|||||||
2w( V ) = 2w |
ç |
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
÷ |
= 2(i wx |
+ jwy |
+ k wz )ç |
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
÷ |
= |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
ç |
¶x |
|
|
|
¶y |
|
|
|
|
|
¶z |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
¶x |
|
|
|
|
¶y |
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
||||||||||
|
|
|
|
è |
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
¶z ø |
|
|
|
|
||||||||||||||||
|
æ |
¶V |
|
|
¶Vy |
|
|
¶V |
ö |
|
|
|
|
|
æ¶V |
|
|
¶Vy |
|
|
¶V |
|
ö |
|
|
|
æ |
¶V |
|
|
|
|
¶Vy |
|
|
|
¶V |
ö |
||||||||||||||||||||||||
|
ç |
x |
|
|
|
|
|
|
|
|
|
|
z |
÷ |
|
|
|
|
|
|
ç |
|
|
x |
|
|
|
|
|
|
|
|
z |
÷ |
|
|
|
|
|
|
ç |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
z ÷ |
|||||
= i |
2wx ç |
|
+ |
|
|
|
|
|
+ |
|
|
|
÷ |
+ j 2wy |
ç |
|
|
|
+ |
|
|
|
|
+ |
|
|
÷+ k |
2wz ç |
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
÷. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
ç |
¶x |
|
|
|
¶y |
|
|
|
|
|
¶z |
÷ |
|
|
|
|
|
|
ç |
|
¶x |
|
|
|
¶y |
|
|
¶z |
÷ |
|
|
|
|
|
|
ç |
|
¶x |
|
|
|
|
|
¶y |
|
|
|
|
÷ |
||||||||||||
|
è |
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
è |
|
|
|
|
|
|
ø |
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
¶z ø |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В термінах “суми за Ейнштейном” вираз 2 ( V ) можна представити так: |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
¶V |
|
¶V |
|
|
¶V |
ö |
|
¶a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
1 |
+ |
|
|
2 |
+ |
|
|
3 |
÷ |
2w |
|
|
|
a |
, |
|
|
a =1,3. |
|
|
|
|
|
|
|
|||||||||||||||
|
2w( V ) = 2w div V = 2wç |
¶x |
¶x |
¶x |
÷ = |
¶x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
1 |
|
|
|
2 |
|
|
|
|
3 |
ø |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Оскільки вектор в термінах “суми за Ейнштейном” можна представити |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
як |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w = i1w1 + i2w2 + i3w3 = ibwb , |
|
|
|
|
b = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1,3, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
то остаточно вираз |
|
|
|
|
|
|
|
|
|
в термінах “суми за Ейнштейном” набуває |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
2 ( V ) |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вигляду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶a |
|
|
|
|
|
|
¶a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2w( V ) = |
2w |
div V |
= |
2w |
|
a |
= 2i |
w |
|
|
|
a |
, |
|
|
|
a =1,3, |
|
|
b =1,3. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶x |
|
|
|
b |
b |
|
¶x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
80
3.3.3 Контрольні запитання до теми
1.Оператор Гамільтона. Визначення та фізичне застосування.
2.Поняття “суми за Ейнштейном”.
3.Оператор “набла” в термінах “суми за Ейнштейном”.
4.Основні диференціальні характеристики векторних та скалярних полів.
5.Визначення скалярного поля та поверхні рівня.
6.Градієнт скалярного поля. Визначення, фізичний сенс.
7.Градієнт скалярного поля. Його проекції на координатні осі у випадку прямокутної декартової системи координат та запис у термінах “суми за Ейнштейном”.
8.Дивергенція векторного поля. Визначення, фізичний сенс.
9.Дивергенція векторного поля. Її запис у термінах “суми за Ейнштейном”.
10.Ротор векторного поля. Визначення, фізичний сенс.
11.Ротор векторного поля. Його проекції на координатні осі у випадку
прямокутної декартової системи координат.
12.Градієнт скалярного поля є векторним чи скалярним полем?
13.Дивергенція векторного поля є векторним чи скалярним полем? 14.Ротор векторного поля є векторним чи скалярним полем?
15.В якій послідовності слід розв’язувати задачі складного добутку
двох або більше множників з участю оператора “набла”?
3.3.4 Задачі для самостійного розв’язання
1.Запишіть вираз grad f з використанням оператора “набла”.
2.Запишіть вираз divV з використанням оператора “набла”.
3.Запишіть вираз rotV з використанням оператора “набла”.
4. Запишіть вираз |
i |
для i = 2 в повному вигляді (у вигляді |
|
x |
|||
|
|
||
суми). |
|
|
|
|
|
5.Запишіть вираз в повному вигляді (у вигляді суми).
6.Запишіть в декартовійx системі координат вираз (2 )V , якщо вектор має складові x , y , z .
7.Запишіть в декартовій системі координат вираз 2 ( V ) , якщо
має складові u , , w.
8.Запишіть в декартовій системі координат вираз ( V )T , якщо
має складові Vx , Vy , Vz .
81
9. |
Запишіть вираз |
|
T |
в повному вигляді (у вигляді суми). |
|
|
|||
|
x |
|
||
|
|
|
|
|
10. |
Запишіть вираз |
(V )V в декартовій системі координат, якщо |
||
вектор V має проекції на координатні осі Vx , Vy , Vz .
3.4 Число Россбі–Кібеля і прискорення Коріоліса
Угеофізичній гідродинаміці, в основному, вивчаються великомасштабні процеси. Чи буде явище великомасштабним залежить від його характерного просторового масштабу та його динаміки, тобто характерної швидкості.
Угеофізичній гідродинаміці великомасштабними вважаються такі рухи, на які істотно впливає обертання Землі. Під характерним просторовим масштабом руху L будемо розуміти деяку довжину фізичної системи, що найбільш часто зустрічається. Отак, за характерну довжину у
горизонтальній площині можна прийняти відстань, на якій істотно
змінюються характеристики циркуляції, наприклад, середня швидкість потоку змінює свій напрямок на протилежний. Аналогічно через U
позначимо характерний масштаб горизонтальної швидкості руху, тобто
швидкість, що є типовою для даної фізичної системи (середня швидкість
руху).
Наприклад, для великомасштабних атмосферних процесів масштаб L має порядок 1000 км, а масштаб U – 20 м/с. Час, який потрібен для переміщення на відстань L частинки рідини, яка рухається зі швидкістю
U , дорівнює L U . Якщо цей проміжок істотно менше періоду обертання
U . Якщо цей проміжок істотно менше періоду обертання
Землі, то кількісні характеристики руху будуть мало відрізнятися в інерціальній і неінерціальній системах відліку протягом часу L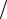 U .
U .
Періодом обертання називається час, протягом якого тіло повертається навколо нерухомої осі обертання на кут, що дорівнює 2 . Таким чином, можна припустити, що вплив обертання стає істотним за умови
|
|
|
L |
|
1 |
, |
|
|
(3.27) |
|
|
U |
|
|
|||||
|
|
|
|
|
|
|
|||
що еквівалентно |
|
|
|
|
|
|
|
|
|
|
U |
1 |
або |
|
U |
1, |
(3.28) |
||
|
L |
|
2 L |
||||||
|
|
|
|
|
|
|
|
||
(сенс уведення у знаменник (3.28) множника «2» стане зрозумілим із подальшого викладу).
82
