Geofizichna_gidrodinamika_statsionar

Можна розв’язати й зворотну задачу. Використовуючи рівняння (2.21), за заданою функцією течії можна визначити поле швидкості

Vx =	¶Y ,	Vy	= -	¶Y .	(2.23)
	¶y			¶x
Потенційним називається безвихровий рух. Умова існування
потенційного руху:
	rotV = 0.				(2.24)

Вивчення цього руху зводиться до визначення потенціала швидкості j , що пов'язаний з вектором швидкості

V = gradj,

(2.25)

або в проекціях на координатні осі

Vx =	¶j	,	Vy =	¶j	,	Vz =	¶j .	(2.26)
	¶x			¶y			¶z

За заданим полем швидкостей можна знайти потенціал швидкості, використовуючи вираз для повного диференціалу:

æ	¶j		¶j	¶j	ö	( x			)
ç					÷		y	z
		dx +		dy +						(2.27)
j = ò ç					dz÷= ò V		dx +V	dy +V	dz .
ç	¶x		¶y	¶z	÷
è					ø

Отриманий потенціал буде визначено з точністю до адитивної константи інтегрування C .

Використовуючи рівняння (2.26), можна розв’язати й зворотну задачу, тобто за заданим потенціалом визначити поле швидкості, представлене компонентами (2.25).

Відоме рівняння Коші-Римана, що виражає зв'язок потенціала та функції течії:

¶j	=	¶Y	,	¶j	= -	¶Y .	(2.28)
¶x		¶y		¶y		¶x

43

Під час вивчення плоских потенціальних та соленоідальних рухів нестисливої рідини вводиться поняття еквіпотенціальних ліній та ліній течії, відповідні рівняння яких можна записати у вигляді:

j(x, y) = Const,

Y(x, y) = Const.

(2.29)

З умови Коші-Римана випливає:

¶j		¶Y	+	¶j		¶Y	= 0,	(2.30)
¶x		¶x		¶y		¶y
тобто кожна крива сімейства			j(x, y)= Const					перетинається під прямим

кутом з будь-якою кривою сімейства ліній Y(x, y) = Const . Отже потенціальні лінії та лінії течії взаємно перпендикулярні.

2.4.1 Рекомендації по вивченню теми

Під час вивчення теми студент повинен опанувати такі поняття, як потенціал швидкості та функція течії, потенціальні лінії та лінії течії; навчитись розраховувати складові швидкості за відомими потенціалом швидкості або функцією течії та розв’язувати обернені задачі.

Особливу увагу слід приділити зв’язку між потенціалом швидкості та функцією течії (рівняння Коші–Рімана) та зв’язку між потенціальними лініями та лініями течії.

Рекомендована література по вивченню теми: [3] – том I, стор. 31–44, [4] – стор. 69–84, [11] – стор. 43–48

2.4.2 Приклади розв’язання типових задач

Задача № 1.

Умова. Знайти вираз для дивергенції швидкості та скласти рівняння неперервності для рідкого струму, якщо рух стаціонарний, а проекції швидкостей на координатні осі в залежності від положень точок струму в просторі визначаються рівняннями:

Vx = 2x2 + y,

Vy = 2 y2 + z,

Vz = 2z2 + x.

44

Розв’язання задачі.

Дивергенція швидкості за означенням

divV = ¶¶Vxx + ¶¶Vyy + ¶¶Vzz .

В результаті диференціювання отримуємо: divV = 4(x + y + z).

Рівняння неперервності:

¶¶rt + divrV = 0,

або

¶r

+V

¶r

+V

¶r

+V

¶r

çæ

¶Vx

¶Vy

x

y

z

+ rç

+

¶t

¶x

¶y

¶z

ç

¶x

¶y

è

¶Vz ö÷

+ ÷ = 0.

÷

¶z ÷ø

Оскільки рух вважається стаціонарним,

¶¶rt = 0,

отже рівняння неперервності має вигляд:

¶¶rx (2x2 + y)+ ¶¶ry (2 y2 + z)+ ¶¶rz (2z2 + x)+ 4r(x + y + z)= 0.

Для випадку нестисливої рідини

r(x, y, z) = Const

і рівняння неперервності значно спрощується:

¶¶rt + rdivV = 0 .

45

Якщо рух до того ж стаціонарний, воно в результаті диференціювання набуває вигляду:

x + y + z = 0.

Задача № 2.

Умова. Знайти вираз для функції течії, якщо поле швидкостей потоку задовольняє рівнянню:

j = 2xy.

Розв’язання задачі.

Повний диференціал функції течії визначається через компоненти поля швидкості:

dY =Vxdy -Vydx.

Відповідні компоненти можна відновити за заданим потенціалом:

	Vx =		¶j	,	Vy =	¶j .
			¶x			¶y
Згідно з умовою задачі,
Vx =	¶j	= 2 y,			Vy =	¶j	= 2x ,
	¶x					¶y

отже повний диференціал функції течії

dY = 2 ydy - 2xdx.

Інтегруючи, отримуємо функцію течії у вигляді:

Y = 2(y2 - x2)+ C,

де C - константа інтегрування.

46

Задача № 3.

Умова. Знайти складові вектора кутової швидкості та вектора вихору швидкості, якщо проекції вектора швидкості на координатні осі визначаються співвідношеннями:

Vx = y + 2z,

Vy = z + 2x,

Vz = x + 2 y.

Розв’язання задачі.

Компоненти вектора кутової швидкості за означенням:

			1	æ	¶V					ö
				ç		z		¶Vy ÷
wx =							-			÷
				ç						÷,
			2	ç	¶y			¶z		÷
				è						ø
			1	æ¶V		x		¶V		ö
w		=		ç			-		z ÷
	y									÷,
			2	ç						÷
				è ¶z				¶x ø
			1	æ	¶Vy					ö
				ç				¶Vx ÷
wz =							-			÷
				ç						÷.
			2	ç	¶x					÷
				è				¶y ø

Отже в результаті інтегрування отримуємо:

w	x	= 1	(	2	-1	= 1 ,	w	y	= 1	,	w	z	= 1 .
		2			)	2			2				2

Складові вектора вихору швидкості визначаються через складові вектора кутової швидкості за правилом:

Wx=2wx , Wy = 2wy , Wz = 2wz.

Отже

Wx=1, Wy =1, Wz =1.

2.4.3Контрольні запитання до теми

1.Дайте визначення плоского руху.

2.Яка фізична величина є основною характеристикою обертального руху?

3.Як пов’язані вектор вихору швидкості та вектор кутової швидкості обертання рідкої частинки?

4.Дайте визначення завихреності.

5.Дайте визначення соленоідального руху.

47

6.Запишіть умову соленоідальності руху.

7.Який фізичний зміст умови соленоідальності руху?

8.Який сенс введення функції течії для соленоідального руху?

9.Як пов'язана функція течії з вектором швидкості рідкої частинки?

10.З якою точністю визначається функція течії?

11.Дайте визначення потенційного руху.

12.Запишіть умову існування потенційного руху.

13.Яка характеристика вводиться для опису потенційного руху?

14.Як пов'язаний потенціал швидкості з вектором швидкості рідкої частинки?

15.З якою точністю визначається функція течії?

16.Як пов’язані потенціал та функція течії?

17.Дайте визначення еквіпотенціальних ліній та ліній течії.

18.Як взаємно розташовані потенціальні лінії та лінії течії?

2.4.4Задачі для самостійного розв’язання

1. Знайти вираз для дивергенції швидкості, якщо проекції вектора швидкості на координатні осі визначаються співвідношеннями: Vx = ay2 + 2z, Vy = bz + 2x, Vz = x + 2 y2 , де a і b – відмінні від нуля

довільні сталі.

2. Знайти складові вектора вихору швидкості, якщо проекції вектора швидкості на координатні осі визначаються соотношениями:

співвідношеннями: Vx = ay2 + 2z, Vy = z2 + 2bx, Vz = ax3 + 2 y2 , де a і

b– відмінні від нуля довільні сталі.

3.Знайти компоненти вектора кутової швидкості обертання, якщо компоненти лінійної швидкості рідкої частинки змінюються в залежності

від координат за співвідношеннями: Vx = ay2z, Vy = 2bzy, Vz = 2ay2 , де

aі b – відмінні від нуля довільні сталі.

4.Знайти складові вектора швидкості соленоідального руху, якщо

функція течії Y = 2x2 y..

5. Знайти складові вектора швидкості потенціального руху, якщо потенціал швидкості j = 2xy2.

6. Знайти вираз для завихреності, якщо складові вектора швидкості вздовж осей x та y задані співвідношеннями: Vx = ayz, Vy = -2bzy , де a

іb – відмінні від нуля довільні сталі.

7.Знайти вираз для плоскої дивергенції, якщо проекції вектора швидкості на координатні осі визначаються співвідношеннями:

48

Vx = ay2z + bx3, Vy = 2bzy + x3, де a і b – відмінні від нуля довільні

сталі.

8. Довести, що плоский рух є безвихровим, якщо проекції вектора швидкості на вісі x та y задані співвідношеннями:

Vx = ax3 + b, Vy = -2 y + ay2 , де a і b – відмінні від нуля довільні сталі.

9. Довести, що плоский рух є соленоідальним, якщо проекції вектора швидкості на вісі x та y задані співвідношеннями:

Vx = -2 y + ay2, Vy = ax3 + b , де a і b – відмінні від нуля довільні сталі.

10. Знайти дивергенцію радіуса-вектора r , проекції якого на координатні осі дорівнюють x, y, z .

2.5 Циркуляція вектора швидкості

Щоб ввести поняття циркуляції швидкості, розглянемо довільну замкнену геометричну криву, що складається з фізичних частинок, що знаходяться у рідині, яка рухається. За позитивний напрямок будемо вважати напрямок обходу проти годинникової стрілки. Виділимо на

замкненій кривій спрямовані елементарні відрізки dl		і	відзначимо	на
кожному з них складову швидкості вздовж кривої Vl		V	cos , де V	-

вектор швидкості, – кут між вектором швидкості і напрямком дотичної. Назвемо потік вектора швидкості вздовж замкненої кривої циркуляцією швидкості або просто циркуляцією. Тоді під циркуляцією швидкості за замкненим контуром будемо розуміти криволінійний інтеграл

від скалярного добутку (Vdl ) за цим контуром:

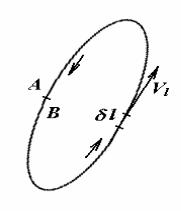
Рисунок 2.9 – Визначення потоку і циркуляції швидкості

49

C (Vdl ) V dl cos(Vdl ) Vl dl ,			(2.31)
l	l	l

або

C Vl dl	V	l l ,	(2.32)
l

де V l - середнє значення складової швидкості вздовж всієї довжини контуру l . З приведених визначень очевидно, що якщо замкнена крива розділена на відрізки, то циркуляція є сумою потоків вздовж складових

відрізків. Представимо далі скалярний добуток (Vdl )		у координатній
формі:
C (Vdl ) udx vdy wdz ,		(2.33)
l	l

де u, v, w – проекції вектора швидкості, а dx, dy, dz - проекції елемента

контура dl на осі декартової системи координат.

Як видно з виписаних формул, циркуляція швидкості являє собою скалярну величину, що характеризує кількісно міру руху частинок за замкненим контуром l . Нагадаємо, що в правій системі координат обхід

виконується проти годинникової стрілки, тому С>0. Це означає, що сумарна обертальна складова швидкості спрямована проти годинникової стрілки. Тоді при С<0 сумарна складова обертального руху буде за годинниковою стрілкою. Очевидно, що в циклоні С > 0, а в антициклоні C<0. Якщо циркуляція швидкості C 0, то таке поле називається потенційним. Підінтегральний вираз буде дорівнювати повному диференціалу від потенціала швидкості :

d udx vdy wdz ,

а складові відповідно: u d	,	v d	,	w d .
dx		dy		dz

Теорема Стокса стверджує, що циркуляція вздовж замкненої кривої дорівнює площині, яку охоплює ця крива, помноженій на нормальну до цієї площини складову вихору. Це твердження відоме може бути доведене для будь-якої кривої: плоскої чи просторової. Проте це найпростіше показати на прикладі контуру у вигляді прямокутника (рис. 2.10).

50

Рисунок 2.10 – Циркуляція швидкості вздовж границь елементарної площини

Розглянемо розрахунок циркуляції по крокам. Напрямок обходу цього контура виберемо позитивним, тобто проти годинникової стрілки, а у вузлах отримаємо наступні значення складових швидкостей:

1 – u , v ;

2– u ux x, v vx x ;

3– u ux x uy y, v vx x vy y ;

4– u uy y,v vy y .

Обчислимо циркуляцію швидкості для цього елементарного контуру. При цьому складові швидкості на кожному відрізку будуть враховуватися тільки уздовж лінії обходу (нормальні складові не розглядаються) і вважатися середніми на даному відрізку як півсума на його кінцях. Тоді

C 12 (u u ux x) x 12 (v vx x v vx x vy y) y

51

1 (u

u

x

u

y u u

y) ( x) 1 (v

v

y v) ( y)

x

y

y

2

y

2

(

v

u

) x y.

x

y

Позначивши

через А x y

–

площину

прямокутника, а

z

v

u -

вихор

у

площині ХОУ

як

нормальну

складову вихору,

x

y

маємо остаточно

C A z

чи z

C

.

(2.34)

A

Звідси може бути дана інтерпретація, що вихор - це циркуляція уздовж одиничної площини.

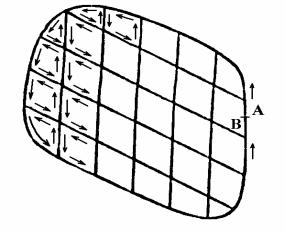
Якщо тепер розглянути цей результат для кінцевої площини А (рис. 2.10), то сума вихорів усередині довільної замкненої кривої буде дорівнювати сумі циркуляцій вздовж елементарних, одиничних площадок, але, оскільки потоки уздовж загальних границь анулюються, взаємно знищуються, то решта сум потоків уздовж зовнішніх границь дорівнює циркуляції уздовж замкненої кривої, що охоплює дану площину А. Тоді маємо

C z A.	(2.35)
А

Рис. 2.11 – Циркуляція за замкненим контуром

52