Geofizichna_gidrodinamika_statsionar

на поверхні, що її обмежує; сумарна поверхнева сила, яка прикладена до частинки рідини, пропорційна площі поверхні, що її обмежує.

Найважливішою масовою силою є сила притягання. Найважливішими поверхневими силами є сила баричного градієнту і сила в’язкості.

3.1.3Рекомендації по вивченню теми

Вцій темі розглядається динаміка ідеальної рідини в інерціальній (необертовій) системі відліку та математичний апарат, що використовується для її опису. Знайомство з динамікою атмосфери та океанічних процесів доцільно починати з найпростіших моделей цих процесів, однією з таких моделей і є модель динаміки ідеальної рідини в інерціальній системі відліку.

Під час вивчення даної теми студент має звернути увагу на такі базові знання та вміння, як поняття інерціальної та неінерціальної систем відліку; поняття масових та поверхневих сил; сил, що діють в інерціальній системі відліку; зв’язок між законом збереження імпульсу, другим законом Ньютона та рівнянням руху.

Література, яка рекомендується для більш глибокого вивчення теми, є

наступною: [3] – том I, стор. 44–54, [4] – стор. 98–109, [11] – стор. 12–22, 59–71.

3.1.4Контрольні питання до теми

1.Дайте визначення інерціальної системи відліку.

2.Дайте визначення неінерціальної системи відліку.

3.До якої системи відліку відноситься Земля? Чому?

4.Як відрізняються між собою масові та поверхневі сили?

5.Які сили відносять до масових (поверхневих) сил?

6.Які сили діють в інерціальній системі координат?

3.2Рівняння руху у неінерціальній (обертовій) системі відліку для в’язкої рідини

Як вже було сказано вище, другий закон Ньютона не виконується для неінерціальних систем відліку. Для того щоб другий закон Ньютона був справедливим для частинки, що розглядається в неінерціальній системі відліку, необхідно отримати новий вираз для прискорення, який містив би у собі прискорення, обумовлене силами, що діють на дану частинку з боку інших тіл (рівняння 3.13), та доданки, які описують прискорення неінерціальної системи відносно інерціальної системи відліку.

63

3.2.1Різниця між прискореннями в необертовій та обертовій системах відліку

За теоремою Коріоліса різниця між прискореннями в необертовій та обертовій системах відліку задається наступним виразом:

dV

dV

d

(3.14)

I

R

2

VR

r

dt

r ,

dt

I

dt

R

де

– кутова швидкість обертання Землі;

VR – швидкість тіла відносно обертової системи відліку;

VI

– швидкість тіла відносно необертової системи відліку;

r

– радіус–вектор точки.

Фізичний сенс членів, що стоять у правій частині рівняння (3.14):

– прискорення Коріоліса;

2

V

R

r – доцентрове прискорення;

d

dt

r

–

прискорення,

що

зумовлено

зміною

самої

швидкості

обертання Землі.

З великим ступенем точності можна вважати, що швидкість обертання Землі з часом не змінюється, і, тому, нехтуючи третім складником у формулі (3.14), її можна переписати у вигляді:

dV

dV

I

R

2

VR

r ,

(3.15)

dt

dt

I

R

Отримаємо вираз для рівнянь руху у системі координат, що

обертається. З цією метою підставимо вираз (3.15) у рівняння (3.13):

1

dV

R

2 VR

r

p s ,

(3.16)

dt

R

тобто при переході до обертової системи відліку права частина формули (3.12) залишається без змін, а у лівій частині з’являються два додаткові члени. Оскільки надалі рух рідини розглядається лише в обертовій системі відліку, то у подальшому викладенні опустимо індекс „R”.

Якщо тепер прискоренні Коріоліса і доцентрове прискорення перенести у праву частину рівняння (3.14), то їх можна тлумачити як сили,

64

які здаватимуться спостерігачу в обертовій системі відліку деякими додатковими силами інерції – силою Коріоліса ( 2 V ) і відцентровою

силою (C ( r )) , що віднесені до одиниці маси і відрізняються від відповідних прискорень тільки знаком.

3.2.2Сила тяжіння

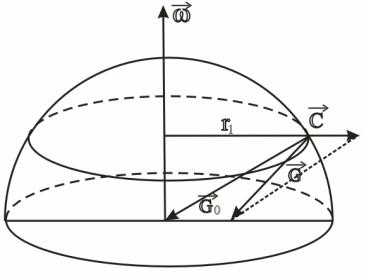
І тіла, що покояться, і тіла, що рухаються відносно земної поверхні зазнають впливу відцентрової сили, яка спрямована уздовж радіусу ( r1 )

кола обертання точки від центру (рис. 3.2); також всі тіла, розташовані поблизу Землі знаходяться під впливом сили притягання. У зв’язку з цим, силу притягання і відцентрову силу об’єднують в одну, і називають силою тяжіння (рис. 3.2) матеріальної точки.

Рисунок 3.2. – Сила тяжіння G як векторна сума сил земного

притягання G0 і відцентрової сили C .

На рисунку неможливо витримати вірне співвідношення величин G0

та C , оскільки відцентрова сила занадто мала в порівнянні з силою земного притягання. Сила тяжіння максимальна на полюсах і мінімальна на екваторі.

Для відцентрової сили, якщо розкрити подвійний векторний добуток, отримаємо вираз: C 2r1, де r1 – радіус кола обертання точки.

65

До відцентрової сили можна застосувати потенціальну функцію c так, що

		C c ; c	2r12						2
							r			.	(3.17)
						2
			2
G	Таким	чином, силу тяжіння, G ,					можна				представити як
	G0 C	s c .

Потенціальний характер сили притягання, G0 , і відцентрової сили, C ,

дозволяє і для поля сили тяжіння, G , ввести скалярну характеристику – потенціал s c , пов’язаний з G співвідношенням: G g , де g – прискорення вільного падіння, або прискорення сили тяжіння.

3.2.3Сила Коріоліса

На тіло, що покоїться в обертовій системі координат з сил інерції діє лише відцентрова сила. Якщо ж тіло рухається відносно обертової системи

координат, то на тіло окрім відцентрової сили, діятиме ще сила Коріоліса: 2 V .

Вона обертається на нуль в двох випадках: по–перше, якщо тіло покоїться відносно земної поверхні ( V 0 ); по–друге, якщо рух тіла

спрямований паралельно осі обертання.

Сила Коріоліса завжди перпендикулярна до швидкості і, отже, не виконує роботу. Спостерігачу, який обертається з кутової швидкістю , здається, що сила Коріоліса намагається відхилити рідку частинку вправо (у північній півкулі) та вліво (у південній півкулі).

Для розуміння дії сили Коріоліса розглянемо наступний приклад: рух деякого об’єкту, запущеного без тертя з північного полюсу уздовж Гринвіцького меридіану. На рис. 3.3 показано частину траєкторії цього об’єкту у тривимірному просторі (точкова лінія показує рух об’єкті, як його бачить спостерігач, що знаходиться на Землі, а пунктирна лінія показує рух об’єкту, як його бачить спостерігач в інерціальній системі відліку). Для спостерігача в інерціальній системі відліку рух тіла буде впродовж всього часу відбуватись уздовж уявної лінії, яка вказуватиме місцеположення Гринвіцького меридіану в момент запуску тіла. Проте для спостерігача, що знаходиться на Землі рух тіла здаватиметься дещо іншим. Нехай за деякий інтервал часу тіло пролітає відстань r , а Земля повертається на кут . Тоді через цей інтервал часу для спостерігача на Землі, тіло опиниться в точці 2, через два інтервали часу – в точці 3. Звідси

66

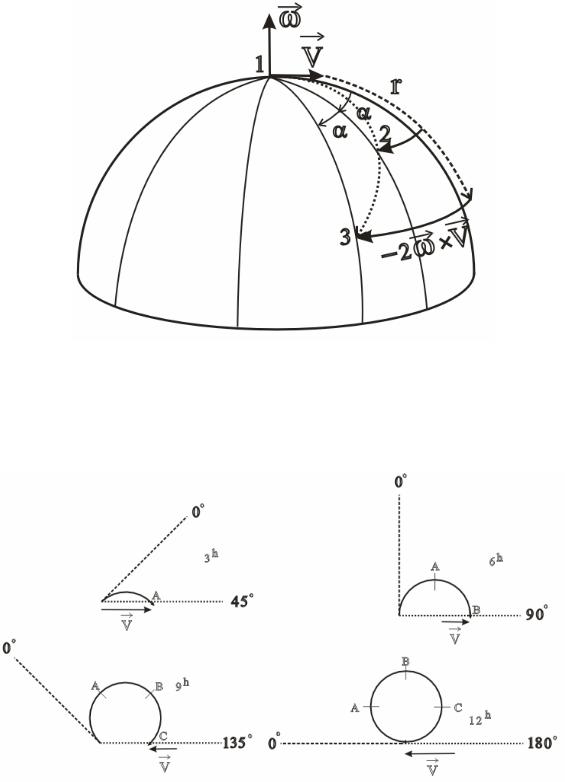
бачимо, що тіло відхилятиметься вправо від вектора швидкості внаслідок дії сили Коріоліса.

Рисунок 3.3 – До впровадження сили Коріоліса

На рис. 3.4 показано траєкторію цього ж об’єкту у горизонтальній площині впродовж 12 годин після запуску.

Рисунок 3.4 – До впровадження сили Коріоліса

67

На рис. 3.4 горизонтальна точкова лінія відзначає позицію, яку мав Гринвіцький меридіан в момент запуску тіла ( t 0 ), а пунктирна лінія – його позицію в 3h, 6h, 9h та 12h після запуску. Горизонтальні стрілки вказують переміщення об’єкту як його бачить спостерігач в інерціальній системі відліку. Суцільні криві показують траєкторію об’єкту, як її бачить спостерігач в неінерціальній системі відліку. Літери A, B і C показують позицію об’єкту відносно обертової системи через тригодинні інтервали.

З урахуванням вищевикладеного рівняння (3.16) приймає вигляд:

		1
dV
dt			p 2 V .	(3.18)

Рівняння (3.18) – це рівняння ідеальної рідини в неінерціальній системі відліку.

3.2.4Сила в’язкості

Для ідеальної рідини єдиною внутрішньою силою є тиск – однозначна скалярна функція p x, y, z,t . Це твердження є справедливим і для в’язкої

рідини, що покоїться.

Проте в’язка рідина, що рухається, відрізняється від ідеальної рідини тим, що в ній розвиваються дотичні напруження, які обумовлені в’язкістю (внутрішнім тертям).

При русі двох сусідніх шарів рідини з різними швидкостями, між цими шарами розвиваються дотичні сили внутрішнього тертя або сили в’язкості. Слід підкреслити, що в’язкість є основна властивість рідких тіл – рідин та газів. Ця властивість викривається тільки при русі і полягає у тому, що рух у в’язкій рідині (газі) передається від шару до шару, причому чиниться опір переміщенню частинок відносно одна одної.

Якщо рідина рухається, то між шарами, що рухаються з різними швидкостями, внаслідок невпорядкованого руху молекул виникає обмін кількістю руху. Молекули безперервно переходять з одного шару в інший, здійснюючи змішування та зчеплення шарів.

Молекули, що переходять із шару, який рухається з великою швидкістю, в шар, який рухається з меншою швидкістю, прискорюють рух цього шару, та навпаки, молекули, що проникають з шару, який рухається повільно, у шар, який рухається швидко, уповільнюватимуть рух останнього (рис. 3.5).

В’язкість грає подвійну роль при русі будь–якої реальної рідини. Спостереження показують, що поле швидкості в реальній рідині є неперервним. Формування такого неперервного поля швидкостей

68

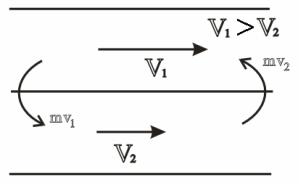
забезпечується впливом в’язкості, яка здійснює безперервну передачу кількості руху від одного шару до іншого. Окрім вирівнювання швидкостей, передача кількості руху від шару до шару супроводжується поглинанням механічної енергії та перетворюванням її в теплову. В цьому випадку ми маємо справу з розсіюванням або дисипацією механічної енергії, обумовленою в’язкістю.

Рисунок 3.5. – До впровадження сили в’язкості (внутрішнього тертя).

З урахуванням сил в’язкості рівняння (3.18) запишемо у вигляді:

dV

1

p 2 VR 1 grad divV V ,

(3.19)

dt

3

де

останні

два

члени

є

математичним

записом

сили

в’язкості,

2

2

2

,

–

кінематичний коефіцієнт в’язкості, а –

x2

y2

z2

коефіцієнт динамічної в’язкості рідини – параметр, що залежить лише від

фізичних властивостей рідини. Якщо рідина є нестисливою ( divV 0 ), то вираз для сили в’язкості спрощується і (3.19) матиме наступний вигляд:

	dV		1
				p 2 V	V .	(3.20)
	dt			R

3.2.5Рекомендації по вивченню теми

В даній темі на відміну від попередньої студент знайомиться з більш складними моделями (тобто рівняннями) динаміки рідини. Рівняння руху, що розглядаються в цьому розділі, більш повно враховують фізику реальних процесів, що відбуваються в океані та атмосфері.

69

По закінченні вивчення теми студент повинен знати:

здійснення переходу від інерціальної до неінерціальної системи відліку;

всі сили, що діють в океані та атмосфері, з яких особливу увагу треба приділити силам інерції;

фізичний механізм формування сили в’язкості, а також роль сили в’язкості при русі рідини.

та вміти:

отримати числові значення для сил, якщо відомо умови при яких відбувається рух рідини;

розрахувати складові сил, користуючись стандартною системою координат;

оцінити вклад різних сил при різних умовах руху рідини. Ознайомитись з цією темою можна також в літературі: [4] – том II,

стор. 369–403, [11] – стор. 72–84.

3.2.6Приклади розв’язання типових задач

Задача № 1.

Умова. Розрахувати лінійну швидкість твердотільного обертання Землі на широті 300. Прийняти радіус Землі рівним 6400 км.

Розв’язання задачі.

З векторної алгебри відома формула, яка пов’язує лінійну швидкість з

кутовою: V r , r – радіус–вектор точки. Розкриваючи цей векторний добуток, отримаємо V r r sin , r .

Рисунок 3.6. – До визначення лінійної швидкості

70

З рис. 3.6

видно, що кут між вектором кутової швидкості та радіусом–

вектором

точки

дорівнює

900 ,

тобто

sin

90

0

cos . Відомо,

що

кутова

V

r

sin , r

r

r

швидкість

дорівнює

7.29 10 5 c 1.

Тоді для

широти

30

0

:

cos

7.29 10

5

c

1

64 10

5

м cos 60

0

233 м/ с.

V

r

Задача № 2.

Умова. Знайти вираз для модуля відцентрової сили.

Розв’язання задачі.

Вираз для відцентрової сили має вигляд C ( r ) . З рис. 3.6 видно, що відцентрова сила може бути виражена через вектор r1 ,

перпендикулярний до осі обертання і спрямований від осі обертання до

частинки.

sin 90

0

, а

r1 r sin 90

0

,

то

Оскільки r

r

можна представити

у

вигляді

цей

r

r1 . Перетворимо

вираз використавши формулу для подвійного векторного добутку:

C ( r1) r1 r1 .

Якщо

розкрити

скалярні

добутки,

то

отримаємо

cos90

0

0 ,

cos0

0

2

, тобто

r1

r

2

, а модуль відцентрової сили

C

2

2

r1 .

C

r1

r1

Задача № 3.

Умова. Частинка одиничної маси на широті 600 рухається вздовж меридіану на південь з швидкістю 15 м/с. Розрахувати модуль та указати напрямок сили Коріоліса.

	Розв’язання задачі.
	Модуль					сили	Коріоліса	розрахуємо	за		формулою
	2						кут між	векторами	та		складає
K				V	sin , V ,					V
900 900					900		900 600 1200 (рис. 3.7).

71

Звідси маємо:

K 2 7.29 10 5 c 1 15 м с 1 sin1200 1.9 10 3 м с 2 .

Вектор сили Коріоліса є колінеарним осі x , тому що вектори та V лежать в площині YOZ , а їх векторний добуток повинен бути перпендикулярним площині, в якій вони лежать, а перпендикулярною є саме ось x . Якщо дивитись з кінця осі x , то поворот від вектора до

вектора V відбуватиметься проти годинникової стрілки, оскільки сила

Коріоліса дорівнює від’ємному подвійному векторному добутку та V , то міняємо напрямок на протилежний. Таким чином, сила Коріоліса буде спрямована уздовж кола широти зі сходу на захід.

Рисунок 3.7. – До визначення модуля та напрямку сили Коріоліса

Задача № 4.

Умова. Знайти проекції сили Коріоліса стандартної системи координат (вісь OX спрямована вздовж паралелі на схід, вісь OY – вздовж меридіана на північ, OZ – в зеніт), якщо на широті складові вектора

швидкості частинки одиничної маси дорівнюють відповідно u , , w , а кутова швидкість обертання Землі позначена .

Розв’язання задачі.
Вираз для сили Коріоліса має наступний вигляд: 2 V . Тобто, щоб
знайти	проекції сили Коріоліса,	необхідно знайти векторний добуток
		через їх проекції. Позначимо проекції
V ,	виразивши вектори та V
вектору як x , y та z . Тоді матимемо:

72