Geofizichna_gidrodinamika_statsionar

Очевидно, що згідно з теоремою Стокса, криволінійний інтеграл по замкненому контуру можна перетворити через подвійний інтеграл по поверхні, обмеженій цим контуром. У загальному випадку

C (Vdl ) (udx vdy wdz) ( n)dA,

l

l

А

x cos( n,x ) y cos( n, y ) z cos( n,z ) dA

n dA,

(2.36)

A

A

де

i

j

k

x

y

z

(2.37)

V

xi

y j

z k

u

v

w

- вихор швидкості, а

w			v	,		u		w	,
x	y				y	z
			z					x

	v		u
z	x				(2.38)
			y

- його складові. Підінтегральний вираз праворуч в (2.36) є скалярний добуток вектора вихора швидкості на одиничний вектор нормалі до поверхні А. Таким чином, циркуляція швидкості по будь-якому замкненому контуру дорівнює потоку вихора швидкості крізь довільну поверхню, проведену через цей контур.

Отже, кількісною характеристикою обертальної здатності поля швидкості в даній точці, через яку проходить задана площина з нормаллю n , може служити щільність циркуляції, яка дорівнює межі відношення циркуляції швидкості по замкненому контуру до площі обмеженої цим контуром:

(Vdl )

lim l A cos(n, ) . (2.39)

A 0

Відзначимо, що якщо рух повітря безвихровий, це означає, що циркуляція швидкості дорівнює нулю:

C (Vdl ) udx vdy wdz ( n )dA 0			(2.40)
l	l	А

53

Щоб з'ясувати фізичний зміст вихору швидкості, розглянемо елементарний об єм рідини або газу. Радіус-вектор r будь-якої точки об єму відносно початку координат буде мати проекції на координатні осі x, y, z. Нехай виділений об єм обертається відносно початку координат з кутовою швидкістю . Тоді лінійна швидкість руху будь-якої точки виділеного об′єму буде дорівнювати векторному добутку

V [ r ].

(2.41)

Проекції останнього рівняння на осі координат є складові лінійної швидкості, тобто

u y z z y
v z x x z .	(2.42)
w x y y x

Тоді, використовуючи ці вирази, знайдемо проекції складових вихору

x (	w			v ) x x 2 x ,
	y			z
y (	u	w) y y 2 y ,			(2.43)
	z			x
z (	v			u ) z z 2 z .
	x
				y

Отже,

	(2.44)
2

Таким чином, вихор швидкості дорівнює подвоєній кутовій швидкості обертання частинок рідини або газу і є характеристикою обертальної здатності поля швидкості в даній точці.

54

У метеорології та океанології найчастіше розглядається вертикальна складова вихору швидкості, що виражає вихрові властивості горизонтального поля вітру або течій.

Такого ж висновку можна дійти, якщо розглянути твердий диск радіуса r, що обертається з кутовою швидкістю . Згідно з визначенням знайдемо вираз для циркуляції та вихору:

L 2 r,vl r. C 2 r r 2 r 2 .qn C		2 r 2	2 .
A		r 2

При обертанні твердого тіла навколо миттєвої осі вихор дорівнює подвоєній кутовій швидкості обертання.

2.5.1 Рекомендації по вивченню теми

В результаті вивчення цієї теми студент повинен звернути увагу на такі базові знання та вміння: поняття циркуляції швидкості, теорема Стокса, зв’язок циркуляції швидкості з вихором швидкості, циркуляція в циклоні та антициклоні.

Для більш детального вивчення цих питань рекомендується використовувати наступну літературу: [4] – стор. 62–69, [11] – стор. 48–54

2.5.2 Приклад розв’язання типової задачі

Умова задачі. Обчислити циркуляцію швидкості по контуру ABCD, який є прямокутником із сторонами, паралельними координатним осям Ох і Оу і рівними заданим числам а і b (див. рисунок). Складові вектора

швидкості частинок рідини виражаються формулами: u 0, v nx, w 0.

55

Розв’язання задачі.

Для визначення циркуляції швидкості звернемося до відомої формули:

C	udx vdy wdz .
	ABCD

Оскільки дві з трьох складових швидкості дорівнюють нулю, згідно умовам задачі, то вихідну формулу представимо у вигляді:

C	vdy n	xdy ,
	ABCD	ABCD

і далі розіб'ємо вихідний інтеграл на чотири інтеграли, уздовж кожної із сторін прямокутника:

		B	C	D	A
C n	xdy n[		xdy	xdy	xdy xdy ] .
	ABCD	A	B	C	D

Оскільки інтеграли уздовж сторін АВ і CD дорівнюють нулю (координата у не змінюється), то робоча формула приймає вигляд:

		C	A
C n	xdy n[		xdy xdy ].
	ABCD	B	D

Обчислимо два визначених інтеграли з урахуванням координат.

C		yo b						yo b (xo a)(yo b yo ) (xo a)b.
xdy		(xo	a) dy (xo a)y
B		yo						yo
		A	y
		xdy		oxo dy xo y			yyoo b xo ( yo b yo ) xob.
		D	yo b
Остаточно маємо:
				C	A
		C n	xdy n[		xdy xdy ] n[(xo a)b xob] n ab .
			ABCD	B	D

56

Перевірка правильності отриманого розв’язку. З цією метою скористаємося теоремою Стокса:

C S z ,

де S - площа прямокутника ABCD, яка дорівнює добутку довжин сторін

	прямокутника (ab), z			v			u	- вертикальна складова вихору.
				x
							y
	Підставимо значення складових швидкості у вираз для вертикальної
	складової вихору: z		v			n . Остаточно маємо: C S z ab) n nab .
			x

Отже, задачу розв’язано правильно.

2.5.3Контрольні питання по темі

1.Сформулюйте теорему Стокса для циркуляції швидкості.

2.Сформулюйте теорему Томсона про циркуляцію для поверхні, обмеженої замкнутої кривої.

3.Що таке орієнтація кривої?

4.Дайте визначення циркуляції швидкості.

5.Вкажіть фізичне значення вихору швидкості.

6.По розподілу швидкості уздовж довільного контуру можна знайти циркуляцію швидкості. Чи можлива зворотна дія?

2.5.4Задачі для самостійного розв’язання

1.Обчислити циркуляцію швидкості за контуром ABCD, що представляє собою прямокутник зі сторонами, паралельними координатним осям Ох, Оy та рівними заданим числам а і b. Складові

вектора швидкості частинок рідини визначаються формулами:

Vx = 2my, Vy = y, Vz = 0, де m – константа.

2. Обчислити циркуляцію швидкості за контуром ABCD, що представляє собою прямокутник зі сторонами, паралельними координатним осям Ох, Оy та рівними заданим числам а і b. Складові вектора швидкості частинок рідини визначаються формулами: Vx = mxy, Vy = 0, Vz = 0 , де m – константа.

3. Обчислити циркуляцію швидкості за контуром ABCD, що представляє собою прямокутник зі сторонами, паралельними координатним осям Ох, Оy та рівними заданим числам а і b. Складові

57

вектора швидкості частинок рідини визначаються формулами: Vx =-my, Vy =-mx, Vz = 0 , де m – константа.

4. Обчислити циркуляцію швидкості за контуром ABCD, що представляє собою прямокутник зі сторонами, паралельними координатним осям Ох, Оy та рівними заданим числам а і b. Складові вектора швидкості частинок рідини визначаються формулами: Vx =-my, Vy = mx, Vz = 0 , де m – константа.

5. Обчислити циркуляцію швидкості за контуром ABCD, що представляє собою прямокутник зі сторонами, паралельними координатним осям Ох, Оy та рівними заданим числам а і b. Складові вектора швидкості частинок рідини визначаються формулами: Vx =-m, Vy =-my, Vz = 0, де m – константа.

6. Обчислити циркуляцію швидкості за контуром ABCD, що представляє собою прямокутник зі сторонами, паралельними координатним осям Ох, Оy та рівними заданим числам а і b. Складові вектора швидкості частинок рідини визначаються формулами: Vx =-mx, Vy = m, Vz = 0 , де m – константа.

7. Обчислити циркуляцію швидкості за контуром ABCD, що представляє собою прямокутник зі сторонами, паралельними координатним осям Ох, Оy та рівними заданим числам а і b. Складові вектора швидкості частинок рідини визначаються формулами: Vx = m, Vy = my, Vz = 0, де m – константа.

8. Обчислити циркуляцію швидкості за контуром ABCD, що представляє собою прямокутник зі сторонами, паралельними координатним осям Ох, Оy та рівними заданим числам а і b. Складові вектора швидкості частинок рідини визначаються формулами: Vx =-m, Vy = m, Vz = 0, де m – константа.

9. Обчислити циркуляцію швидкості за контуром ABCD, що представляє собою прямокутник зі сторонами, паралельними координатним осям Ох, Оy та рівними заданим числам а і b. Складові вектора швидкості частинок рідини визначаються формулами: Vx =-mx, Vy = my, Vz = 0 , де m – константа.

10. Обчислити циркуляцію швидкості за контуром ABCD, що представляє собою прямокутник зі сторонами, паралельними координатним осям Ох, Оy та рівними заданим числам а і b. Складові вектора швидкості частинок рідини визначаються формулами: Vx =-mx, Vy = mx, Vz = 0 , де m – константа.

58

3 ДИНАМІКА ОБ’ЄКТІВ ГЕОФІЗИЧНОЇ ГІДРОДИНАМІКИ

3.1Динаміка ідеальної рідини в інерціальній (необертовій) системі відліку

Інерціальними системами відліку називаються ті системи, по відношенню до яких виконується закон інерції1. Можна дати і інше визначення інерціальним системам відліку. Це системи відліку, в яких є справедливими закони Ньютона.

З дуже великою мірою точності можна вважати, що такого роду системою є геліоцентрична система відліку, початок координат якої співпадає з центром інерції сонячної системи, а осі проведено у напрямку віддалених зірок.

Система відліку, що жорстко пов’язана з Землею (геоцентрична система відліку), є неінерціальною, головним чином, внаслідок добового обертання Землі. Розглядаючи інерціальну систему відліку, ми нехтуємо обертанням Землі.

Розглянемо динаміку ідеальної рідини, тобто будемо нехтувати взаємодією між молекулами рідини, тобто в’язкістю рідини, оскільки опис останньої не залежить від вибору системи відліку.

Рівняння руху є математичним виразом другого закону Ньютона для матеріального об’ємного елемента або матеріальної точки; в загальному вигляді воно запишеться таким чином:

	d mV	N
		Fi ,		(3.1)
	dt
		i 1

де m – маса елементу, V – його швидкість. У правій частині рівняння (3.1) стоїть сума всіх N сил, що діють на елемент об’єму рідини.

Для одиничної маси ( m 1)

	N		(3.2)
dV	Fi ,
dt	i 1

Розглянемо сили, які в основному визначають характер природних течій рідини в інерціальній системі відліку.

1 Тіло, на яке не діє жодної сили, знаходиться або у стані абсолютного спокою або прямолінійного та рівномірного руху.

59

3.1.1Сила земного притягання

Сила земного притягання є виявом всесвітнього закону тяжіння і математичний вираз для неї має наступний вигляд:

	G		Mm		r	,	(3.3)
	*		r2 r
де	– гравітаційна стала; M – маса Землі; m – маса тіла; r						– радіус–

вектор точки (початок координат співпадає з центром планети). Мінус у формулу введений у зв’язку з тим, що напрямок векторів G0 та r прямо

протилежний.

Тоді вираз для гравітаційної сили Землі, що діє на одиничну масу, приймає наступний вигляд:

G			M r
*	G				,	(3.4)
m	0		r2 r

де G0 –сила притягання, що діє на одиницю маси.

Сила гравітації, що діє на матеріальну точку або тіло, є потенціальною, тобто робота цієї сили при переміщенні точки (тіла) залежить тільки від початкового і кінцевого положення точки (тіла) у просторі.

Потенціальний характер сили притягання дозволяє запровадити

скалярний параметр гравітаційного поля – потенціал	s	M	, який
зв’язаний з G0 співвідношенням:		r
G0 s grad s .			(3.5)

3.1.2Сила баричного градієнту

Виділимо у рідині нескінченно малий об’єм, V x y z , як

показано на рис. 3.1. Завдяки хаотичному руху молекул, імпульс (кількість руху) передається до стінок об’єму крізь навколишню рідину (рис. 3.1). Ця кількість руху, що передається за одиницю часу на одиницю площі, є просто тиск, який здійснюється навколишнім середовищем на стінки елементарного об’єму. Якщо тиск в центрі об’єму позначити через p0 , тоді

60

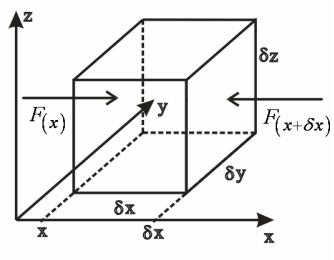
тиск на стінку площиною		y z	з координатою x x	можна
представити рядом Тейлора:
p	p x	члени більшвисоких порядків,		(3.6)
0	x 2

Рисунок 3.1. – Вплив x –складової сили баричного градієнта на рідкий об’єм.

Нехтуючи членами більш високих порядків у виразі (3.6) силу тиску, що діє на рідкий елемент зі сторони y z , можна представити:

F				p		p x y z .	(3.7)
x x					0
						x 2
Аналогічно знаходимо силу, що діє на елемент зі сторони площиною
y z з координатою x
F			p		p x y z .		(3.8)
x			0		x
						2

Таким чином, складова сили тиску, що діє на об’єм вздовж осі x , складає

F p x y z .

(3.9)

x x

61

Звідси випливає, що сила є пропорційною похідній від тиску в напрямку дії сили, і називається силою баричного градієнта. Маса m для виділеного рідкого об’єму – це густина , помножена на об’єм:

m x y z . Таким чином, x – компонента сили баричного градієнта на одиницю масу має вигляд:

Fx		1	p .	(3.10)
m		x

Аналогічно, можна отримати y та z складові сили баричного градієнта на одиницю маси:

Fy		1 p			F		1 p
				та	z				.	(3.11)
m		y					z
					m

Таким чином, загальна сила баричного градієнту на одиницю маси:

	F		1	p .	(3.12)
	m
З урахуванням одержаних виразів для основних					сил рівняння

руху (3.2) для ідеальної рідини можна записати в інерціальній системі відліку наступним чином:

dV				1
	I				p s ,	(3.13)
	dt	I

	dV			- прискорення
де VI	– швидкість в інерціальній системі координат,	I
		dt	I

в інерціальній системі координат.

Рівняння (3.13) – це рівняння руху в формі Ейлера.

Сили, що діють на частинку рідини, можуть бути або масовими, або поверхневими. Масові сили впливають на кожний елемент частинки рідини, який знаходиться як всередині частинки, так і на поверхні, що її обмежує. Масова сила, що діє на частинку рідини, пропорційна її масі.

Поверхневі сили є наслідок взаємодії між окремими елементами частинки рідини. Фізично вони обумовлені молекулярною структурою рідини та мають малий радіус дії. Тому поверхневі сили, що діють на частинку рідини, прикладені тільки до тих елементів частинки, які лежать

62