Geofizichna_gidrodinamika_statsionar

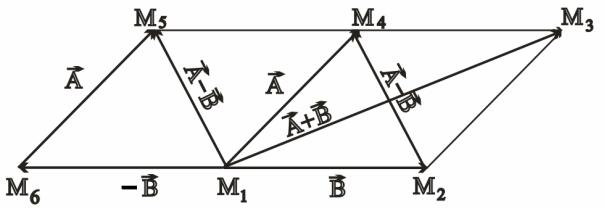
З рисунку 2.2 видно, що сумою двох векторів A та B є діагональ

паралелограма, який побудовано на векторах A і B .

Операція додавання має наступні властивості:

1. комутативність (переставність): A B B A

2. асоціативність (сполучність):

A

B

C

A

B

C

A

C B .

Перш ніж перейдемо до операції віднімання векторів, розглянемо

помноження вектора на скаляр.

Хай ми маємо вектор

A , що представлений відповідним відрізком.

Під добутком вектора A на скаляр

k розуміють такий вектор B , модуль

якого дорівнює

k

A

і який спрямований у той самий бік, що і A , якщо

k 0 , та у протилежний бік, якщо k 0.

З урахуванням

сказаного

вище, можна вважати, що операція

віднімання

вектора

B

від

вектора

A еквівалентна операції додавання

векторів A та B :

A B

A B .

Рисунок 2.3 – Віднімання векторів за правилом паралелограма

З рисунку	2.3 видно, що		для	того, щоб		відняти				від вектора	A
вектор B , треба побудувати вектор B , сполучити початки векторів A та
					M		M		є сумою векторів A
B і тоді діагональ M M паралелограма M M
	1	5		1 4		5		6
та B , тобто різницею A		B .
Звернемо увагу на те, що діагональ M1M5 , що є різницею A B ,
дорівнює діагоналі M2M4 паралелограма M1M2M3M4 , оскільки
паралелограми	M1M4M5M6		та	M1M2M3M4					є	рівними	за

побудовою (рис. 2.3).

13

Таким чином, в паралелограмі, що побудований на векторах A та B , одна діагональ представляє суму векторів A і B , а інша – їх різницю.

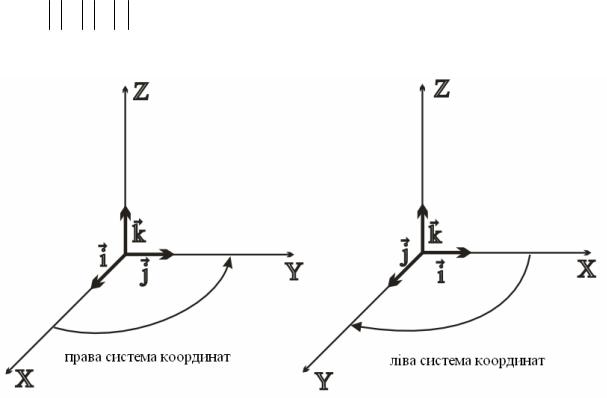
2.1.2Права та ліва системи координат

Прямокутна декартова система координат характеризується початком відліку (початком координат), напрямком осей координат та масштабом. Оберемо в якості початку відліку точку О, що жорстко пов’язана з тілом відліку. Додатний напрямок осей координат OX , OY , OZ задамо трьома

взаємно перпендикулярними спрямованими відрізками i , j , k (рис. 2.4). Хай i j k 1. Одиничні відрізки i , j , k утворюють систему одиничних векторів, або ортів прямокутної декартової системи координат.

Рисунок 2.4 – Зображення правої та лівої систем координат

Відрізняють два види прямокутних координатних систем, а саме: праву та ліву системи. В лівій системі (рис. 2.4) обертання від вісі OX по найкоротшій відстані до осі OY навколо осі OZ відбувається за годинниковою стрілкою, а в правій – проти годинникової стрілки. Якщо ми одночасно з обертанням від осі OX до осі OY будемо пересуватись уздовж вісі OZ , то отримаємо рух гвинта з лівою різзю у випадку лівої системи, і відповідно гвинта з правою різзю у випадку правої системи.

Ми користуватимемось в основному правою системою координат.

14

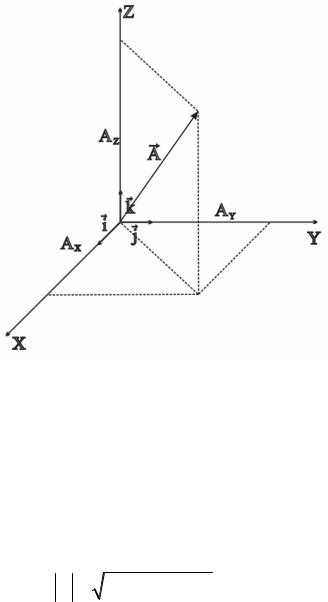
2.1.3Арифметизація алгебраїчних дій над векторами

До цього моменту ми незмінно пов’язували алгебраїчні операції над векторами з певними геометричними побудовами, що з практичної точки зору незручно.

Для здійснення арифметизації побудуємо вектор A з початком в точці О і проведемо через його кінець три площини, кожна з яких перпендикулярна одній з координатний осей. На осях відсікаються три взаємно перпендикулярних відрізка AX , AY , AZ (рис. 2.5).

				AZ AZ k ,
AX AX i		,	AY AY j ,		A AX i AY j AZk , (2.1)

Рисунок 2.5 – Розкладання вектора A на компоненти

Таким чином, у фіксованій системі координат вектор A однозначно визначається трійкою чисел AX , AY , AZ . Їх називають складовими або

координатами, або компонентами вектора A .
Довжину вектора A можна отримати, як діагональ прямокутного
паралелепіпеда, за теоремою Піфагора:
	AX2 AY2 A2Z ,
A		(2.2)

15

При додаванні (відніманні) двох векторів їх координати також додаються (віднімаються), а при помноженні вектора на число на це число помножуються всі компоненти вектора.

Якщо A AX i AY j AZk , а B BX i BY j BZk , то
C A B AX BX i AY BY j AZ BZ k .						(2.3)
		D kA kAX i kAY j kAZk .

2.1.4 Скалярний або внутрішній добуток двох векторів

Скалярним або внутрішнім добутком двох векторів A та B називають добуток довжин обох векторів, помножений на косинус кута між обома векторами.

Позначають скалярний добуток точкою, тобто

A B		A			B					(2.4)
							cos A,B ,
або ми можемо записати
						BA			AB ,
	A B		A					B		(2.5)

де BA – це проекція вектора B на вектор A , а AB – це проекція вектора A на вектор B .

В результаті скалярного добутку ми отримуємо скаляр.

Із визначення отримуємо, що скалярний добуток має наступні

властивості:

1. комутативність: A B B A ,

2. дистрибутивність (розподільність): A B C A

B

A C ,

3. асоціативність по

відношенню до числового

множника:

kA B A kB.

, якщо їх

Якщо A та B мають однаковий напрямок, то A B

A

B

та якщо A та

B ортогональні, то

напрямки протилежні, то A B

A

B

A B 0 .

16

Має	сенс розглянути		скалярний		добуток	ортів:	i i j j k k 1,
i j j k	k i 0 .
Скалярний добуток виражається через складові векторів наступним
чином:
	A B	AX i	AY j AZk BX i BY j BZk
			AXBX AYBY AZBZ ,				(2.6)

тобто скалярний добуток двох векторів дорівнює сумі добутків однойменних координат цих векторів.

2.1.5Векторний або зовнішній добуток двох векторів

Векторним або зовнішнім добутком двох векторів A та B називають вектор, який дорівнює за величиною площі паралелограма, побудованого

на векторах A і B , та є перпендикулярним площині цих векторів і спрямований таким чином, що, якщо дивитись з кінця цього вектора, то

обертання від A до B по найкоротшій відстані відбуватиметься у той самий бік, що і обертання від осі OX до осі OY навколо вісі OZ .

Векторний добуток позначається хрестиком, тобто C A B . Довжина вектора C за визначенням дорівнює

C		A		B		(2.7)
					sin A,B ,

З визначення векторного добутку зрозуміло, що напрямок вектора C залежить від вибору системи координат.

Якщо обрати праву систему координат, то потрібно обертати вісь OX навколо вісі OZ проти годинникової стрілки, щоб сумістити її з віссю OY .

Тому вектор C , що є векторним добутком векторів A і B , треба спрямувати таким чином, щоб, дивлячись з кінця вектору C , бачити

вектор A праворуч від B , тобто, щоб перехід від A до B по найкоротшій відстані відбувався проти годинникової стрілки (рис. 2.6).

Векторний добуток не має властивості комутативності. Якщо знаходити величину та напрямок вектора для векторного добутку B A , то

чисельне значення цього вектора буде таке саме, що і у випадку для A B за визначенням, а напрямок зміниться на протилежний (рис. 2.6), оскільки

17

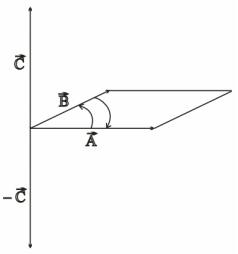
обертання вже відбуватиметься від вектора B до вектора A . Тобто

A B B A .

Рисунок 2.6. До впровадження поняття векторного добутку двох векторів

Векторний добуток має наступні властивості:

1. дистрибутивність: A B C A B A C

2. асоціативність

по

відношенню

до

числового

множника:

kA B A

kB .

Якщо

та

мають

однаковий

напрямок, або

їх

напрямки

A

B

, якщо

.

протилежні, то A B 0

A та B ортогональні, то A B

A

B

Важливо знати чому дорівнюють векторні добутки ортів. Оскільки вони утворюють ортонормовану систему трійки некомпланарних векторів, то (незалежно від того права система чи ліва):

i j k ,

j k i ,

k i j ,

j i k ,

k j i ,

i k j ,

i i j j k k 0 .

Скористувавшись властивостями векторного добутку та правилом перемноження ортів, отримаємо вираз векторного добутку:

A B AX i		AY j AZk BX i			BY j BZk

AYBXk AZBX j AXBYk AZBY i AXBZ j AYBZ i

18

AYBZ AZBY i AZBX AXBZ j AXBY AYBX k , (2.8)

В компактній формі це записують у вигляді визначника:

			i	j	k
A B			AX	AY	AZ		.	(2.9)
			BX	BY	BZ

Важливе застосування векторного добутку пов’язане з виразом для швидкості точок твердого тіла, яке обертається навколо своєї осі.

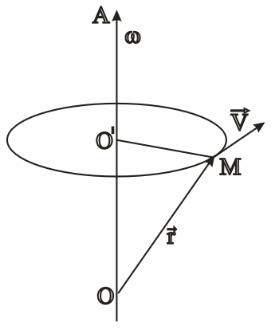
Рисунок 2.7 – Обертання твердого тіла навколо осі ОА.

Хай тверде тіло обертається навколо осі OA (рис. 2.7). Візьмемо будь–яку точку M твердого тіла; при обертанні твердого тіла ця точка описуватиме коло, що лежить у площині, яка перпендикулярна до осі обертання, та має свій центр O на осі обертання.

	За час t			та т. M		опише шлях
		радіус O M повернеться на кут
					O M
	O M , а швидкість т. M дорівнюватиме		V lim			O M та
					t
				t 0

буде спрямована перпендикулярно O M .

Величину lim називають кутовою швидкістю обертання тіла.

t 0 t

19

Відкладемо від т. O вектор , що дорівнює за величиною та спрямований уздовж OA у той бік, звідки обертання відбувається проти годинникової стрілки (для правої системи координат); назвемо цей вектор вектором кутової швидкості. Позначимо далі через r радіус–вектор т. M відносно якоїсь т. O осі обертання та складемо векторний добуток r .

Величина			його дорівнює		r sin AOM O M V , напрямок є
перпендикулярним до OA та OM та спрямований так само, як і V , так, що
дивлячись з кінця вектора				V , ми бачитимемо праворуч від r . Таким
чином,					як за величиною, так і за напрямком, тобто
			r співпадає з V
V	r .

2.1.6Рекомендації по вивченню теми

Вивчення положень геофізичної гідродинаміки передбачає оперування не тільки скалярними, але й векторними величинами. Тому студент повинен знати:

-властивості векторів;

-правила алгебраїчних дій над векторами; та вміти застосовувати ці правила на практиці.

Особливу увагу слід приділити поняттям «лівої» та «правої» систем координат, а також розкладанню векторів на компоненти та арифметизації дій над ними.

Для більш детального вивчення цих питань рекомендується використовувати наступну літературу: [2] – стор. 5–77, [9] – стор. 223–260.

2.1.7Приклади розв’язання типових задач

Задача № 1.

Умова. Задано вектори A 7, 6,6 та B 8,4, 8 . Знайти їх модулі, суму, різницю, скалярний та векторний добуток.

Пояснення до задачі. Запис A 7, 6,6 та B 8,4, 8 означає, що ми маємо справу з векторами, які можемо представити у наступному вигляді:

A 7i		6 j 6k		та B 8i		4 j 8k .

Розв’язання задачі.

Модулі векторів можна знайти за формулою (2.2):

			72 6	2	62		49 36 36	121 11,
A

20

Задача № 2.

			82 42 8	2		64 16 64	144 12 .
B

Для знаходження суми та різниці векторів A і B скористуємось формулою (2.3):

6 4

A B 7

8 i

j 6

8 k

15i

2 j

2k ,

6 4

A B 7

8 i

j 6

8 k i 10 j 14k .

Скалярний добуток визначимо за формулою (2.6):

24 48 16 .

A B 7 8 6 4 6 8 56

Для знаходження векторного добутку запишемо його через

визначник (2.9):

i

j

k

A B

7

6

6

8

4

8

6 8 6 4 i 7 8 6 8 j 7 4 6 8 k

24i 104 j 76k

Умова. Знайти скалярний та векторний добуток двох векторів A та B , якщо ці вектори лежать у площині XOY , а їх модулі дорівнюють 4 та 3

умовних одиниці відповідно, причому напрямок вектора A співпадає з

напрямком осі OY , а вектор B розташований під кутом 600 до вектора A (кут відраховується проти годинникової стрілки). Розглядається ліва декартова прямокутна система координат.

Розв’язання задачі.

Для знаходження скалярного добутку скористаємось формулою (2.4):

A B 4 3 cos 600 12 0.5 6 .

21

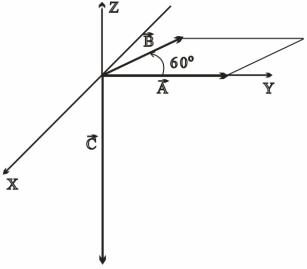
Щоб знайти модуль векторного добутку векторів A та B , скористуємось формулою (2.7). Вектор, що ми отримаємо в результаті

векторного добутку векторів A та B позначимо через C :
			4 3 sin 600 12 0.866 10.4.
		C
				та B знаходяться у площині XOY , то вектор							C
Оскільки вектори A
буде колінеарним осі OZ . Тепер треба визначитись тільки з тим, чи буде
його напрямок	співпадати з напрямком осі OZ ,					чи	–	ні.	Якщо		ми
дивитимемось з кінця осі OZ , то поворот від вектора										до	B
									A
відбуватиметься	проти			годинникової	стрілки,	та,		оскільки			ми
використовуємо ліву систему координат,					то поворот від		A	до	B	повинен
відбуватись за годинниковою стрілкою,					а для цього вектор C потрібно

спрямувати у напрямку протилежному осі OZ (дивись рисунок).

2.1.8Контрольні питання до теми

1.Яка величина називається скаляром?

2.Яка величина називається вектором?

3.Що таке модуль вектора? Як можна знайти цю величину?

4.Чим відрізняються права та ліва декартові системи координат?

5.Як можна додати один вектор до іншого, якщо задано їх довжини та напрямки? якщо задано їх координати?

6.Як можна відняти один вектор від іншого, якщо задано їх довжини та напрямки? якщо задано їх координати?

7.Дайте визначення для скалярного добутку двох векторів.

8.Перелічить властивості скалярного добутку.

22